
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
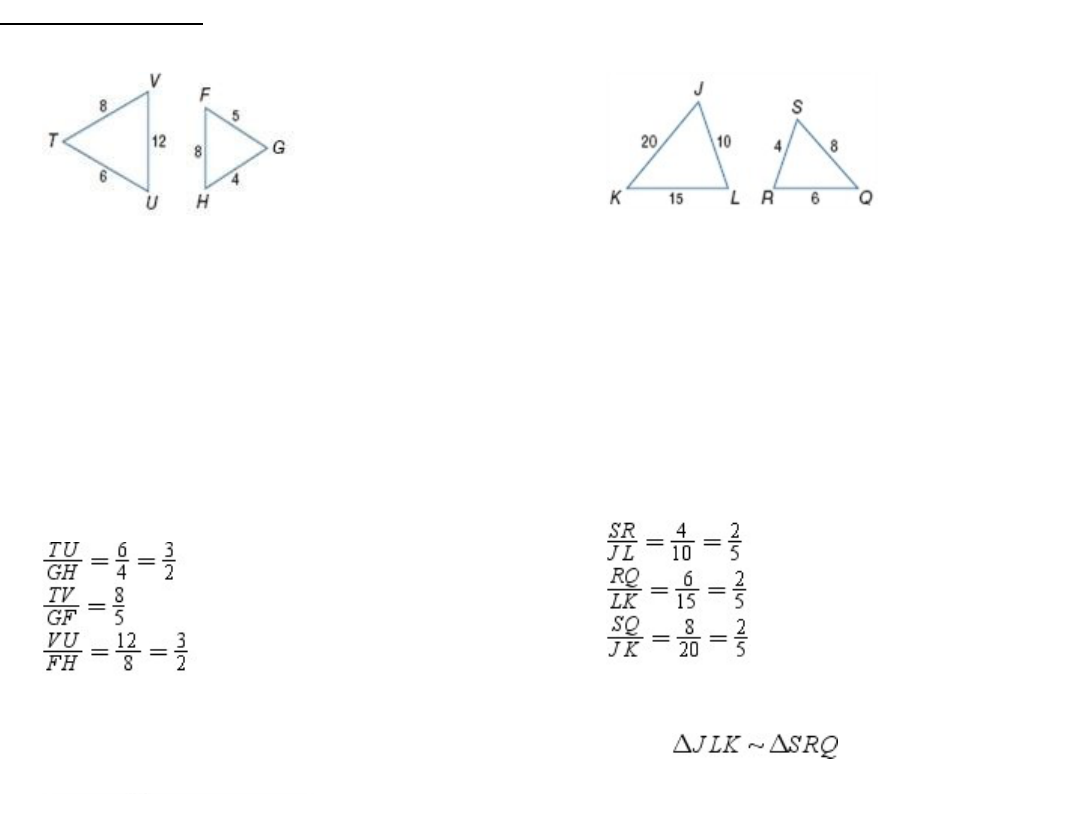
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage1
9-3 Similar Triangles
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage2
9-3 Similar Triangles
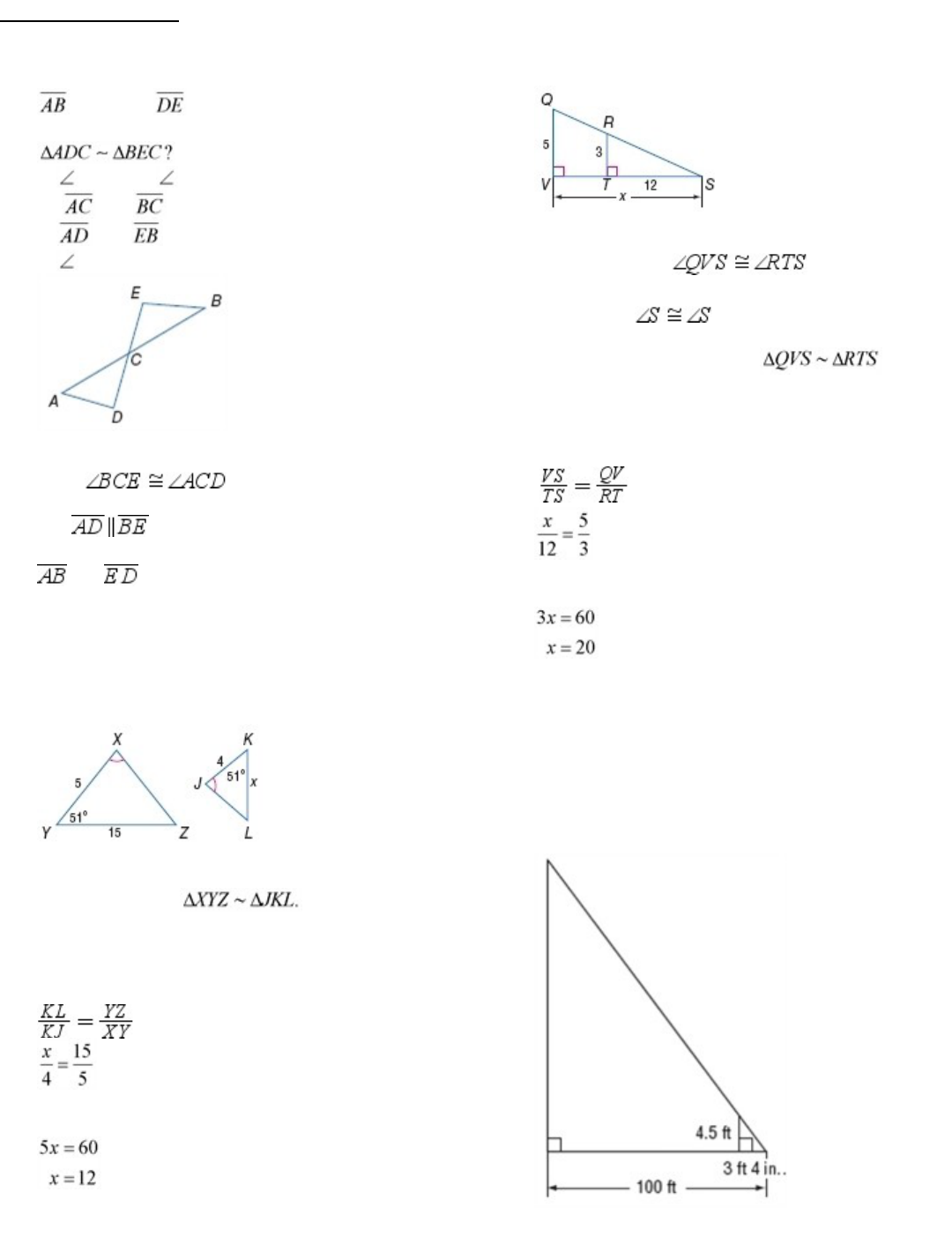
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage3
9-3 Similar Triangles
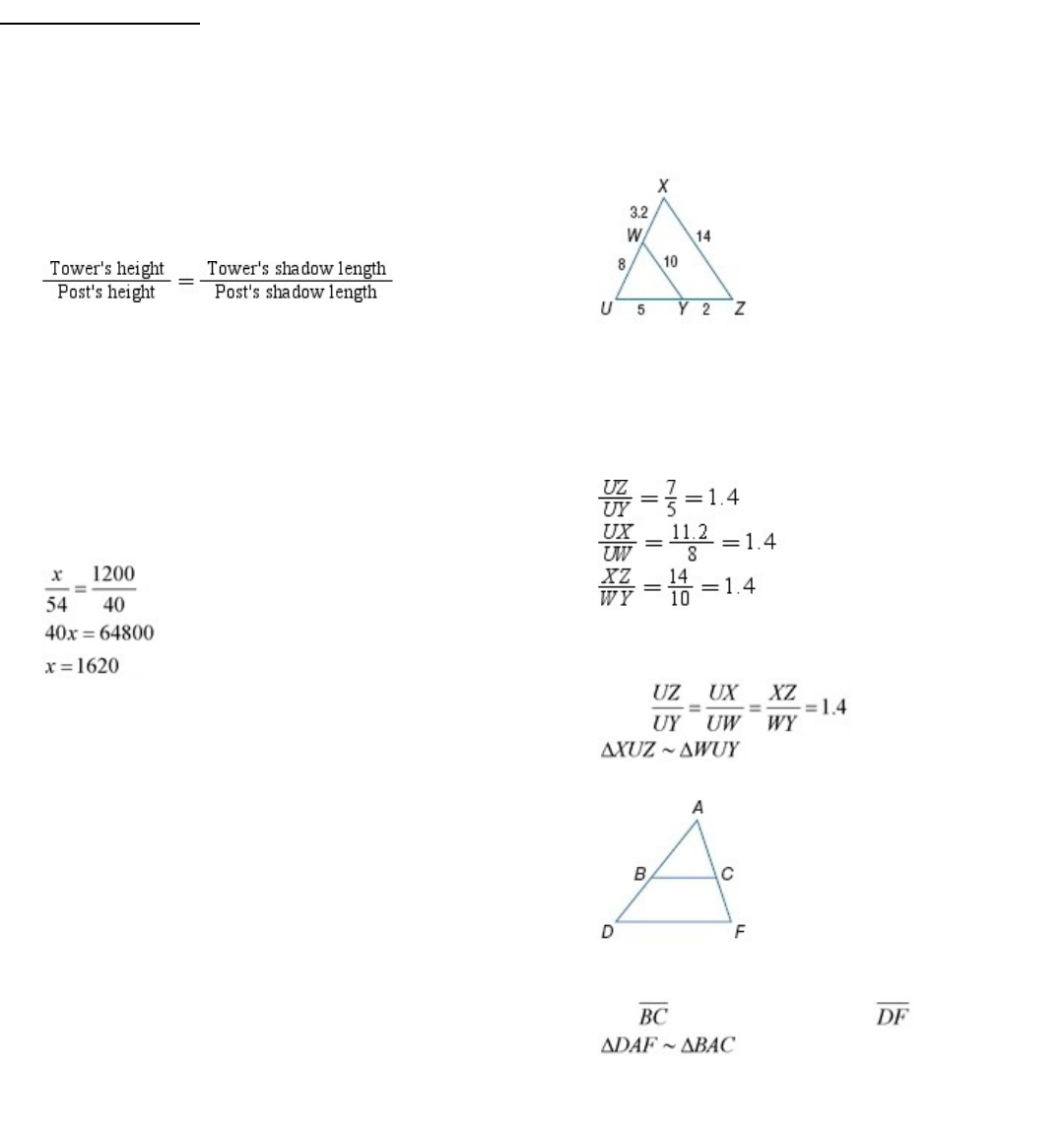
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage4
9-3 Similar Triangles
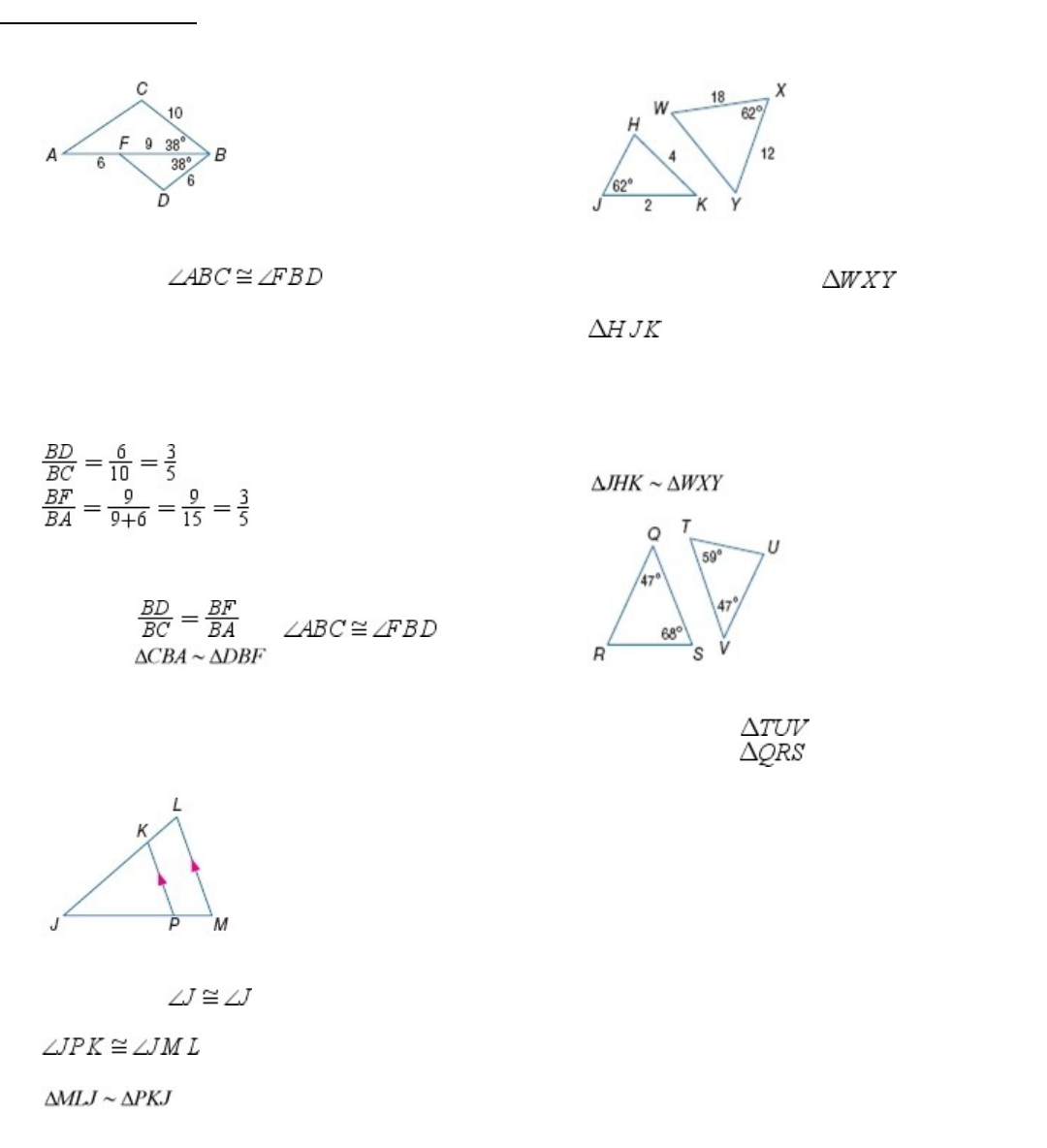
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage5
9-3 Similar Triangles
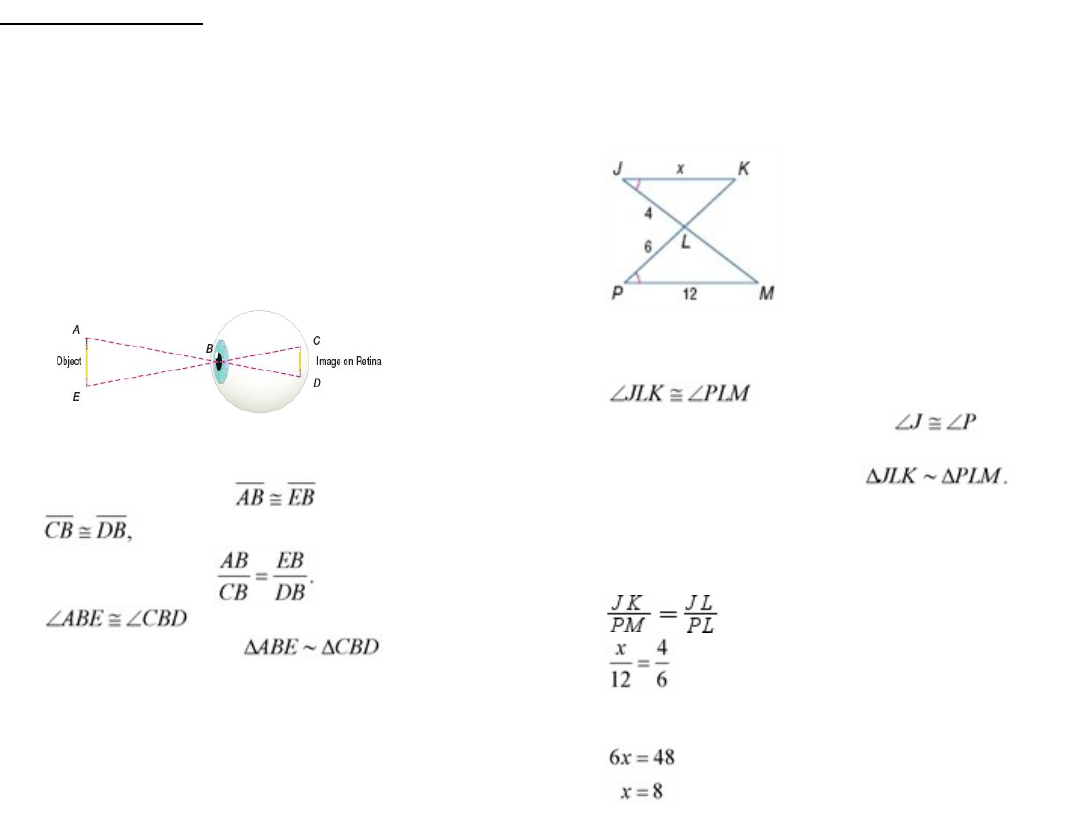
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage6
9-3 Similar Triangles
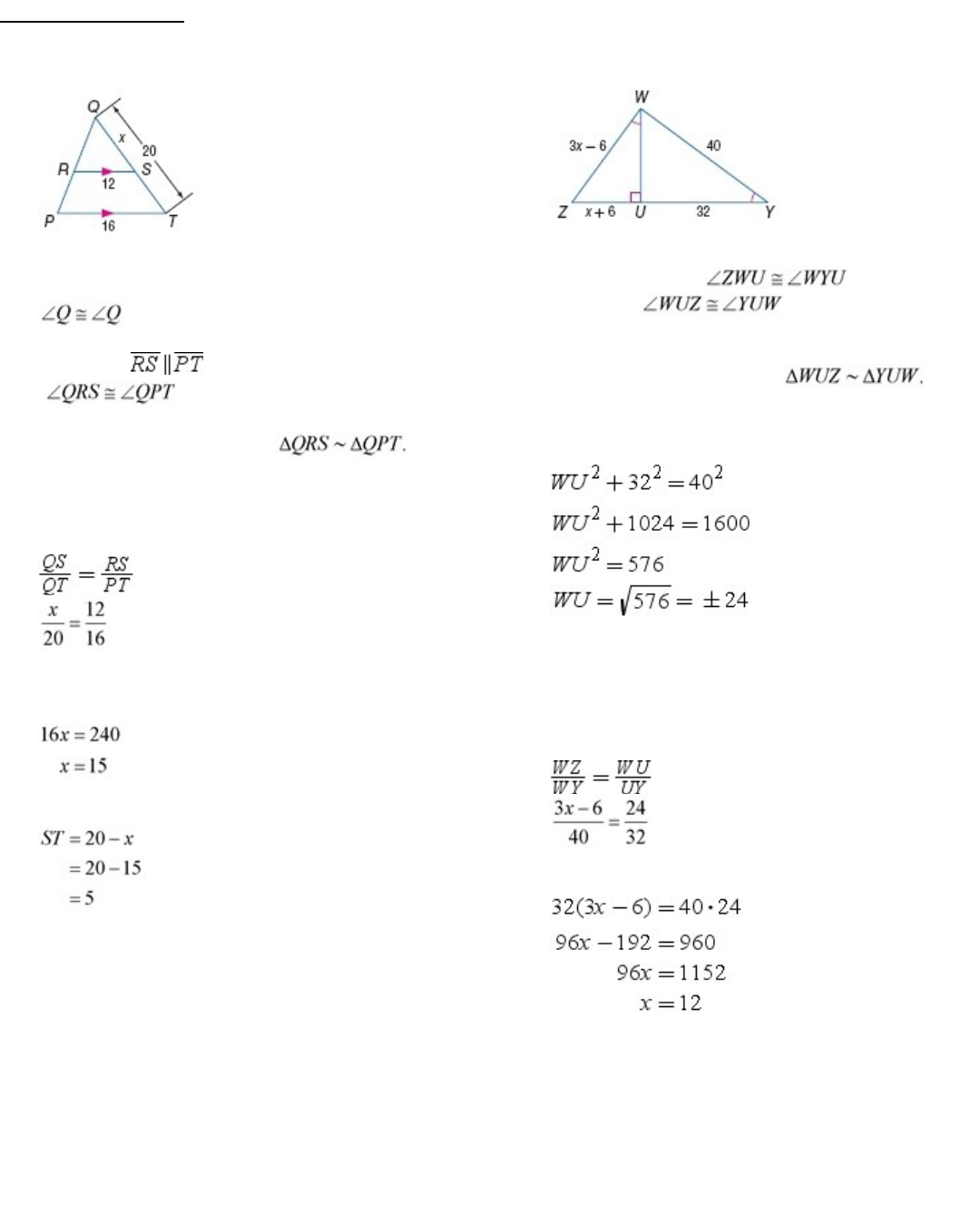
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage7
9-3 Similar Triangles
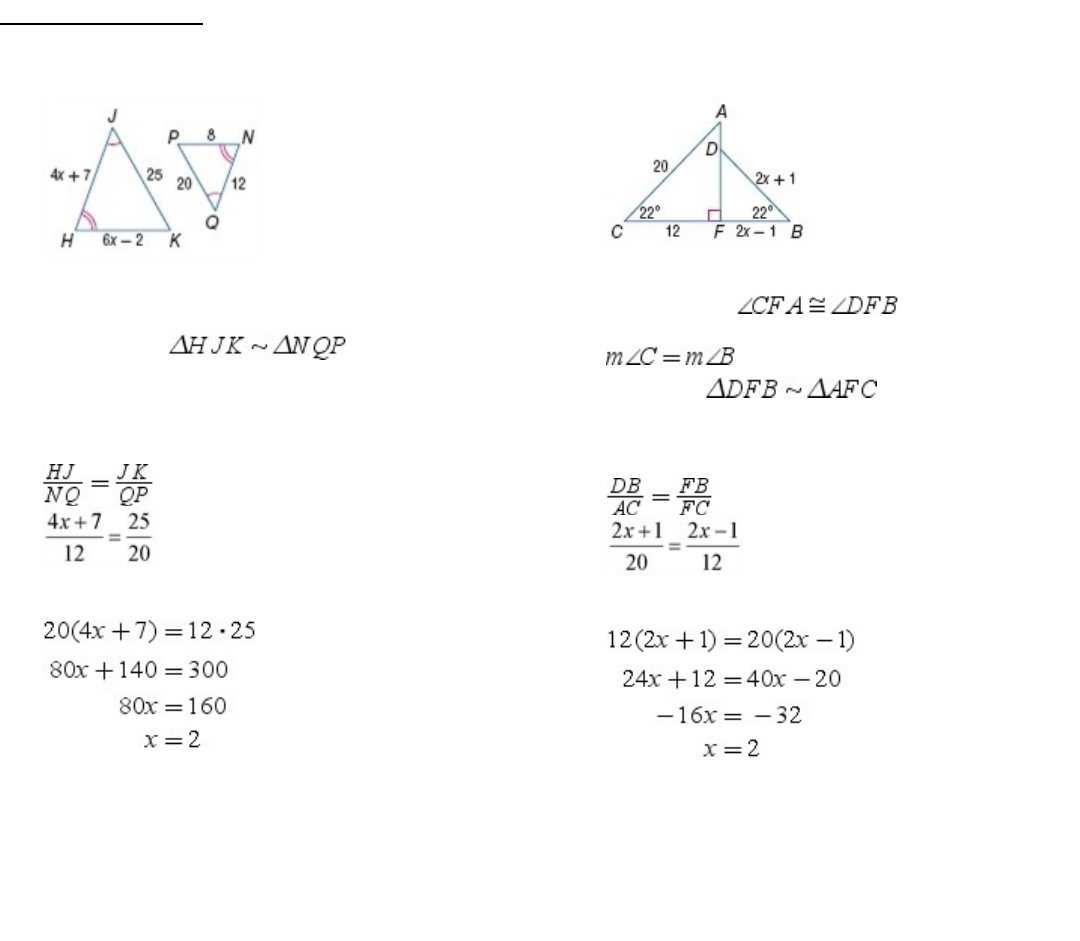
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage8
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage9
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage10
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage11
9-3 Similar Triangles
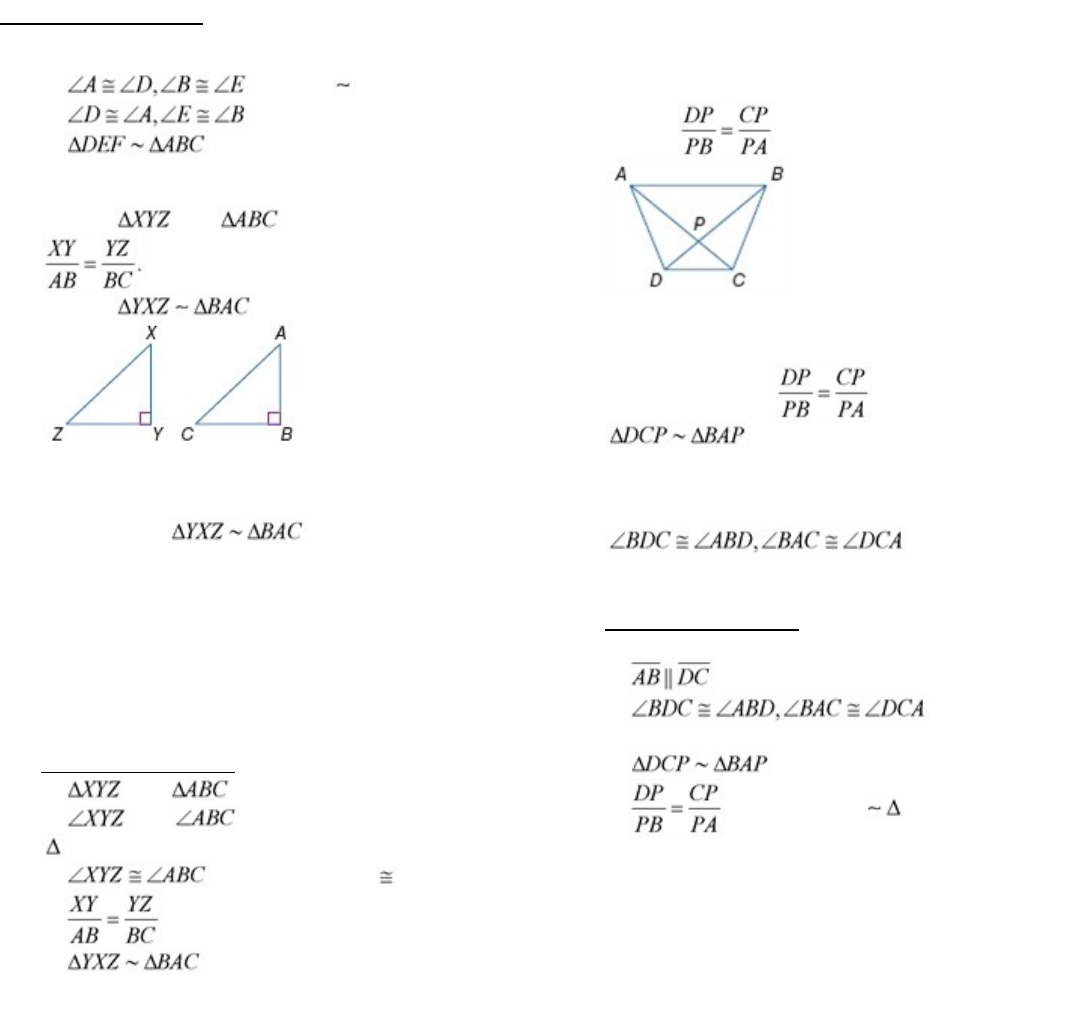
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage12
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage13
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage14
9-3 Similar Triangles
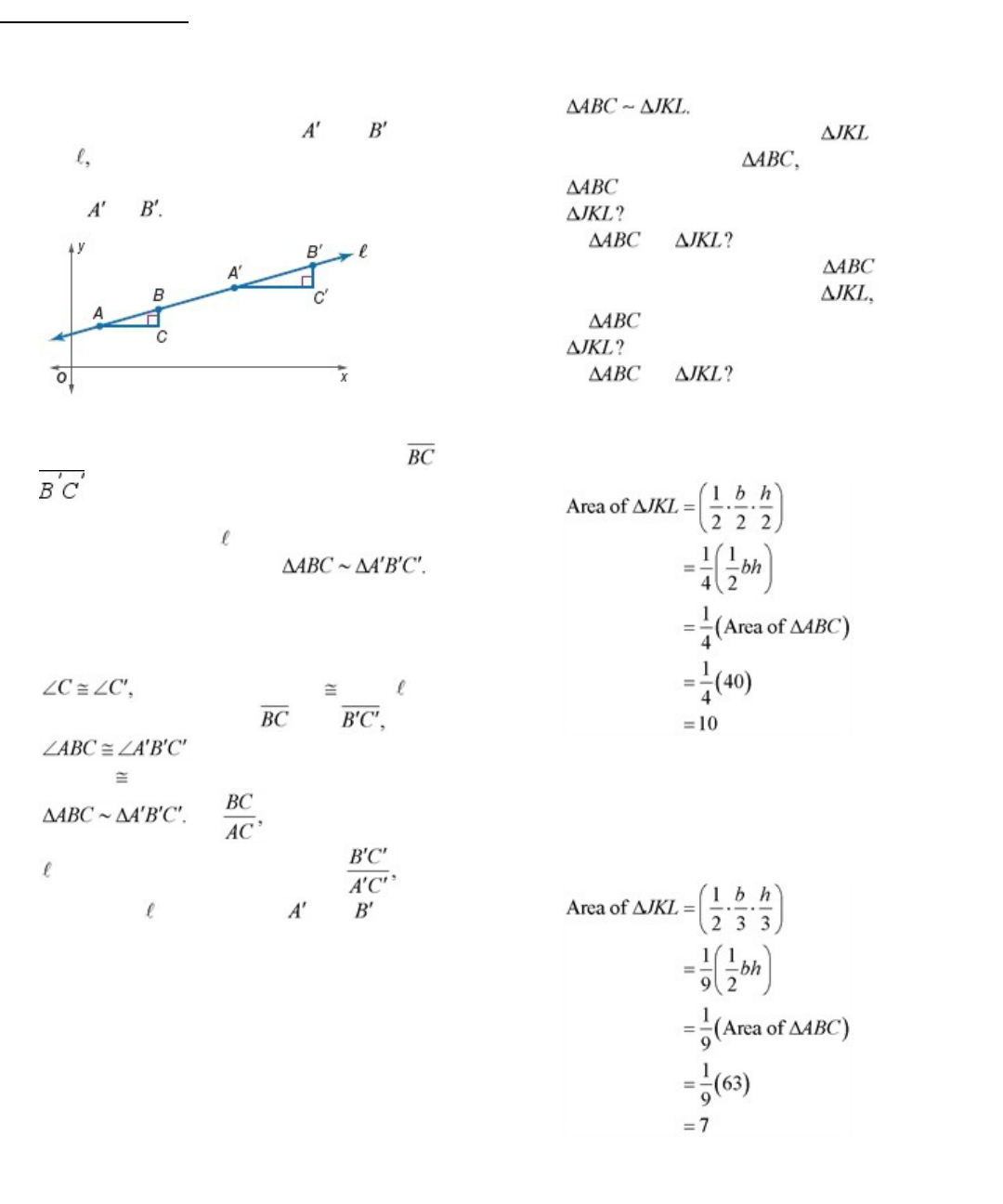
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage15
9-3 Similar Triangles
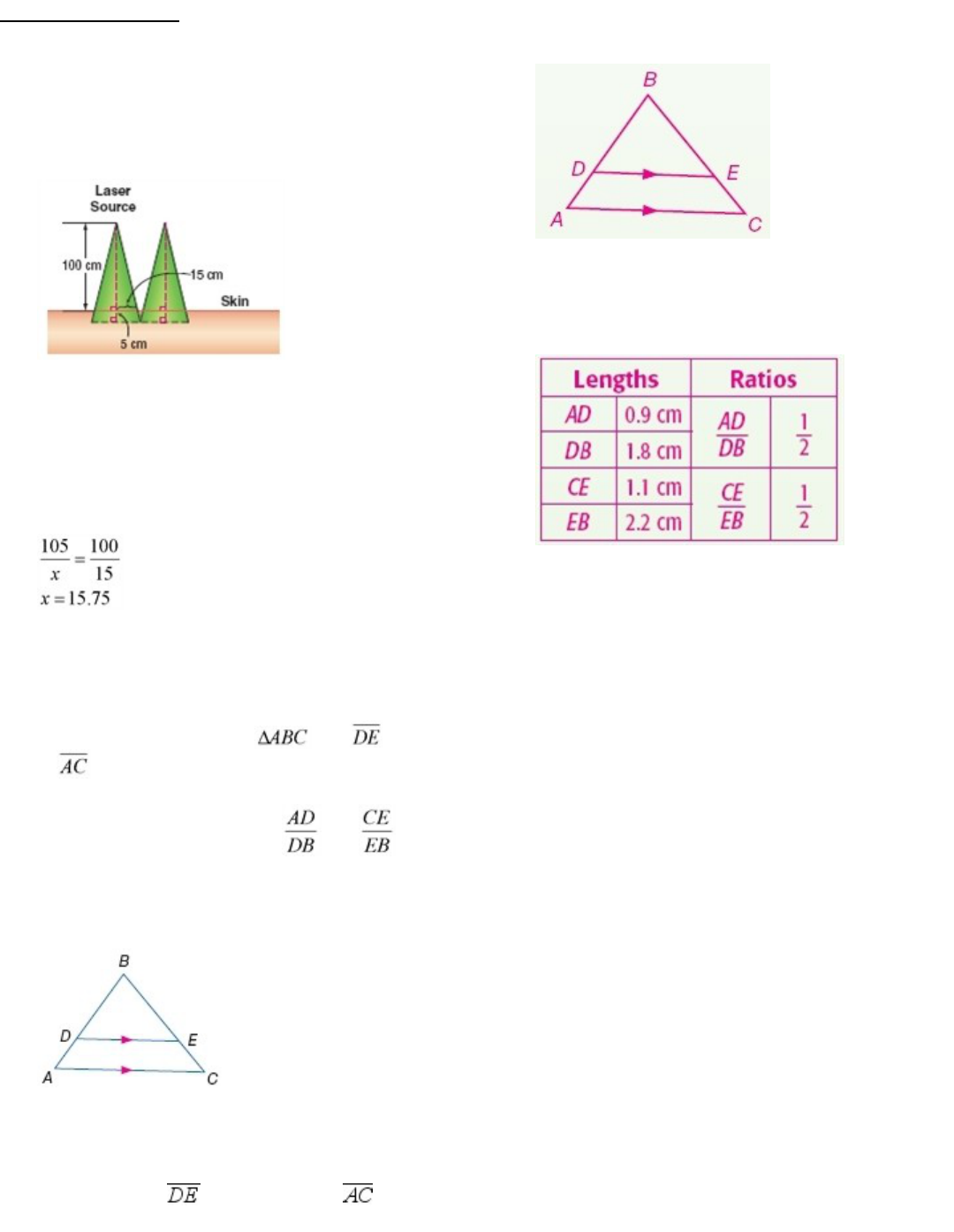
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage16
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage17
9-3 Similar Triangles
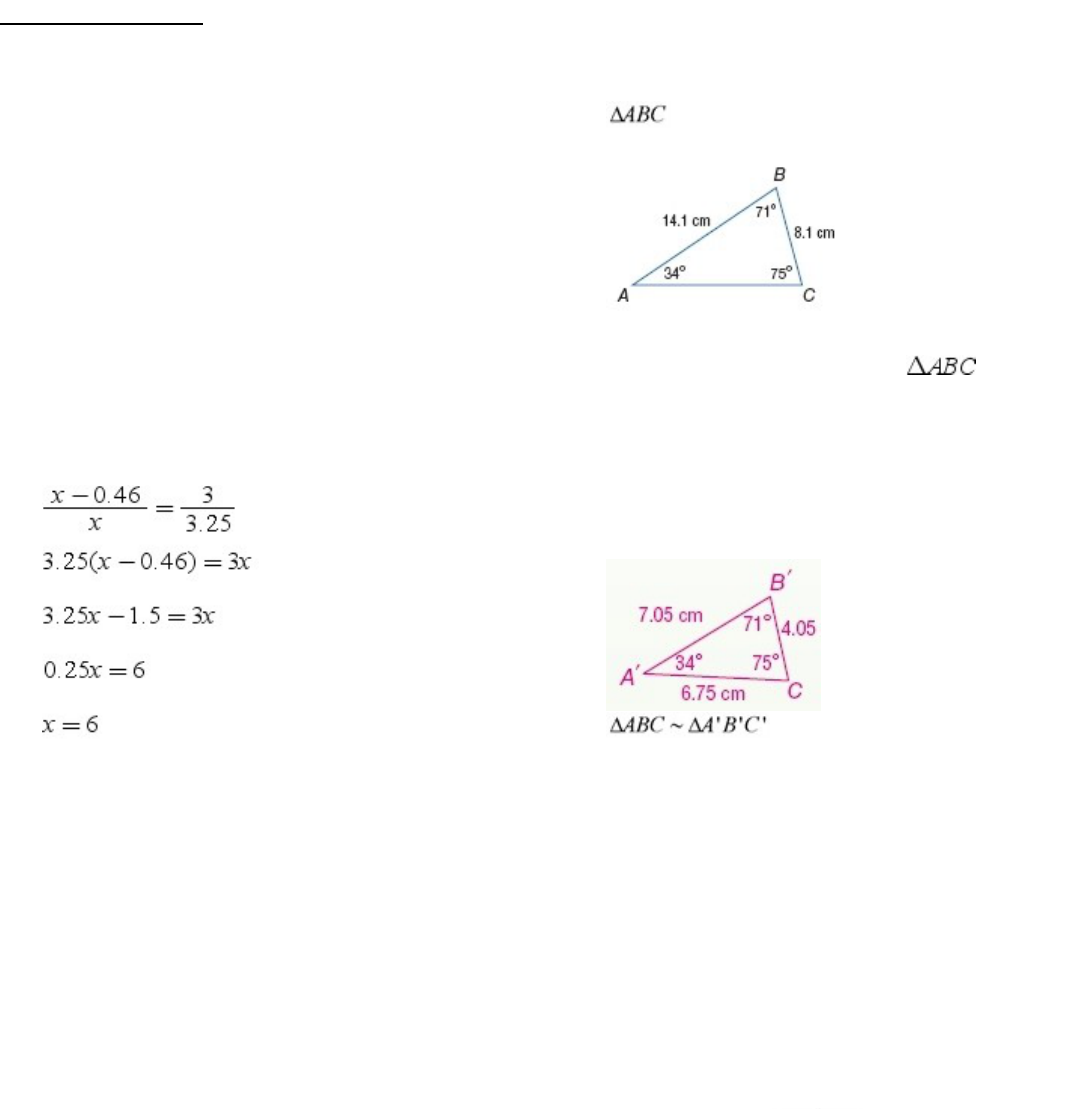
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage18
9-3 Similar Triangles
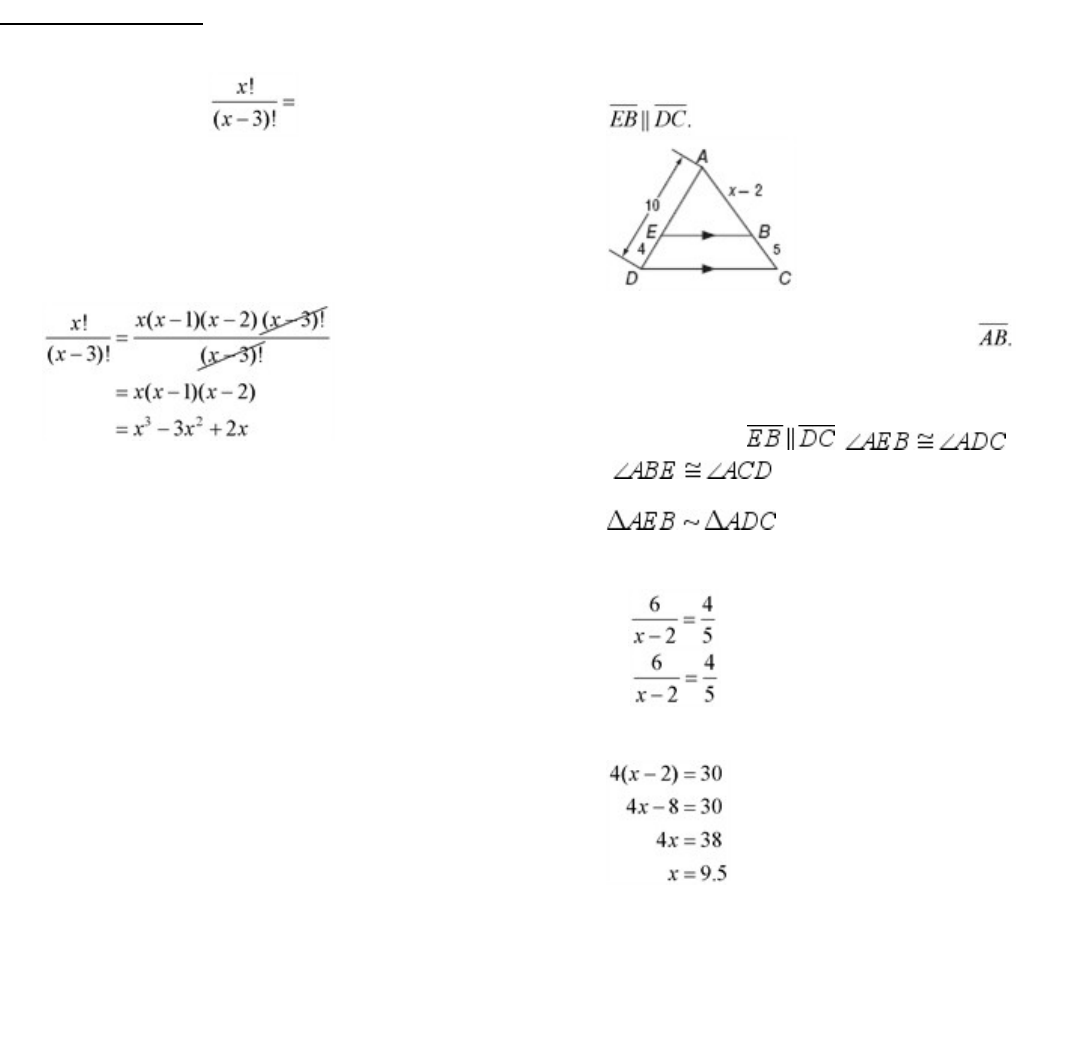
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage19
9-3 Similar Triangles
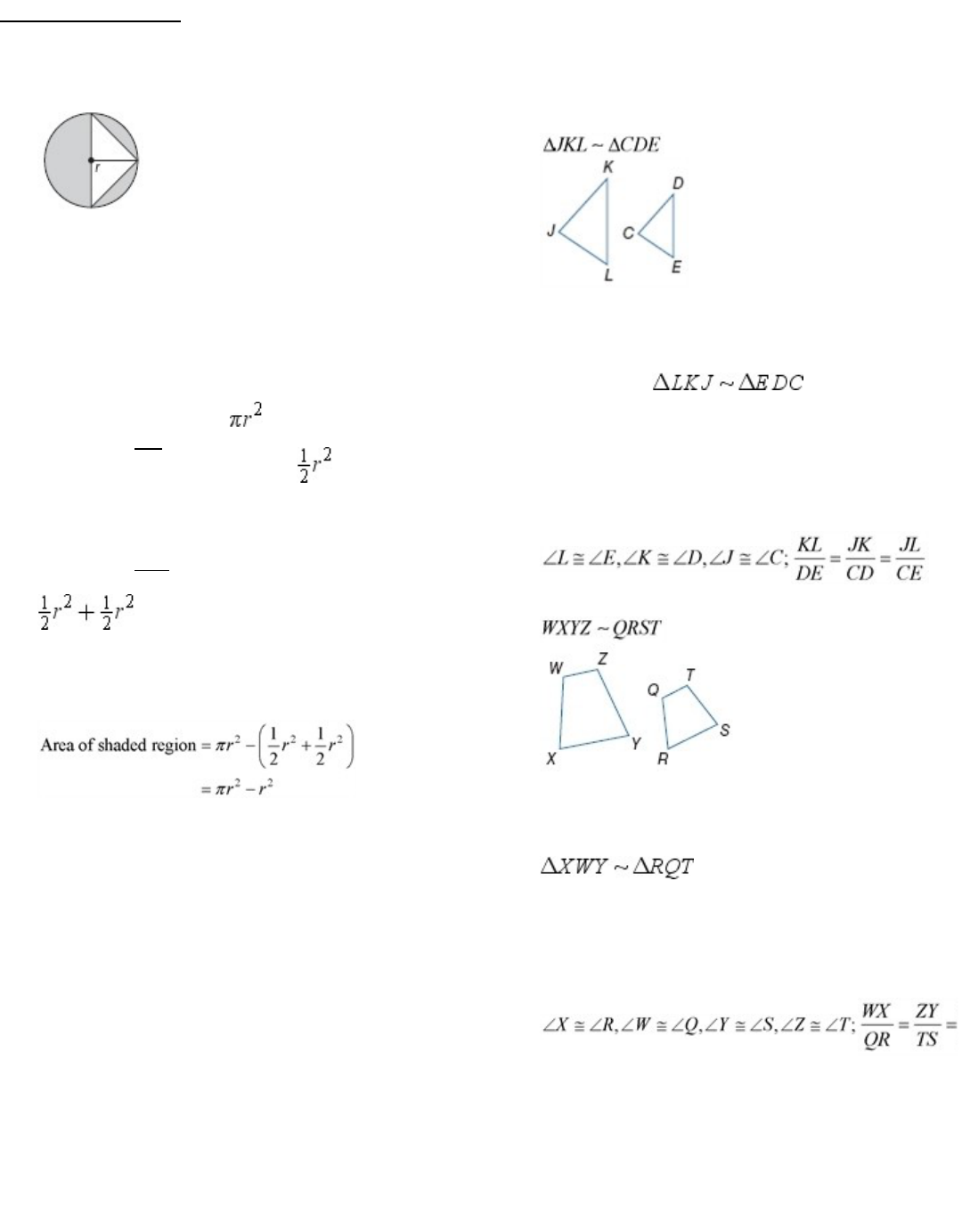
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage20
9-3 Similar Triangles
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage21
9-3 Similar Triangles

Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage22
9-3 Similar Triangles
Determine whether the triangles are similar. If
so, write a similarity statement. Explain your
reasoning.
1.
SOLUTION:
We can prove byAASimilarity.
1) We can prove that because
theyarealternateinterioranglesand
.(AlternateInteriorAnglesTheorem)
2)Wecanprovethat because
they are vertical angles. ( Vertical angles Theorem)
2.
SOLUTION:
We can prove bySASSimilarity.
1) We can prove that because they are
both right angles.(All right angles are congruent.)
2) Since these are right triangles, we can use the
PythagoreanTheoremtofindthemissingsides
Now, since we are using SAS Similarity to prove this
relationship, we can set up ratios of corresponding
sides to see if they are equal. We will match short
sidetoshortsideandmiddlesidetomiddleside.
So, bySASSimilarity.
3.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles can be
proven similar by using the SSS Similarity
Theorem.This requires that we determine if each pair
ofcorrespondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are not
allthesame,thesetrianglesarenotsimilar.
4.
SOLUTION:
Since no angles measures are provided in these
triangles, we can determine if these triangles are
similar by using the SSS Similarity Theorem.This
requires that we determine if each pair of
correspondingsideshaveanequalratio.
We know the following correspondences exist
because we are matching longest side to longest side,
middle to middle, and shortest to shortest:
Since the ratios of the corresponding sides are
equal, by SSS Similarity.
5.
MULTIPLE CHOICE
In the figure,
intersects atpointC. Which additional
information would be enough to prove that
A
DAC
and
ECB
are congruent.
B
and arecongruent.
C
and areparallel.
D
CBE
is a right angle.
SOLUTION:
Since , by the Vertical Angle
Theorem,optionCisthebestchoice.Ifweknow
that , then we know that the alternate
interior angles formed by these segments and sides
and are congruent. This would allow us to
useAASimilaritytoprovethetrianglesaresimilar.
CCSSSTRUCTUREIdentifythesimilar
triangles. Find each measure.
6.KL
SOLUTION:
By AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
7.VS
SOLUTION:
Wecanseethat because all right
trianglesarecongruent.
Additionally, ,byReflexiveProperty.
Therefore, by AA Similarity, .
Use the corresponding side lengths to write a
proportion.
Solve for x.
8.
COMMUNICATION
A cell phone tower casts a
100-foot shadow. At the same time, a 4-foot 6-inch
post near the tower casts a shadow of 3 feet 4
inches. Find the height of the tower.
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the tower’sheight.(Note that 1 foot = 12
inches and covert all the dimensions to inches)
100 ft = 1200 inches
4 feet 6 inches = 54 inches
3 feet 4 inches = 40 inches.
Substitute these corresponding values in the
proportion.
So, the cell phone tower is 1620 inches or 135 feet
tall.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
9.
SOLUTION:
Matching up short to short, middle to middle, and long
to long sides, we get the following ratios:
Since, then
bySSSSimilarity
10.
SOLUTION:
No; needstobeparallelto for
byAASimilarity.Additionally,there
are no given side lengths to compare to use SAS or
SSSSimilaritytheorems.
11.
SOLUTION:
We know that , because their
measures are equal. We also can match up the
adjacent sides that include this angle and determine if
they have the same ratio. We will match short to
shortandmiddletomiddlelengths.
Yes; since and , we
know that bySASSimilarity.
Determine whether the triangles are similar. If
so, write a similarity statement. If not, what
would be sufficient to prove the triangles
similar? Explain your reasoning.
12.
SOLUTION:
We know that due to the Reflexive
property. Additionally, we can prove that
, because they are corresponding
anglesformedbyparallellines.Therefore,
byAASimilarity.
13.
SOLUTION:
The known information for relates to a SAS
relationship, whereas the known information for
is a SSA relationship. Since they are no the
same relationship, there is not enough information to
determineifthetrianglesaresimilar.
If JH = 3 or WY = 24, then all the sides would have
the same ratio and we could prove
bySSSSimilarity.
14.
SOLUTION:
No; the angles of are 59, 47, and 74 degrees
and the angles of are 47, 68, and 65 degrees.
Since the angles of these triangles won't ever be
congruent, so the triangles can never be similar.
15.
CCSS MODELING
When we look at an object, it
is projected on the retina through the pupil. The
distances from the pupil to the top and bottom of the
object are congruent and the distances from the pupil
to the top and bottom of the image on the retina are
congruent. Are the triangles formed between the
object and the pupil and the object and the image
similar? Explain your reasoning.
SOLUTION:
Yes; sample answer: and
therefore, we can state that their ratios
areproportional,or We also know that
becauseverticalanglesare
congruent. Therefore, bySAS
Similarity.
ALGEBRA Identify the similar triangles. Then
find each measure.
16.JK
SOLUTION:
We know that vertical angles are congruent. So,
.
Additionally,wearegiventhat .
.
Therefore, by AA Similarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
17.ST
SOLUTION:
By the Reflexive Property, we know that
.
.
Also, since , we know that
( Corresponding Angle Postulate).
Therefore,byAASimilarity,
Use the corresponding side lengths to write a
proportion.
Solve for x.
18.WZ, UZ
SOLUTION:
Wearegiventhat and we also
knowthat ( All right angles are
congruent.)
Therefore, by AA Similarity,
Use the Pythagorean Theorem to find WU.
Since the length must be positive, WU = 24.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 12 in WZ and UZ.
WZ
= 3x – 6
=3(12)– 6
=30
UZ
= x + 6
=12+6
=18
19.HJ, HK
SOLUTION:
Since we are given two pairs of congruent angles,
we know that , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in HJ and HK.
HJ
= 4(2) + 7
=15
HK
= 6(2) – 2
= 10
20.DB, CB
SOLUTION:
We know that ( All right angles
are congruent.) and we are given that
.
Therefore, , by AA Similarity.
Use the corresponding side lengths to write a
proportion.
Solve for x.
Substitute x = 2 in DB and CB.
DB
= 2(2) + 1
=5
CB
= 2 (2) – 1 + 12
=15
21.GD, DH
SOLUTION:
We know that ( Reflexive Property) and
are given .
Therefore, by AA Similarity.
Use the corresponding side lengths to write a
proportion:
Solve for x.
Substitute x=8inGD and DH.
GD
= 2 (8) – 2
=14
DH
= 2 (8) + 4
=20
22.
STATUES
Mei is standing next to a statue in the
park. If Mei is 5 feet tall, her shadow is 3 feet long,
and the statue’s shadow is feet long, how tall is
the statue?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Since two pairs of angles are congruent, the right
trianglesaresimilarbytheAASimilarityPostulate.
So, the following proportion can be written:
Let x be the statue’s height and substitute given
values into the proportion:
So, the statue's height is 17.5 feet tall.
23.
SPORTS
When Alonzo, who is tall,stands
next to a basketball goal, his shadow is long,and
the basketball goal’s shadow is long.About
how tall is the basketball goal?
SOLUTION:
Make a sketch of the situation. 4 feet 6 inches is
equivalent to 4.5 feet.
In shadow problems, you can assume that the angles
formed by the Sun’s rays with any two objects are
congruent and that the two objects form the sides of
two right triangles.
Sincetwopairsofanglesarecongruent,theright
triangles are similar by the AA Similarity Postulate.
So, the following proportion can be written:
Let x be the basketball goal’s height. We know that 1
ft=12in..Convertthegivenvaluestoinches.
Substitute.
24.
FORESTRY
A hypsometer, as shown, can be used
to estimate the height of a tree. Bartolo looks through
the straw to the top of the tree and obtains the
readings given. Find the height of the tree.
SOLUTION:
Triangle EFD in the hypsometer is similar to triangle
GHF.
Therefore, the height of the tree is (9 + 1.75) or
10.75 meters.
PROOF Write a two-column proof.
25.Theorem 9.3
SOLUTION:
A good way to approach this proof is to consider
how you can get by AA Similarity.
You already have one pair of congruent angles (
) , so you just need one more pair. This
can be accomplished by proving that
and choosing a pair of
corresponding angles as your CPCTC. To get those
triangles congruent, you will need to have proven that
but you have enough information in
the given statements to do this. Pay close attention to
how the parallel line statement can help. Once these
triangles are similar, you can create a proportion
statement and combine it with the given statements
to create the
relationship that .
Given: ,
Prove:
Proof:
Statements (Reasons)
1.
2. , (Corr. 's
Post.)
3. (Trans.Prop.)
4. (AASimilarity)
5.
6. AB·QP = AQ·BC; AB·EF = DE·BC (Cross
products)
7. QP = EF (Def. of segs.)
8. AB·EF = AQ·BC (Subst.)
9. AQ·BC = DE·BC (Subst.)
10. AQ = DE (Div. Prop.)
11.
12.
13. (CPCTC)
14. (Trans.Prop.)
15. (AASimilarity)
26.Theorem 9.4
SOLUTION:
This is a three-part proof, as you need to prove three
different relationships - that Reflexive, Symmetric,
and Transitive properties are true for similar
triangles. For each part of this proof, the key is to
find a way to get two pairs of congruent angles
which will allow you to use AA Similarity
Postulate.As you try these, remember that you
already know that these three properties already hold
for congruent triangles and can use these
relationshipsinyourproofs.
Reflexive Property of Similarity
Given:
Prove:
Proof:
Statements (Reasons)
1.
2. , (Refl.Propof .)
3. (AASimilarity)
Transitive Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of
polygons)
3. (Trans.Prop.)
4. (AASimilarity)
Symmetric Property of Similarity
Given:
Prove:
Statements (Reasons)
1.
2. (Def.of polygons)
3. (Symm.Propof.)
4. (AASimilarity)
PROOF Write a two-column proof.
27.
Given:
and arerighttriangles;
Prove:
SOLUTION:
The given information in this proof is almost all you
need to prove by SAS Similarity
theorem. You already have two pairs of proportional
corresponding sides. You just need to think about
how to get the included angles congruent to each
other.
Proof:
Statements (Reasons)
1. and arerighttriangles.(Given)
2. and arerightangles.(Def.ofrt.
)
3. (Allrt.anglesare .)
4. (Given)
5. (SASSimilarity)
28.
Given:
ABCD is a trapezoid.
Prove:
SOLUTION:
Think backwards when attempting this proof. In
order to prove that , we need to show that
. To prove triangles are similar, you
need to prove two pairs of corresponding angles are
congruent. Think about what you know about
trapezoids and how that can help you get
.
Proof:
Statements (Reasons)
1. ABCD is a trapezoid. (Given)
2. (Def.oftrap.)
3. (Alt.Int.angle
Thm.)
4. (AASimilarity)
5. (Corr.sidesof s are proportional.)
29.
CCSS MODELING
When Luis’s dad threw a
bounce pass to him, the angles formed by the
basketball’s path were congruent. The ball landed
ofthewaybetweenthembeforeitbouncedback
up. If Luis’s dad released the ball 40 inches above
the floor, at what height did Luis catch the ball?
SOLUTION:
Since the ball landed ofthewaybetweenthem,
the horizontal line is in the ratio of 2:1.
By AA Similarity, the given two triangles are similar.
Form a proportion and solve for x. Assume that Luis
will catch the ball at a height of x inches.
So, Luis will catch the ball 20 inches above the floor.
COORDINATE GEOMETRY and
haveverticesX(–1, –9), Y(5, 3), Z(–1,
6), W(1, –5), and V(1, 5).
30.Graph the triangles, and prove that
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now, find the ratios of the corresponding sides:
Since by
SSS Similarity.
31.Find the ratio of the perimeters of the two triangles.
SOLUTION:
We can prove that by using the
distance formula to determine the lengths of each
side of the triangles. Then, we can set up ratios to
determine if the ratios of corresponding sides are
equal and use SSS Similarity theorem to prove the
trianglesaresimilar.
The lengths of the sides of are:
XY
=
YZ =
ZX = 6 – (–9)=15;
The lengths of the sides of are:
VW = 5 – (–5)=10;
WY =
YV =
Now,findtheperimeterofeachtriangle:
32.
BILLIARDS
When a ball is deflected off a smooth
surface, the angles formed by the path are
congruent. Booker hit the orange ball and it followed
the path from A to B to C as shown below. What
was the total distance traveled by the ball from the
time Booker hit it until it came to rest at the end of
the table?
SOLUTION:
By AA Similarity, the given triangles are similar.
FormaproportionandsolveforBC.Convertthe
fractions to decimals.
So, the total distance traveled by the ball is about 61
in..
33.
PROOF
Use similar triangles to show that the slope
of the line through any two points on that line is
constant. That is, if points A, B, and areon
line usesimilartrianglestoshowthattheslopeof
the line from A to B is equal to the slope of the line
from to
SOLUTION:
In this proof, it is important to recognize that and
are both vertical lines and are, therefore,
parallel to each other. Using this relationship, along
with the fact that line is a transversal of these
segments, we can prove that
Once this is proven, you can use a proportion
statementtocompletetheproof.
since all rt. angles are . Line isa
transversalof||segments and so
sincecorrespondinganglesof||
lines are . Therefore, by AA Similarity,
So theslopeofline
throughpointsA and B, is equal to the
slope of line throughpoints and .
34.
CHANGING DIMENSIONS
Assume that
a.
If the lengths of the sides of arehalfthe
length of the sides of andtheareaof
is40squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
b.
If the lengths of the sides of arethree
times the length of the sides of andthearea
of is63squareinches,whatistheareaof
Howisthearearelatedtothescalefactor
of to
SOLUTION:
a.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 10 square
inches.
The ratio of the areas is the square of the scale
factor.
b.
Let b and h be the base and height of the triangle
ABC respectively.
Thus, the area of the triangle JKL is 7 square inches.
The ratio of the areas is the cube of the scale factor.
35.
MEDICINE
Certain medical treatments involve
laser beams that contact and penetrate the skin,
forming similar triangles. Refer to the diagram. How
far apart should the laser sources be placed to ensure
that the areas treated by each source do not overlap?
SOLUTION:
For 100 cm, it covers an area that has a radius of 15
cm. It penetrates and go inside the skin for 5 cm. so,
the total height is 105 cm. Assume that for 105 cm,
laser source covers an area that has a radius of x
cm.
Form a proportion.
So, the laser beam covers 15.75 + 15.75 or 31.5 cm.
36.
MULTIPLE REPRESENTATIONS
In this
problem, you will explore proportional parts of
triangles.
a. GEOMETRIC
Draw a with
parallel
to
asshown.
b. TABULAR
Measure and record the lengths AD,
DB, CD, and EB and the ratios
and ina
table.
c. VERBAL
Make a conjecture about the segments
created by a line parallel to one side of a triangle and
intersecting the other two sides.
SOLUTION:
a.
The triangle you draw doesn't have to be
congruent to the one in the text. However, measure
carefully so that is parallel to side
.
Sampleanswer:
b.
When measuring the side lengths, it may be
easiest to use centimeters. Fill in the table with the
correspondingmeasures.
Sample answer:
c.
Observe patterns you notice in the table that are
formed by the ratios of sides of a triangle cut by a
parallelline.
Sample answer: The segments created by a line || to
onesideofatriangleandintersectingtheothertwo
sides are proportional.
37.
WRITING IN MATH
Compare and contrast the
AA Similarity Postulate, the SSS Similarity Theorem,
and the SAS similarity theorem.
SOLUTION:
Sample answer: The AA Similarity Postulate, SSS
Similarity Theorem, and SAS Similarity Theorem are
all tests that can be used to determine whether two
trianglesaresimilar.
The AA Similarity Postulate is used when two pairs
ofcongruentanglesoftwotrianglesaregiven.
The SSS Similarity Theorem is used when the
corresponding side lengths of two triangles are
given.
The SAS Similarity Theorem is used when two
proportional side lengths and the included angle of
two triangles are given.
38.
CHALLENGE
isanaltitudeof Find
YW.
SOLUTION:
Both
are isosceles right
triangles, so by AA Similarity postulate, we know
thattheyaresimilar.Thisallowsustosetupa
proportionofcorrespondingsidelengthstofindYW:
First,weneedtofindthelengthofXZ.
Now, substitute the side lengths you know into the
proportion .
Therefore, YW= .
39.
REASONING
A pair of similar triangles has angle
measuresof45°,50°,and85°.Thesidesofone
triangle measure 3, 3.25, and 4.23 units, and the sides
of the second triangle measure x
–
0.46, x, and x +
1.81 units. Find the value of x
.
SOLUTION:
Using the given information, sketch two triangles and
label the corresponding sides and angles. Make sure
you use the Angle- Sides relationships of triangles to
place the shortest sides across from the smallest
angles,etc.
Form a proportion and solve for x.
40.
OPEN ENDED
Draw a triangle that is similar to
shown.Explainhowyouknowthatitis
similar.
SOLUTION:
When making a triangle similar to , keep in
mind the relationships that exist between the angles
of similar triangles, as well as the sides. We know
that the corresponding sides of similar triangles are
proportional and the corresponding angles are
congruent.
Sample answer:
becausethemeasuresofeach
side are half the measure of the corresponding side
and the measures of corresponding angles are equal.
41.
WRITINGINMATH
How can you choose an
appropriate scale?
SOLUTION:
Sample answer: You could consider the amount of
space that the actual object occupies and compare it
to the amount of space that is
available for the scale model or drawing. Then, you
could determine the amount of detail that you want
the scale model or drawing to have, and you could
use these factors to choose an appropriate scale.
42.
PROBABILITY
A
3.0
B
0.33
C
x
2
–
3x + 2
D
x
3
–
3x
2
+ 2x
SOLUTION:
So, the correct option is D.
43.
EXTENDED RESPONSE
In the figure below,
a.
Write a proportion that could be used to find x.
b.
Find the value of x and the measure of
SOLUTION:
Since we know ,
and
because they are corresponding
anglesformedbyparallellines.Therefore,
and corresponding sides are
proportional.
a.
b.
Solve for x.
Substitute x = 9.5 in AB.
AB = x
–
2
= 9.5
–
2
= 7.5
44.
ALGEBRA
Which polynomial represents the area
of the shaded region?
F
π
r
2
G
π
r
2
+ r
2
H
π
r
2
+ r
J
π
r
2
–
r
2
SOLUTION:
The area of the circle is
.
The area of one white triangle is , because the
radius of the circle is both the height and the base of
thetriangle.
The area of two white triangles would be
.
To find the area of the shaded region, you can
subtract the area of the two white triangles from the
circle'sarea.
So, the correct option is J.
45.
SAT/ACT
The volume of a certain rectangular solid
is 16x cubic units. If the dimensions of the solid are
integers x, y, and z units, what is the greatest possible
value of z?
A
32
B
16
C
8
D
4
E 2
SOLUTION:
The volume of a rectangular solid with dimensions x,
y, and z is given by xyz. So xyz = 16. Since all
dimensions are integers, and since lengths must be
positive, the least possible value of x
and
y is 1. In
that case, z = 16. So the correct answer is B.
List all pairs of congruent angles, and write a
proportion that relates the corresponding sides
for each pair of similar polygons.
46.
SOLUTION:
The order of vertices in a similarity statement
identifies the corresponding angles and sides. Since
we know that , we can take the
corresponding angles of this statement and set them
congruent to each other. Then, since the
corresponding sides of similar triangles are
proportional to each other, we can write a proportion
thatrelatesthecorrespondingsidestoeachother.
47.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding a
this statement and set them congruent to each other.
the corresponding sides of similar triangles are propor
each other, we can write a proportion that relates the
correspondingsidestoeachother.
48.
SOLUTION:
The order of vertices in a similarity statement identifi
corresponding angles and sides. Since we know that
, we can take the corresponding
statement and set them congruent to each other. The
corresponding sides of similar polygons are proportio
other, we can write a proportion that relates the corr
sidestoeachother.
Solve each proportion.
49.
SOLUTION:
Cross multiply.
Solve for x.
50.
SOLUTION:
Cross multiply.
Solve for x.
51.
SOLUTION:
Cross multiply.
Solve for x.
52.
SOLUTION:
Cross multiply.
Solve for x.
53.
TANGRAMS
A tangram set consists of seven
pieces: a small square, two small congruent right
triangles, two large congruent right triangles, a
medium-sized right triangle, and a quadrilateral. How
can you determine the shape of the quadrilateral?
Explain.
SOLUTION:
Consider the properties of different quadrilaterals
when answering this question. The shape appears to
beaparallelogram,thereforeyoucantestthe
conditions of a parallelogram to see if they are true
forthisshape.
Sample answer: If one pair of opposite sides are
congruent and parallel, the quadrilateral is a
parallelogram.
Determine which postulate can be used to
prove that the triangles are congruent. If it is
not possible to prove congruence, write not
possible.
54.
SOLUTION:
We are given two pairs of congruent sides and a pair
of congruent angles. However, the congruent angles
are not the include angle between the two sides.
Therefore, it is a SSA relationship, not a SAS
relationship and it is not possible to prove these
trianglescongruent.
55.
SOLUTION:
We are given one pair of congruent angles and one
pair of congruent sides ( by Reflexive property).
However, it not possible to prove these triangles
congruent because we can't prove any other pair of
sidesoranglescongruent.
56.
SOLUTION:
Wearegiventhattwopairsofsidesarecongruent
and can prove the third pair of sides is, as well, by
using Reflexive property. Therefore, these triangles
can be proven congruent with SSS.
Write a two-column proof.
57.
Given:
Prove:
SOLUTION:
There are many angles in this diagram, so it is easy
to get confused by which ones to use. Notice how
the given statement guides you to using and .
Because they have different transversals, they are
not related to the same set of parallel lines. However,
they are both related to . If you can think about
how to get supplementary to , then you can
prove that
.
Given:
Prove:
Proof:
Statements (Reasons)
1.
(Given)
2.
(Consecutive Interior Angle
Theorem)
3.
(Definitionofsupplementary
angles)
4. (Definition of congruent angles)
5.
(Substitution)
6.
(Definition of supplementary)
7.
(Ifcons.int.
s are suppl., then lines are
||.)
eSolutionsManual-PoweredbyCogneroPage23
9-3 Similar Triangles
