Math 181 Calculus II
Worksheet Booklet
Department of Mathematics, Statistics, and Computer Science
University of Illinois at Chicago
THIS PAGE HAS BEEN INTENTIONALLY LEFT BLANK

Math 181 Worksheets
About this Booklet
This booklet contains worksheets for the Math 181 Calculus II course at the University
of Illinois at Chicago.
There are 28 worksheets, each covering a certain topic of the course curriculum. In a
15-week semester, completing 2 worksheets a week, there should be enough time to complete
all the worksheets.
Each worksheet, except the reviews, begins with a list of keywords. These are sorted in
the index at the end of the booklet, to make studying and topic-finding easier. The elec-
tronic version of this booklet has a hyperlinked index. The calculator icon in the margin
indicates that a certain question can be done with a calculator. A double exclamation point
!! in the margin indicates that a certain question is noticeably more difficult than the others.
To both students and instructors using this booklet - if you find any mistakes, or would
Acknowledgments
This booklet was first organized by Martina Bode, Director of Calculus at UIC, at the
end of the Spring 2016 semester. Robert Kozma, J¯anis Lazovskis, and John Lesieutre helped
put everything together for the first edition. The updates for the second and third editions
were put together by Matthew Fitzpatrick, Robert Kozma, and J¯anis Lazovskis.
Some questions, in modified form, are taken from Calculus: Early Transcendentals by
Briggs, Cochran, and Gillett, the textbook for this course.
Please attribute any use of the work in this booklet to the authors.
First printing: August 2018
This version typeset in L
A
T
E
X July 19, 2018.
i
Contents
Weekly Worksheets 1
1 Review 1: Definite integrals ..................................................................................... 1
2 Review 2: Fundamental theorem of calculus............................................................ 4
3 Working with integrals ............................................................................................. 7
4 Substitution.............................................................................................................. 10
5 Regions between curves and volumes ....................................................................... 13
6 Volumes by slicing.................................................................................................... 16
7 Length of curves and work ....................................................................................... 19
8 Integration by parts ................................................................................................. 23
9 More integration by parts and trigonometric integrals ............................................ 26
10 Partial fractions and improper integrals................................................................... 29
11 Introduction to sequences......................................................................................... 33
12 Introduction to series ............................................................................................... 36
13 The divergence, p-series, and ratio tests................................................................... 39
14 The comparison test................................................................................................. 42
15 The alternating series test and approximating functions with polynomials ............. 45
16 Power series.............................................................................................................. 49
17 Numerical integration............................................................................................... 53
18 Taylor series ............................................................................................................. 56
19 Parametric equations................................................................................................ 59
Math 181 Worksheets
20 Polar coordinates...................................................................................................... 62
21 Linear systems.......................................................................................................... 66
22 Matrices.................................................................................................................... 69
23 More matrices........................................................................................................... 72
24 Linear Maps ............................................................................................................. 76
Review Worksheets 80
1 Review for first midterm .......................................................................................... 80
2 Review for second midterm ...................................................................................... 86
3 Review for final exam (part one) ............................................................................. 91
4 Review for final exam (part two) ............................................................................. 96
Index 101
iii
THIS PAGE HAS BEEN INTENTIONALLY LEFT BLANK
Math 181 Worksheets
W1
1 Review 1: Definite integrals
Keywords: integration, definite integral, Riemann sum, area under curve
1. Illustrate and evaluate the following Riemann sums for f (x) = 1 + x
2
on the interval
[−1, 3] with n equally spaced subintervals by first calculating ∆x and the grid points
x
0
, x
1
, . . . , x
n
.
(a)
A left Riemann
sum with n = 4.
f(x)
(b)
A right Riemann
sum with n = 4.
f(x)
(c)
A midpoint Riemann
sum with n = 2.
f(x)
2. (a) For each subinterval in the left and right Riemann sums above, determine if the
corresponding Riemann rectangle is an underestimate or overestimate of the area
under the curve.
(b) In general, when is a left/right Riemann sum an overestimate/underestimate?
1

Math 181 Worksheets
W1
3. Write the definition of a definite integral
Z
b
a
f(x) dx as a limit of Riemann sums.
4. Set up a definite integral which represents the area under the curve f(x) = 1 + x
2
on
the interval [−1, 3].
5.!! Express the limit lim
n→∞
"
n
X
k=1
r
1 +
2k
n
· ln
1 +
2k
n
·
2
n
#
as a definite integral.
2

Math 181 Worksheets
W1
6. Suppose
Z
4
1
f(x) dx = 8 and
Z
6
1
f(x) dx = 5. Evaluate the following integrals.
(a)
Z
1
4
−3f(x) dx
(b)
Z
4
4
5f(x) dx
(c)
Z
6
4
f(x) dx
(d)
Z
4
6
2f(x) dx
7. Evaluate the following definite integral. Use the area interpretation of the integral.
Z
3
−3
√
9 − x
2
dx
3
Math 181 Worksheets
W2
2 Review 2: Fundamental theorem of calculus
Keywords: integration, definite integral, indefinite integral, Fundamental Theorem of Calcu-
lus, antiderivative
1. Consider the expressions
Z
b
a
f(t) dt and
Z
f(t) dt.
(a) What does each mean?
(b) How are the expressions different? Give as much detail as possible.
2. State the Fundamental Theorem of Calculus. (What is a “theorem?”)
3. Do you find it harder to take an integral or a derivative? Why? Use examples to show
what you mean.
4. Compute f
0
(x), where f is defined as the function
f(x) =
Z
x
4
1
2t ln(t
2
+ 5) dt.
Explain which theorems, and which differentiation techniques you are using. Hint: Let
g(x) =
Z
x
1
2t ln(t
2
+ 5) dt and h(x) = x
4
. Then you will have f (x) = g(h(x)).
4
Math 181 Worksheets
W2
5. The graph of f(x) is displayed below. Define g(x) =
Z
x
0
f(t)dt.
-2 2 4 6 8 10 12 14 16 18 20
-10
-5
5
10
15
20
x
y
f(x)
(a) On what intervals is g increasing?
(b) Find the local extrema of g. Indicate if each is a local minimum or local maximum.
(c) On what intervals is g concave upward? Hint: g
00
> 0 implies g
0
= f is increasing.
(d) Sketch a possible graph of g.
5

Math 181 Worksheets
W2
6. Evaluate the integrals below.
(a)
Z
4
1
3
√
x −
2
x
dx
(b)
Z
π
0
−2 cos(x) dx
(c)
Z
0
1
e
x
dx
(d)
Z
2
−3
(3x
2
+ 4x) dx
(e)!!
Z
1
−1
4|x
3
+ sin(πx)|dx
6

Math 181 Worksheets
W3
3 Working with integrals
Keywords: odd functions, even functions, symmetry, integration, average value, symmetric
functions
1. Use symmetry arguments to evaluate the following integrals.
(a)
Z
1
−1
3|x
3
|dx
(b)
Z
π
−π
sin
3
(x) + cos(x) dx
(c)
Z
2
−2
(3x
7
+ 2x
5
− 5x
4
+ x
3
− x) dx
(d)
Z
5
−5
2x
3
− x
x
4
+ 1
dx
7
Math 181 Worksheets
W3
2. Find the average value of the following functions on the given interval.
(a) f(x) = x
4
on [0, 5].
(b) f(x) =
2
x
on [1, e].
(c) f(x) =
1
x
2
+ 1
on [−
1
2
, 1].
(d) f(x) = sin(4x) on [−
π
2
,
3π
4
].
8

Math 181 Worksheets
W3
3. Find all points at which the given function equals its average value on the given interval.
(a) f(x) = 4 − x on [0, 2].
(b) f(x) =
1
x
on [1, 5].
(c) f(x) = 2 − |x| on [−2, 2].
4. The elevation of a hiking trail is given by f (x) = 2x
3
− 3x
2
+ 10, where x measures
the horizontal distance in miles from the trail head at x = 0. What is the average
elevation of the trail for the first three miles?
9

Math 181 Worksheets
W4
4 Substitution
Keywords: integration, substitution, trigonometric functions, exponential functions
1. Use the given substitutions to find the following indefinite integrals. Check your work
by differentiating.
(a)
Z
(6x + 1)
3
√
3x
2
+ x dx with u = 3x
2
+ x.
(b)
Z
sin
3
(x) cos(x) dx with u = sin(x).
(c)
Z
tan
2
(θ) sec
2
(θ) dθ with u = tan(θ).
10
Math 181 Worksheets
W4
2. Use integration by substitution to evaluate the following integrals.
(a)
Z
xe
x
2
dx
(b)
Z
x
√
x
2
+ 4 dx
(c)
Z
f
0
(x)
f(x)
dx
(d)!!
Z
x
√
4 − x dx
11

Math 181 Worksheets
W4
3. Consider the integral
Z
e
4
e
dx
x
√
ln x
.
(a) What is a good choice of u when doing substitution?
(b) What are the new limits of integration in terms of u?
(c) Evaluate the integral.
4. Evaluate the following integrals. Don’t forget that when the variable of integration is
changed from x to u, the limits of integration must also be expressed in terms of u.
(a)
Z
e
2
e
ln
2
(x)
x
dx
(b)
Z
1
0
x
2
√
2x
3
+ 1 dx
(c)
Z
π/16
0
cos
2
(8θ) sin(8θ) dθ
5. Write down and solve a definite integral which can be nicely solved using substitu-
tion. How elegant can you make it? Can you come up with one that requires three
substitutions to solve?
12
Math 181 Worksheets
W5
5 Regions between curves and volumes
Keywords: area, region between curves, area of compound regions, volume, slicing method
1. Sketch the given curves and indicate the region that is bounded by both. Then set up
and evaluate an integral representing the area of the region.
(a) y = x and y = x
2
− 2.
for −
π
4
≤ x ≤
π
4
.
-2 -1 1 2
-2
-1
1
2
x
y
(b) x = sin(y) and x = cos(y)
for
π
4
≤ y ≤
5π
4
.
-1 1
1
2
−
1
2
π
4
π
2
3π
4
π
5π
4
x
y
2. Consider region bounded by the curves y = 2
x
, y = 3 − x, and the y-axis.
(a) Draw the curves and shade in this region.
(b) Find the area of this shaded region by integrating with respect to x.
(c) Find the area of the region by integrating with respect to y. You may assume
that x ln(x) − x is an antiderivative of ln(x).
-2 -1 1 2
1
2
3
x
y
13

Math 181 Worksheets
W5
3. When setting up the integral for the area of a region bounded by curves, how do you
determine if you should integrate with respect to x or with respect to y? In what cases
would you / would you not draw a picture? Why?
4. (a) Give a pair of functions that intersect at least twice, so that the area of the region
they both bound is most easily found by integrating with respect to x. Draw their
graphs below.
(b) Give a different pair of functions (don’t just change the variables from part (a))
that intersect at least twice, so that the area of the region they both bound is
most easily found by integrating with respect to y. Draw their graphs below.
14
Math 181 Worksheets
W5
5. Let R be the region bounded by the circle of radius 1 centered at (2, 1).
(a) Draw the circle and shade in the region R below.
-3 -2 -1 1 2 3
1
2
x
y
(b) Sketch the solid S obtained by revolving R about the y-axis.
(c) Set up the integral representing the volume of the solid S.
15
Math 181 Worksheets
W6
6 Volumes by slicing
Keywords: area, region between curves, volume, slicing method, solid of revolution
1. Let R be the region bounded by the curves y =
√
25 − x
2
and y = 0.
(a) Draw the curves and shade in the region R below.
-5 -4 -3 -2 -1 1 2 3 4 5
1
2
3
4
5
x
y
(b) Suppose R is revolved around the x-axis to create a solid shape.
i. What does the cross-section of this shape look like at x = 3?
ii. Set up the integral for the volume of this solid.
(c) Verify that your answer agrees with the volume formula of a sphere.
16
Math 181 Worksheets
W6
2. Let R be the region bounded by the parabolas x = 1 − y
2
and x = y
2
− 1.
(a) Draw the parabolas and shade in the region R below.
(b) Set up the integral representing the volume of the solid obtained by rotating the
region R about the line x = −2. It may help to draw the shape of a cross-section
of the solid.
-2 -1 1 2
-2
-1
1
2
x
y
3. Let S be the solid whose base is bounded by the curves y = x
2
and y = 2 − x
2
, and
whose cross-sections perpendicular to the base are squares.
(a) Draw the curves and shade in the base below.
(b) Make a sketch of what you think the solid S looks like.
(c) Set up the integral representing the volume of S.
-1 1
1
2
x
y
17
Math 181 Worksheets
W6
4. Let R be the region bounded by y = 1/x, y = 0, x = e and x = e
2
.
(a) Make a sketch of the region.
1 2 3 4 5 6 7 8 9 10
1
1
2
3
2
x
y
(b) Set up the integral for the volume of the solid obtained by rotating the region R
around y = −1.
(c) Set up the integral for the volume of the solid obtained by rotating the region R
around y = 1.
18
Math 181 Worksheets
W7
7 Length of curves and work
Keywords: arc length, length of curves, physical applications, work, pumps, springs
1. (a) Find the arc length of the curve y = −
3
4
x + 1 where x is in [−4, 4].
(b) Sketch the curve below.
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
-3
-2
-1
1
2
3
4
5
(c) Check whether your answer from (a) is correct by using the Pythagorean theorem
on (b).
19

Math 181 Worksheets
W7
2. For each of the following curves, set up an integral representing its arc length.
(a) y =
2
3
(x − 1)
2
on the interval [1, 4].
(b) y = x
5/4
on the interval [0, 1].
(c) y = 1/x on the interval (0, 4]. Knowing the graph of 1/x, what is the arc length?
3. Compute the arc length of the curve y =
x
3
3
+
1
4x
on the interval [1, 3].
4. The hyperbolic cosine function cosh(x) is defined as cosh(x) =
1
2
(e
x
+ e
−x
). Find the
arc length of cosh(x) on the interval [−ln(2), ln(2)].
20
Math 181 Worksheets
W7
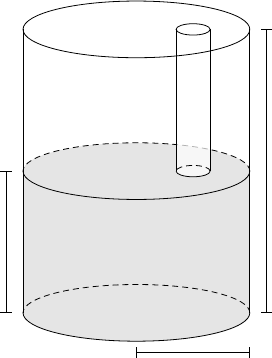
5. A tank shaped like a cylinder, with a height of 10 meters and a radius of 1 meter, is
half filled with water. A hose is dropped in from the top to the surface of the water,
where it floats, as in the diagram below.
5m
1m
10m
(a) Set up and evaluate an integral representing the work needed to pump the water
out of the tank through the hose. The density of water is 1000 kg/m
3
, and you
may assume that the acceleration due to gravity is 10 m/s
2
.
(b) Repeat part (a) in the situation that only one fifth of the tank has been filled.
(c) Repeat part (a) in the situation that the tank is a rectangular prism, whose base
is a rectangle of width 2 m and length 3 m (the height is still 10 m). Sketch the
diagram first.
21
Math 181 Worksheets
W7
6. A spring has a natural length of 0.2 m. A force of 10 N is required to stretch the spring
to a length of 0.3 m.
(a) If we apply a force of 27 N to stretch the spring, what is the spring’s length?
Hint: Recall that Hooke’s law states the force required to keep a spring stretched
or compressed x units from its natural length is F(x) = kx, where k is the spring’s
constant.
(b) How much work is done to stretch the spring from 0.2 m to 0.3 m?
7.!! Four Brothers, the new fast food chain, was making a delivery of their house root beer.
The root beer initially filled a container that is in the shape of an inverted cone with
a height of 10 m and a top radius of 2 m. The crew of Four Brothers is using a Super
Suction machine to pump the root beer to the top of the container. The motor on the
pump stopped working when the height of the remaining root beer in the container
was 3 m. Using the facts that the density of the house root beer is 160 kg/m
3
and the
acceleration due to gravity on earth is approximately 10 m/s
2
, set up an integral that
describes the amount of work that was done by the pump.
22
Math 181 Worksheets
W8
8 Integration by parts
Keywords: integration by parts, definite integral, indefinite integral
1. Use integration by parts twice to integrate
Z
x
2
sin(2x) dx.
2. For each of the following integrals, how many iterations of integration by parts is
required to evaluate it? Do not evaluate the integrals, but explain your reasoning.
(a)
Z
x
5
sin(x) dx
(b)
Z
(y
5
+ 3y
3
− y
2
) cos(3y) dy
23

Math 181 Worksheets
W8
3. Evaluate the integral
Z
x
√
x − 2
dx
(a) using substitution.
(b) using integration by parts.
(c) Reconcile the results of (a) and (b).
24
Math 181 Worksheets
W8
4. Use integration by parts to evaluate the following integrals.
(a)
Z
(x + 3) sin(2x) dx
(b)
Z
(2x − 1)e
x
dx
(c)
Z
e
1
ln(2x) dx
5. Use integration by parts twice to integrate
Z
e
3x
cos(3x) dx.
25

Math 181 Worksheets
W9
9 More integration by parts and trigonometric inte-
grals
Keywords: integration by parts, trigonometric integration, trigonometric functions
1. Use integration by parts to evaluate the following integrals.
(a)
Z
sin(2z) cos(3z) dz
(b)
Z
1
2
0
arccos(θ) dθ
26
Math 181 Worksheets
W9
2. (a) State the half angle identities used to integrate sin
2
(x) and cos
2
(x).
(b) State the Pythagorean identities.
(c) Use the above identities to evaluate the following integrals.
i.
Z
4 cos
4
(x) dx
ii.
Z
sin
2
(φ) cos
2
(φ) dφ
iii.
Z
tan
2
(θ) dθ
27
Math 181 Worksheets
W9
3. Use trigonometric identities and substitution to evaluate the following integrals.
(a)
Z
sin
3
(x) cos
2
(x) dx
(b)
Z
6 sin
2
(y) cos
5
(y) dy
4. Evaluate
Z
sec
4
(θ) dθ. Hint: Use the Pythagorean identity sec
2
(x) = 1 + tan
2
(x).
28

Math 181 Worksheets
W10
10 Partial fractions and improper integrals
Keywords: partial fractions, factoring, long division, polynomials, improper integral, infinite
limit of integration, infinite intervals, unbounded integrands
1. Write out the form of the partial fraction expansion for the following functions. Do
not determine the numerical values of the coefficients.
(a)
x
2
− 2x + 3
x
3
− x
2
− 6x
=
(b)
x + 1
x
3
+ 2x
2
=
(c)
5
(x
2
− 1)(x
2
+ 1)
=
2. Evaluate the following integrals. You will have to use partial fractions, factoring, and
polynomial division.
(a)
Z
1
(x − 3)(x + 1)
2
dx
(b)
Z
dx
x
2
− 7x + 10
29
Math 181 Worksheets
W10
3. Rewrite each the following improper integrals as a limit. If it converges, evaluate it.
The first one is done for you.
(a)
Z
∞
1
dx
x(x + 1)
= lim
b→∞
Z
b
1
dx
x(x + 1)
= lim
b→∞
Z
b
1
1
x
−
1
x + 1
dx = lim
b→∞
ln |x| − ln |x +
1|
b
1
= lim
b→∞
ln
x
x + 1
b
1
= lim
b→∞
ln
b
b + 1
− ln
1
2
= ln(1) + ln(2) = ln(2) since the
partial fraction decomposition of
dx
x(x + 1)
is
1
x
−
1
x + 1
.
(b)
Z
∞
2
dx
√
x
(c)
Z
3
2
dy
y − 3
(d)
Z
∞
1
ln(x)
x
3
dx
(e)
Z
0
−∞
x
2
e
x
3
dx
30
Math 181 Worksheets
W10
4. For which values of p does the integral
Z
∞
1
1
x
p
dx converge and for what values of
p does it diverge? Hint: The antiderivative of x
−p
takes one form when p 6= 1 and
another form when p = 1.
5. Using comparison, determine if the following integrals converge or diverge.
(a)
Z
∞
1
cos
2
(x)
x
2
dx
(b)
Z
∞
1
dx
ln(x)
31

Math 181 Worksheets
W10
6. Gabriel’s horn, also called Torricelli’s trumpet, is the surface of revolution of the func-
tion y = 1/x about the x-axis for x ≥ 1.
(a) Find the volume of Gabriel’s horn.
(b) The surface area of a surface of revolution defined by the function f, revolved
around the x-axis from x = a to x = b is given by the formula
Z
b
a
2πf(x)
p
1 + f
0
(x)
2
dx.
Find the surface area of Gabriel’s horn or show that it is infinite. Hint: Use
comparison.
(c) Reconcile the results of (a) and (b).
32

Math 181 Worksheets
W11
11 Introduction to sequences
Keywords: sequences, recursive sequences, limits of sequences, convergence, divergence
1. Find an explicit formula for the nth term of the following sequences. The first term
given in each sequence is for n = 1.
(a) 16, 25, 36, 49, . . .
(b)
1
2
,
2
3
,
3
4
, . . .
(c) 1,
−1
4
,
1
27
,
−1
256
, . . .
(d) −1, 1, −1, 1, −1, 1, . . .
(e) 0, 1, 0, 1, 0, . . .
(f) 1, 1, 2, 2, 3, 3, 4, . . .
2. Find the limit of each sequence as n goes to infinity or state that it does not exist.
(a) a
n
=
n
3
n
4
+ 1
(b) b
n
=
ln(n)
n
(c) c
n
=
ln(
1
n
)
n
(d) d
n
=
(−1)
n
√
n
(e)!! e
n
=
1 +
4
n
n
(f) f
n
=
sin(
nπ
8
)
√
n
33
Math 181 Worksheets
W11
3. Let a
n
be given by the recurrence relation
1
a
n+1
=
1
2
a
n
+
2
a
n
, a
0
= 1 .
(a) Calculate the first three terms of the sequence.
(b) Assuming the limit exists, calculate lim
n→∞
a
n
.
4.!! Let a
n
be the sequence given by a
n
=
1 −
1
2
1 −
1
3
. . .
1 −
1
n
.
(a) Calculate the first four terms of the sequence.
(b) Find the limit of the sequence as n goes to infinity.
1
This is perhaps the first algorithm used for approximating
√
S, known as the “Babylonian method”. It
is a quadratically convergent algorithm, which means that the number of correct digits of the approximation
roughly doubles with each iteration. It proceeds as follows: Start with an arbitrary positive start value x
0
(the closer to the root, the better). Let x
n+1
be the average of x
n
and S/x
n
. Repeat until the desired
accuracy is achieved.
34

Math 181 Worksheets
W11
5. Give an example of each of the following sequences. Use a different one for each!
(a) non-increasing sequence
(b) increasing sequence
(c) non-decreasing sequence
(d) decreasing sequence
(e) constant sequence
(f) monotonic sequence
(g) sequence that is bounded below
(h) sequence that is bounded above
(i) bounded sequence
(j) convergent sequence
6. Notice that 0.9 =
9
10
, 0.99 =
9
10
+
9
100
and so on.
(a) Use this pattern to define a sequence {a
n
} such that
∞
X
n=1
a
n
= 0.99999 . . . .
(b) Use this pattern to define a sequence {a
n
} such that
∞
X
n=1
a
n
= 0.1234123412 . . . .
35

Math 181 Worksheets
W12
12 Introduction to series
Keywords: series, convergence, divergence, partial sums, infinite series, geometric series,
telescoping series
1. Consider the sequence
4, −
4
5
,
4
25
, −
4
125
, . . .
(a) Find a formula for the general term a
n
of this sequence.
(b) Find lim
n→∞
a
n
.
(c) Does the series
∞
X
n=1
a
n
converge or diverge? If it converges, find its sum.
2. Determine whether the following telescoping series converge or diverge by finding a
formula for the k-th partial sum and evaluating its limit if the limit exists.
(a)
∞
X
n=2
1
n(n − 1)
(b)
∞
X
n=1
ln
n + 1
n
36

Math 181 Worksheets
W12
3. Determine whether the following geometric series converge or diverge. For each series
find the ratio r and its first term a. If the series converges, compute its sum.
(a)
∞
X
n=1
(−4)
n
9
n
(b)
∞
X
n=1
(−4)
2n
3
n
4. Evaluate the following sums (do not use brute force).
(a)
12
X
k=0
2
k
(b)
10
X
n=1
4
7
n
(c) What happens if we take these two sums up until infinity? Do they converge or
diverge?
37

Math 181 Worksheets
W12
5. Write the repeating decimal 0.456 first as a geometric series and then as a simplified
fraction.
6. Koch Snowflake Fractal The fractal called the Koch Snowflake is constructed as
follows: Let I
0
be an equilateral triangle with sides of length 1. The figure I
1
is obtained
by replacing the middle third of each side of I
0
with a new outward equilateral triangle
with sides of length 1/3. The process is repeated where I
n+1
is obtained by replacing
the middle third of each side of I
n
with a new equilateral triangle with sides of length
1/3
n+1
. The limiting figure as n → ∞ is called the Koch Snowflake.
(a) First draw the first three stages of the construction.
(b) Let L
n
be the perimeter of I
n
. Show that lim
n→∞
L
n
= ∞, i.e. the perimeter is
infinite.
(c) Let A
n
be the area of I
n
. Find lim
n→∞
A
n
. Show that it exists and is finite!
(d) Compare the Koch Snowflake with Gabriel’s horn.
38

Math 181 Worksheets
W13
13 The divergence, p-series, and ratio tests
Keywords: series, divergence test, p-test, ratio-test, harmonic series, geometric series
1. If lim
k→∞
a
k
= 1, what can you say about
∞
X
k=1
a
k
?
2. If the terms of a positive series decrease to zero, then does the series converges? Given
an example or counter example to support your argument.
3. For what values of p does the series
∞
X
k=10
1
k
p
converge or diverge?
4. Determine whether the following statements are true or false.
(a) The series
∞
X
n=1
a
n
diverges if lim
n→∞
a
n
= 5.
(b) If the sequence {a
n
} converges, then the series
∞
X
n=1
a
n
converges.
(c) The series
∞
X
n=1
1
n
converges.
(d) The sequence
1
n
∞
n=1
converges.
39
Math 181 Worksheets
W13
5. Use the Ratio test to determine if the following series converge.
(a)
∞
X
n=1
n
2
2
n
(b)
∞
X
n=1
3
2n
n!
(c)
∞
X
n=1
(2n)!
5
n
40

Math 181 Worksheets
W13
6. Determine whether the following series converge or diverge.
(a)
∞
X
k=1
5
k
(b)
∞
X
k=1
k
3
− 1
k
3
+ 1
(c)
∞
X
k=2
k
e
k
π
(d)
∞
X
k=1
π
e
k
(e)
∞
X
k=1
e
1/k
− e
1/(k+1)
(f)
∞
X
k=1
3
(k
2
)!
(g)
∞
X
k=1
5
√
k
(h)
∞
X
k=1
2
k+1
+ (−2)
k
5
k
41

Math 181 Worksheets
W14
14 The comparison test
Keywords: series, comparison test, limit comparison test
1. Suppose
X
a
n
and
X
b
n
are series with positive terms and
X
b
n
converges.
(a) If a
n
< b
n
for all n, what can you say about
X
a
n
? Why?
(b) If a
n
> b
n
for all n, can you say anything about
X
a
n
? Why?
(c) What could you say in cases (a) and (b) if the series had negative terms instead?
2. Determine if
∞
X
n=1
−1
n
3
− 7n
2
+ 17n + 20
converges or diverges.
42

Math 181 Worksheets
W14
3. Consider the series
∞
X
n=2
n + 1
n
2
.
(a) Use the direct comparison test to determine if it converges or diverges.
(b) Now use the limit comparison test and see if you arrive at the same conclusion.
4. Consider the series
∞
X
n=2
n + 1
n
3
.
(a) Use the limit comparison test to determine if it converges or diverge.
(b) Why can’t you use the direct comparison test here?
43

Math 181 Worksheets
W14
5. Determine if the following series converge or diverge.
(a)
∞
X
n=1
sin(1/n)
n
3
(b)
∞
X
k=1
7k
4
+ 3k
2
+ 1
11k
5
− 4k
3
+ 9k
2
− 1
(c)
∞
X
n=1
1
7
n
− 5
n
(d)
∞
X
k=1
1
√
k − 3k
44

Math 181 Worksheets
W15
15 The alternating series test and approximating func-
tions with polynomials
Keywords: series, alternating series test, absolute convergence, conditional convergence, ap-
plications, approximation, power series, Taylor polynomials, linear approximation, quadratic
approximation
1. Determine whether the following series converge or diverge.
(a)
∞
X
n=2
(−1)
n
√
n
(b)
∞
X
n=2
(−1)
n
√
n
(c) Does the series
∞
X
n=2
(−1)
n
√
n
converge absolutely, converge conditionally, or diverge?
45

Math 181 Worksheets
W15
2. Determine whether the given series converges conditionally, converges absolutely, or
diverges. Justify your response by specifying which convergence tests you use and
verifying that the conditions of each used test are satisfied.
(a)
∞
X
n=0
(−1)
n
2
n
(b)
∞
X
n=1
(−2)
n
n!
46
Math 181 Worksheets
W15
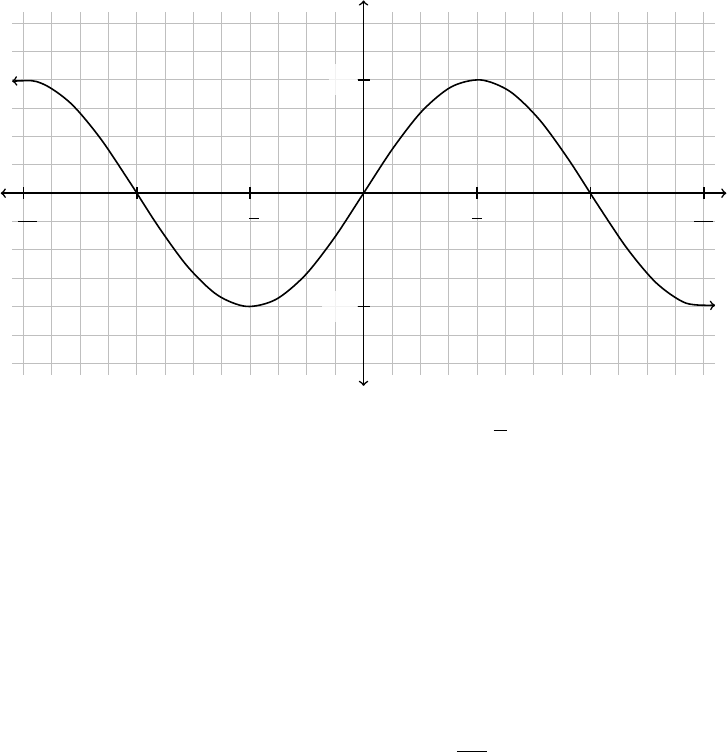
3. (a) Find the n-th order Taylor polynomial of the function f(x) = sin(x) centered at
a = 0 for n = 1, 2, and 3.
(b) Graph the above Taylor polynomials in the coordinate system below.
x
-1
1
-
3π
2
-π
-
π
2
π
2
π
3π
2
4. (a) Find the 3rd-degree Taylor polynomial of f(x) =
√
x centered at a = 1.
(b) Use your result from part (a) to approximate
√
0.9. You do not need to simplify
your answer.
47

Math 181 Worksheets
W15
5. Match the functions with their second degree Taylor polynomials centered at zero.
Give reasons for your choices!
a(x) =
√
1 + 2x p
2
(x) = 1 + 2x + 2x
2
b(x) =
1
√
1 + 2x
q
2
(x) = 1 − 6x + 24x
2
c(x) = e
2x
r
2
(x) = 1 + x −
x
2
2
d(x) =
1
1 + 2x
s
2
(x) = 1 − 2x + 4x
2
e(x) =
1
(1 + 2x)
3
t
2
(x) = 1 − x +
3
2
x
2
f(x) = e
−2x
u
2
(x) = 1 − 2x + 2x
2
6. (a) Find the 1st, 2nd, and 3rd degree Taylor polynomials of f(x) = x
2
centered at
a = 0.
(b) Find the 2nd degree Taylor Polynomial of f(x) = x
2
centered at a = 1.
(c) Compare your results from (a) and (b). What can you conclude?
48

Math 181 Worksheets
W16
16 Power series
Keywords: power series, radius of convergence, interval of convergence, combining power
series, differentiating power series, integrating power series
1. Determine the radius of convergence of the following power series. Then test the
endpoints to determine the interval of convergence.
(a)
∞
X
k=1
(x − 1)
k
k
Check endpoints:
(b)
∞
X
k=1
(−1)
k+1
(x − 1)
k
k3
k
Check endpoints:
49

Math 181 Worksheets
W16
(c)
∞
X
n=1
(x − 3)
n
2
n
√
n
Check endpoints:
2.!! Find the radius and interval of convergence of
∞
X
n=1
x
n
n
n
.
50

Math 181 Worksheets
W16
3. Use the geometric series
1
1 − x
=
∞
X
k=0
x
k
for |x| < 1, to find a power series representation
for the following functions.
(a) f(x) =
1
1 + x
(b) g(x) =
1
1 − x
2
(c) h(x) =
x
3
1 + x
(d) k(x) =
Z
x
3
1 + x
dx
(e) What are the radii of convergence of the power series above?
51

Math 181 Worksheets
W16
4.!! A tortoise and a hare wanted to determine which was the better animal so the tortoise
proposed a 100 m race. The hare thought the tortoise was foolish for wanting to race
and told the tortoise that he should just forfeit. The tortoise said, “if you are so
confident in your victory, you should give me a head start.” The hare replied, “you can
have a 20 m head start. It won’t matter since I’m much faster than you.” The tortoise
then said, “by giving me a head start you have lost the race.” The confused hare asked,
“how could that be? I’m significantly faster than you.” The tortoise explained, “no
matter how fast you are, it will take you some amount of time to reach the 20 m mark
and in that time I would have moved forward some distance. It will take you some
more time to go that distance in which I would have moved forward some more. In the
time it takes you to reach where I am then, I will have moved closer to the finish. We
can repeat this over and over. Every time you reach the position I was just at, I will
have moved some distance forward and will still be ahead. You will never be able to
pass me even if we do this an infinite amount of times since each time I will be some
distance ahead of you.” The hare, believing he would be defeated, decided to forfeit
giving the hare the victory. Explain to the hare, using sequences and series, why even
though what the tortoise said was true, the hare would have still won the race.
5. Let f(x) =
∞
X
k=0
x
2k
2
k
k!
.
(a) Show that f(x) has infinite radius of convergence.
(b) Show that f
0
(x) = xf(x).
52
Math 181 Worksheets
W17
17 Numerical integration
Keywords: numerical integration, midpoint rule, trapezoid rule, Simpson’s rule
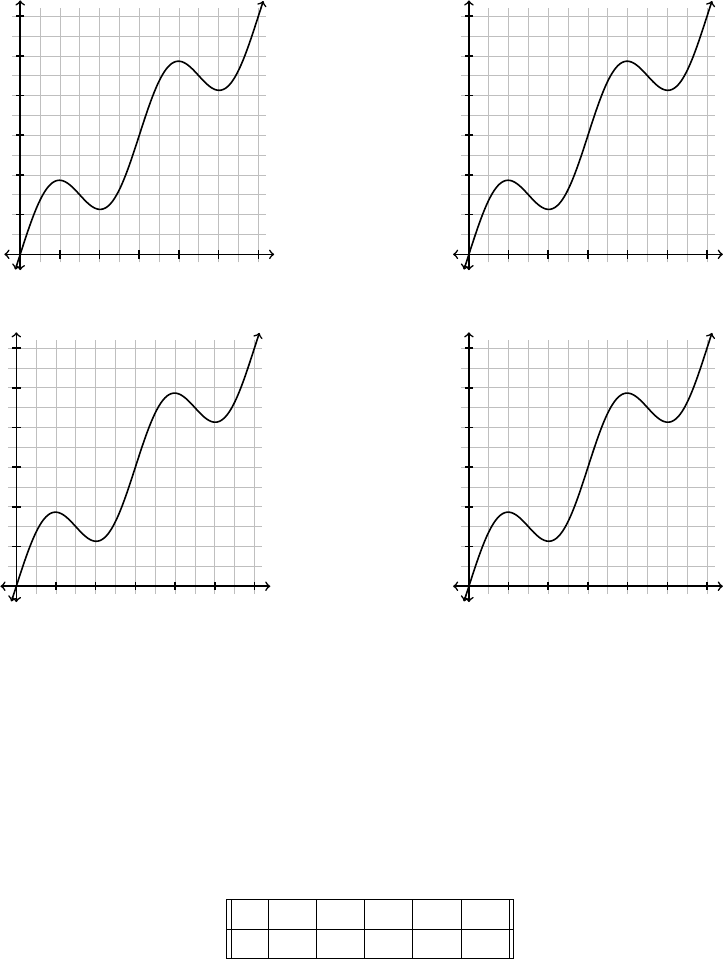
1. Complete the figures by graphing the missing approximations of the indicated numer-
ical integration techniques using n = 6 subintervals.
1 2 3 4 5 6
1
2
3
4
5
6
x
(a) left Riemann sum
f(x)
1 2 3 4 5 6
1
2
3
4
5
6
x
(b) right Riemann sum
f(x)
1 2 3 4 5 6
1
2
3
4
5
6
x
(c) midpoint Riemann sum
f(x)
1 2 3 4 5 6
1
2
3
4
5
6
x
(d) trapezoid rule
f(x)
2. In the previous problem, visually which integration technique do you think gives the
best approximation to f(x) from x = 0 to x = 6?
3. A submarine is traveling under the polar ice cap directly towards the North Pole. The
velocity v (in miles per hour) of the submarine is recorded below. Use Simpson’s Rule
to estimate the total distance the submarine traveled during the 8 hour period.
t 0 2 4 6 8
v 10 15 12 10 16
53
Math 181 Worksheets
W17
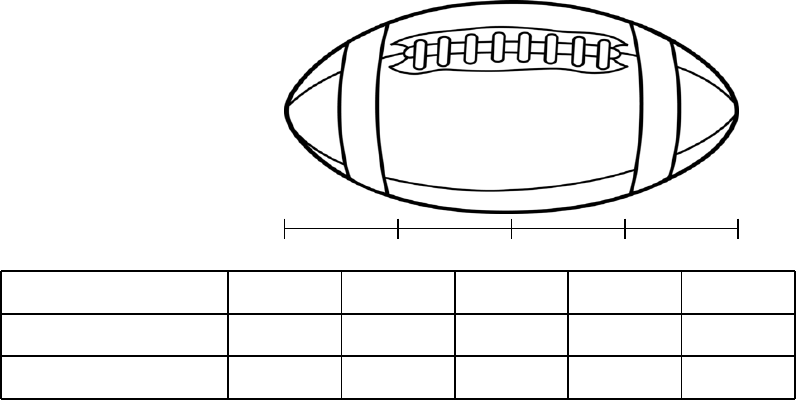
4. Suppose you’re asked to estimate the volume of a football. You measure and find that
a football is 28 cm long. You use a piece of string and measure the circumference at
its widest point to be 53 cm. The circumference 7 cm from the end is 45 cm.
(a) Use your measurements to complete the table which will assist you in estimating
the volume of the football.
0 cm 7 cm 14 cm 21 cm 28 cm
circumference
radius
cross-sectional area
(b) Use Simpson’s rule to make your estimate.
(c) Use the trapezoidal rule to make your estimate.
54
Math 181 Worksheets
W17
5. Using the trapezoid sum, calculate the area underneath the curve y = x
2
from 0 to 1,
when it is split up into n intervals, then take the limit as n → ∞.
6. Find the midpoint rule approximation for
Z
5
1
x
2
dx using n subintervals.
(a) n = 4
1 2 3 4 5 6
4
8
12
16
20
24
28
32
36
(b) n = 8
1 2 3 4 5 6
4
8
12
16
20
24
28
32
36
(c)!! Are these midpoint approximations over estimates or under estimates? Why?
Calculate the error of each estimate.
55

Math 181 Worksheets
W18
18 Taylor series
Keywords: Taylor series, series expansion, series approximation, Maclaurin series
1. Let f(x) = cos(πx).
(a) Evaluate f(1), f
0
(1), f
00
(1), f
000
(1), f
(4)
(1) and f
(5)
(1).
(b) Find the Taylor series expansion at x = 1 of the function f(x).
2. (a) Use the Maclaurin series e
x
= 1 + x +
x
2
2!
+
x
3
3!
+
x
4
4!
+ ··· to find the Maclaurin
series of e
(x
3
)
.
(b) Use the first three non-zero terms of the series you found in the previous problem
to approximate the definite integral
Z
1
0
e
(x
3
)
dx.
56

Math 181 Worksheets
W18
3. Suppose f(x) =
∞
X
k=1
(−1)
k+1
x
k
k
2
= x −
x
2
4
+
x
3
9
−
x
4
16
+ ···
(a) Find the first three non-zero terms of the power series representing the function
xf(x
2
).
(b) Use your results in part (a) to approximate the indefinite integral
Z
xf(x
2
) dx.
4.!! Using the Taylor series for xe
x
centered at x = 0, show that
∞
X
n=0
n + 1
n!
= 2e.
57

Math 181 Worksheets
W18
5. Consider the series f(x) =
∞
X
k=0
(2x + 3)
k
k!
.
(a) Find the derivative f
0
(x) of the series and rewrite it in terms of f(x).
(b) Using part (a), give the nth derivative of f(x). Do not simply keep taking deriva-
tives of the series.
(c) What common function is f(x) equal to?
58
Math 181 Worksheets
W19
19 Parametric equations
Keywords: parametric equations, circles, arcs, ellipses, circular motion, slope
1. Eliminate the parameter t to obtain a single equation for the parametric curves in
terms of only x and y. Make a rough sketch of these curves, and indicate with arrows
the direction of motion.
(a) x = 6t − 2, y = 3t
-4 -3 -2 -1 1
-1
1
2
x
y
(b) x = sin(t) + 2, y = cos(t)
-1 1 2 3 4
-1
1
x
y
59
Math 181 Worksheets
W19
2. A Ferris wheel has a radius 20 m and completes a revolution in the clockwise direction
at constant speed in 3 min. Assume that x and y measure the horizontal and vertical
positions of a seat on the Ferris wheel relative to the coordinate system whose origin
is at the low point of the wheel. Assume that the seat begins moving at the origin.
(a) Find the parametric equations that describe the position of the seat at time t.
(b) What is the position of the rider when t = 1 min?
3. Consider the parametric curve given by x = 4t
2
+ 1 and y = 2t.
(a) Determine dy/dx in terms of t and evaluate it at t = −1.
(b) Make a sketch of the curve showing the tangent line at the point corresponding
to t = −1.
1 2 3 4 5 6 7 8 9 10
-3
-2
-1
1
2
3
x
y
60
Math 181 Worksheets
W19
4. Match each of the equations (a)-(d) with one of graphs (i)-(iv). Explain your reasoning.
(a) x = t
2
− 2, y = t
3
− t
(b) x = cos(t + sin(50t)), y = sin(t + cos(50t))
(c) x = t + cos(3t), y = t − sin(3t)
(d) x = 2 cos(t) + cos(10t), y = 2 sin t + sin(10t)
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(i)
-1 1-1.5 -0.5 0.5 1.5
-1
1
-1.5
-0.5
0.5
1.5
x
y
(ii)
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(iii)
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(iv)
61
Math 181 Worksheets
W20
20 Polar coordinates
Keywords: polar coordinates, Cartesian coordinates, polar coordinates, polar curves, Cartesian-
to-polar method
1. For each of the following conversions plot the point and convert.
Convert from Cartesian to Polar coordi-
nates:
-2 -1 1 2
1
2
3
4
x
y
(a) (0, 2)
-4 -3 -2 -1
-2
-1
1
2
x
y
(b) (−3, 0)
-2 -1 1 2
-2
-1
1
2
x
y
(c) (−
√
2,
√
2)
Convert from Polar to Cartesian coordi-
nates:
-2 -1 1 2
-2
-1
1
2
x
y
(d) (−1,
π
2
)
-2 -1 1 2
-2
-1
1
2
x
y
(e) (2,
2π
3
)
-2 -1 1 2
-2
-1
1
2
x
y
(f) (−2,
2π
3
)
62
Math 181 Worksheets
W20
2. Consider the polar curve given by the equation r = 2 cos(3θ) with 0 ≤ θ ≤ π.
(a) Fill in the values of r in
the table below.
θ r
0
π/6
π/3
π/2
2π/3
5π/6
π
(b) Sketch the curve in the θr-plane.
π
6
π
3
π
2
2π
3
5π
6
π
-2
-1
1
2
θ
r
(c) Sketch the curve in the xy-plane. Label the points from the table.
-2 -1 1 2
-2
-1
1
2
x
y
63
Math 181 Worksheets
W20
3. Consider the polar functions r
1
(θ) =
θ
π
and r
2
(θ) = −
θ
π
defined on 0 ≤ θ ≤ 4π.
(a) Fill in the table below.
θ r
1
(θ) r
2
(θ)
0
π/2
π
3π/2
2π
5π/2
3π
(b) Sketch r
1
(θ) in the plane.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(c) Sketch r
2
(θ) in the plane.
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(d) How do the two graphs differ? What
does multiplying a polar function by −1
do to it graphically in the xy-plane?
64
Math 181 Worksheets
W20
4. Match each of the equations (a)-(c) with one of the Cartesian graphs (i)-(iii) and one
of the Polar graphs (I)-(III). Explain your reasoning.
(a) r =
1
4
− cos(4θ)
(b) r = sin(1 + 3 cos(θ))
(c) r = 1 − 2 sin(3θ)
π
2
π
3π
2
2π
-0.5
0.5
1
x
y
(i)
π
2
π
3π
2
2π
-0.5
0.5
-1
1
x
y
(ii)
π
2
π
3π
2
2π
-1
1
2
3
x
y
(iii)
-1 1
-1
1
x
y
(I)
-1 1
-1
1
x
y
(II)
-3 -2 -1 1 2 3
-3
-2
-1
1
2
3
x
y
(III)
65
Math 181 Worksheets
W21
21 Linear systems
Keywords: linear systems, system of equations, matrix, matrix multiplication, linear systems,
augmented matrix
1. We’re going to look at the system of linear equations
3x − 2y = 1
2x − y = 1.
(a) Solve this system of equations using algebra.
(b) Draw the graphs of the equations for the two lines. Where do they intersect?
-4 -3 -2 -1 1 2 3 4 5 6
-3
-2
-1
1
2
3
4
5
x
y
66
Math 181 Worksheets
W21
2. The system of equations
x + 2y = 6
2x + 4y = 13
has no solutions. What happens when you try to solve the system using:
(a) algebraic manipulations?
(b) a graph of the lines?
-5 -4 -3 -2 -1 1 2 3 4 5
-1
1
2
3
4
5
6
7
x
y
67
Math 181 Worksheets
W21
3. For what values of a does the system of equations 2x − y = a, 4x − 2y = 3 have a
solution. How do the graphs of the lines change when you change the value of a?
4. For what values of a does the system of equations 2x − y = a, ax + y = 1 have a
solution? How do the graphs of the lines change when you change the value of a?
5. A movie made $15 million online from a mix of sales and rentals. A sale costs $16, and
a rental costs $5. Given that there were a total of 2 million transactions, how many
were rentals and how many were sales?
6. You are trying to mix up 2 cups of a cinnamon-sugar topping consisting of 4/5 sugar
and 1/5 cinnamon. You already have a large bag that is half sugar and half cinnamon,
and a large bag full of pure sugar. How much should you take from each bag to get
the correct mix?
68

Math 181 Worksheets
W22
22 Matrices
Keywords: inverse matrix, determinants, linear systems
1. Give an example of a:
(a) 2 × 3 matrix with real entries.
A =
π 4 −e
3
2
0 1
(b) 3 × 1 matrix with real entries.
B =
(c) 2 × 3 matrix with integer entries.
C =
(d) 3 × 3 matrix with integer entries.
D =
2. Consider the matrices
A =
1 2
3 2
, B =
−1 3
−2 1
.
(a) Compute 3A and B −3A. Can you find a matrix C that satisfies 3A−B + C = 0?
(b) Compute AB and BA.
3. Let A be the matrix
A =
2 1
1 1
.
Compute A
2
.
69
Math 181 Worksheets
W22
4. Let
A =
1 2
2 4
, B =
2 4
1 4
, C =
4 6
0 3
.
Check that AB = AC, even though B 6= C.
5. The previous worksheet considered the system of equations
3x − 2y = 1
2x − y = 1
(a) Write down the augmented matrix corresponding to the system of equations, and
use elimination to solve for x.
(b) For each step, write down the system of linear equations corresponding to your
matrix.
(c) Does this match your answer from last time?
70

Math 181 Worksheets
W22
6. Consider the following augmented matrix:
1 −3 4
−2 6 −8
(a) What is the corresponding system of linear equations?
(b) Solve this system using elimination.
(c) What happens if the third column is replaced by
4
8
?
71
Math 181 Worksheets
W23
23 More matrices
Keywords: inverse matrix, determinants, linear systems
1. Find the determinants of the following matrices:
(a) A =
−1 1
−1 3
(b) B =
2 3
1 1
(c) C =
2 a
0 3
(d) D =
cos θ sin θ
sin θ −cos θ
72
Math 181 Worksheets
W23
2. Consider the matrix
C =
4 9
1 2
.
(a) Compute C
−1
.
(b) Double-check your answer by multiplying out CC
−1
and C
−1
C.
(c) Use the first part to solve the linear system Cx =
1
1
.
73
Math 181 Worksheets
W23
3. In the previous worksheet, we looked at the system of equations
3x − 2y = 1
2x − y = 1.
(a) How can you write this system in matrix form Ax = b?
(b) What is the inverse of the matrix A? Double-check your answer by multiplying
out AA
−1
and A
−1
A. What answer should you get?
(c) Solve the linear system by multiplying both sides on the left by A
−1
. Does this
match your previous answer?
74
Math 181 Worksheets
W23
4. Last week, we saw that the system
x + 2y = 6
2x + 4y = 13
does not have any solutions.
(a) Write this system of equations in matrix form.
(b) What happens when you try to solve by multiplying by A
−1
?
75
Math 181 Worksheets
W24
24 Linear Maps
Keywords: vectors, eigenvectors, eigenvalues, linear maps, rotations, identity map
1. Let x =
1
1
and y =
−1
2
. Compute and graph the vectors 2x, 3y, and 2x + 3y.
-2 -1 1 2 3 4 5 6 7 8 9 10
-3
-2
-1
1
2
x
y
2. Consider the transformation T (x) =
0 0
0 1
x
y
.
(a) Plot u =
1
2
, v =
2
−4
, and their im-
ages under the transformation T . De-
scribe geometrically what T does to
each vector in the xy-plane.
(b) Repeat the previous exercise for the
transformations
S(x) =
1 0
0 1
x
y
and
R(x) =
0 1
1 0
x
y
.
-4 -3 -2 -1 1 2
-4
-3
-2
-1
1
2
x
y
76
Math 181 Worksheets
W24
3. Let A be the matrix
A =
1 2
3 4
(a) Compute Ax, where x is the vector
1
1
. What about 3x?
(b) Compute Ay, where y is the vector
−1
3
.
(c) What is the vector x − 2y? Check that A(x −2y) = Ax −2Ay.
(d) Find a vector x so that Ax =
4
10
.
77

Math 181 Worksheets
W24
4. Can you come up with a matrix A so that Ax is the vector x rotated by 60 degrees
counterclockwise? Check your answer by applying it to a vector of your choice.
5. Let A =
3 2
3 8
, x =
−4
2
, and y =
−1
1
.
(a) Compute Ax and Ay.
(b) Draw the four vectors x, y, Ax, and Ay together on the coordinate plane. One of
x and y is an eigenvector of A – which one? What is the corresponding eigenvalue?
-10 -9 -8 -7 -6 -5 -4 -3 -2 -1
1
2
3
4
5
6
x
y
78
Math 181 Worksheets
W24
6. (a) Let
B =
3 0
0 2
.
What are the eigenvectors and eigenvalues for B? Try figure this out without
making any calculations.
(b) Let
C =
0 −1
1 0
.
Can you find any eigenvalues for C? Why or why not? (Hint: geometrically, what
does the matrix C do to a vector?)
(c) Let
D =
7 −1
6 2
.
Find all the eigenvalues and eigenvectors for D.
79
Math 181 Review Worksheets
R1
1 Review for first midterm
1. Let g(x) =
Z
x
0
cos(t)
t
dt.
(a) Is g(x) increasing or decreasing on 0 < x <
π
2
?
(b) What about on
π
2
< x < π?
2. Compute the following derivatives.
(a)
d
dx
Z
x
3
0
3
√
t
ln(t)
dt
(b)
d
dx
Z
0
x
2
dt
t
80

Math 181 Review Worksheets
R1
3. Compute the following integrals.
(a)
Z
2
0
4x
x
2
+ 2
dx
(b)
Z
x
2
ln(x
2
) dx
(c)
Z
π
6
0
sin(3x)
1 + cos(3x)
dx
(d)
Z
x(ln(x))
2
dx
81
Math 181 Review Worksheets
R1
4. Let R be the region bounded by y = 1 − x
4
and y = |x| − 1.
(a) Sketch the region R.
-2 -1 1 2
-2
-1
1
2
x
y
(b) Compute the area of R.
(c) Set up the integral representing the length of the top edge of R. (You don’t need
to evaluate it.)
(d) Set up the integral representing the volume of the solid obtained by rotating the
region R about the line y = −2.
82
Math 181 Review Worksheets
R1
5. A parabolic antenna is formed by rotating the part of the graph of y = x
2
between
x = 0 and x = 3 around the y-axis.
(a) Draw a sketch of the antenna and compute its volume.
(b) A rainstorm fills the antenna with water to a height of 5 m. Assuming water has
a density of 1000 kg/m
3
and the acceleration due to gravity is 9.8 m/s
2
. Set up
the integral representing the work required to pump the water out over the top
of the antenna.
83

Math 181 Review Worksheets
R1
6. Evaluate the following integrals.
(a)
Z
2x
x
2
− 3x − 10
dx
(b)
Z
3x − 4
x
2
− 3x + 2
dx
(c)
Z
sin
2
(x) dx
(d)
Z
sin
2
(x) cos
3
(x) dx
84

Math 181 Review Worksheets
R1
7. Determine whether each the following improper integrals converge or diverge.
(a)
Z
∞
1
4 dx
e
x
(b)
Z
2
1
4x + 2
x
2
+ x − 2
dx
(c)
Z
π
2
0
tan(θ) dθ
85

Math 181 Review Worksheets
R2
2 Review for second midterm
1. Determine if the following sequences converge or diverge. If they converge, find the
limit.
(a)
−
sin(n)
n
∞
n=1
(b)
(−1)
k
√
k − 3
∞
k=4
(c)
n
√
n − 2
∞
n=3
(d)
5 +
k
2
+ 5
2k
2
+ k − 1
∞
k=0
86

Math 181 Review Worksheets
R2
2. Determine if the following series converge or diverge. If they converge, find the sum.
(a)
∞
X
n=0
2
2n+1
5
n
(b)
∞
X
n=0
1
(n + 3)(n + 2)
(c)
∞
X
n=2
n + 1
n − 1
(d)
∞
X
n=2
n + 1
n
2
− 1
87

Math 181 Review Worksheets
R2
3. Determine if the following series converge absolutely, converge conditionally, or diverge.
(a)
∞
X
k=1
(−3)
k
k!
(b)
∞
X
k=0
(−1)
k
√
k
1 + k
2
(c)
∞
X
k=0
(−1)
k
√
k + 1
88
Math 181 Review Worksheets
R2
4. Determine the radius and interval of convergence of the following power series.
(a)
∞
X
n=1
(x + 2)
n
n4
n
(b)
∞
X
k=1
2
k
(x − 3)
k
k
2
5. Use a Taylor polynomial of degree 2 to approximate
√
5.
6. Find a power series representation for
x
3
x + 2
and determine its radius and interval of
convergence.
89

Math 181 Review Worksheets
R2
7. Let f(x) =
∞
X
n=0
x
n
n!
= 1 + x +
x
2
2!
+
x
3
3!
+
x
4
4!
+ ···.
(a) Find a power series representation for g(x) = x
2
f(−x
2
).
(b) Use the first three non-zero terms of the series you found in part (a) to approximate
the definite integral
Z
1
0
g(x) dx.
90
Math 181 Review Worksheets
R3
3 Review for final exam (part one)
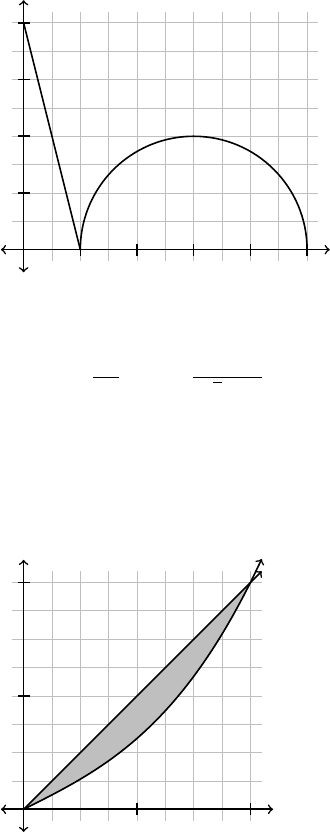
1. The graph of f below consists of a line segment, and a semi-circle of radius 2. Let
g(x) =
Z
x
0
f(t) dt for 0 ≤ x ≤ 5.
1 2 3 4 5
1
2
3
4
x
f(x)
Evaluate g(0), g(1), g(5), and g
0
(3).
2. Compute
d
dx
Z
x
3
1
sin t
√
t + 1
dt
!
.
3. Let R be the region enclosed by y = x
3
+ x and y = 2x with y ≥ 0.
10.5
1
2
x
R
(a) Set up the integral for the area of the
region R.
(b) Set up the integral for the volume of the solid obtained by rotating R about the
line y = −1.
91

Math 181 Review Worksheets
R3
4. Evaluate the following integrals.
(a)
Z
1
0
(6x
2
+ 8x + 6)e
x
3
+2x
2
+3x
dx
(b)
Z
sin(x)
e
cos(x)
dx
(c)
Z
6x
2
+ 4x − 4
x
3
+ x
2
− 2x
dx
(d)
Z
e
1
x
2
ln(x) dx
(e)
Z
arctan(x) dx
(f)
Z
π
2
0
cos
3
(x) dx
92

Math 181 Review Worksheets
R3
5. Find the arc length of the following curves on the given interval.
(a) y =
2
3
x
3
2
on [0, 3].
(b) y = 2 ln x −
x
2
16
on [1, e].
6. Suppose an inverted conical tank with a height of 10 m and a radius of 1 m is filled
completely with paint having a density of 1200 kg/m
3
. Assume the acceleration due
to gravity is 10 m/s
2
.
(a) What is the radius of the tank at a height of h meters?
(b) Set up the integral representing the work required to empty the tank from the
top.
93

Math 181 Review Worksheets
R3
7. For each of the following improper integrals, explain why it is improper and determine
whether the integral converges or diverges.
(a)
Z
3
1
dx
(x − 1)
2
(b)
Z
∞
1
dx
x
2
+ 1
(c)
Z
∞
1
4 dx
e
x
94

Math 181 Review Worksheets
R3
8. In a very wet period of summer, it persistently rained over several days. The precipi-
tation rate P was recorded. It was measured in inches/hour, see the table given below
for a snapshot of one full day. (a) Use Simpson’s Rule, and (b) use the Trapezoidal
Rule to estimate the total amount of precipitation that flooded the town on that day.
t 12 am 6 am 12 pm 6 pm 12 am
P 100 120 90 90 10
Use the following rules to estimate the total amount of precipitation that flooded the
town on this day.
(a) Simpson’s rule
(b) Trapezoidal rule
(c) Midpoint rule (Use two subintervals.)
9. Use the trapezoid rule with 3 sub-intervals to estimate
Z
3
0
x
3
dx.
95

Math 181 Review Worksheets
R4
4 Review for final exam (part two)
1. Determine whether the following statements are true or false. Explain the reasoning
behind your answer.
(a) The series
∞
X
n=1
a
n
diverges if lim
n→∞
S
n
= 5 where S
n
=
n
X
k=1
a
k
.
(b) If the series
∞
X
n=1
a
n
converges, then the series
∞
X
n=1
|a
n
| converges.
(c) The series
∞
X
n=1
1
√
n
converges.
(d) If lim
n→∞
a
n
= 0, then the series
∞
X
n=1
a
n
converges.
(e) If the series
∞
X
n=1
a
n
converges then lim
n→∞
a
n
= 0.
2. Determine whether the series
∞
X
n=2
(−1)
n
ln n
converges absolutely, conditionally or diverges.
Justify you response. That is, state the name of any test you are using and verify that
the conditions of the test are satisfied.
96

Math 181 Review Worksheets
R4
3. Determine whether the following series converge or diverge. If the series converges,
compute its sum.
(a)
∞
X
n=1
e
1/n
− e
1/(n+1)
(b)
∞
X
n=1
3n
2
+ 1
4n
2
− 3
(c)
∞
X
n=1
(−4)
n
3
2n+2
4. Find the radius and the interval of convergence for the following power series.
∞
X
k=1
(−1)
k+1
(x − 1)
k
k3
k
97
Math 181 Review Worksheets
R4
5. (a) Find the 3rd-degree Taylor polynomial of f(x) = e
x
centered at x = 0.
(b) Use your results from part (a) to approximate
10
√
e. You do not need to simplify
your answer.
6. (a) Find a power series representation for f(x) =
1
1 + x
3
.
(b) Find a power series representation for g(x) =
x
1 + x
3
.
(c) Use your result in part (b) to approximate the indefinite integral
Z
x
1 + x
3
dx.
7. Let f(x) =
∞
X
k=1
(−1)
k+1
x
k
k
2
= x −
x
2
4
+
x
3
9
−
x
4
16
+ ···.
(a) Find the first three non-zero terms of the power series representing the function
g(x) = f (x
4
).
(b) Use your results in part (a) to approximate the indefinite integral:
Z
g(x) dx.
98
Math 181 Review Worksheets
R4
8. Given the parametric equation x = 2 cos(t) and y = sin(t) for 0 ≤ t ≤ 2π.
(a) Sketch a graph of the curve.
-2 -1 1 2
-1
1
x
y
(b) Find the slope of the tangent line at t =
3π
4
.
9. Find the Cartesian coordinates of the point on the polar curve r = 2 + 4 cos(θ) at
θ =
2π
3
.
99
Math 181 Review Worksheets
R4
10. Let A =
1 2
1 0
, v
1
=
0
1
, v
2
=
1
−1
, v
3
=
1
1
, and v
4
=
2
1
.
(a) Compute Av
1
, Av
2
, Av
3
, and Av
4
.
(b) Which of these vectors are eigenvectors of A? What are their corresponding
eigenvalues?
(c) Sketch the eigenvectors and their corresponding images under the matrix A.
-4 -3 -2 -1 1 2 3 4
-2
-1
1
2
x
y
(d) Solve for x in Ax =
1
3
by first finding A
−1
.
100
Index
absolute convergence, 45
alternating series test, 45
antiderivative, 4
applications, 45
approximation, 45
arc length, 19
arcs, 59
area, 13, 16
area of compound
regions, 13
area under curve, 1
augmented matrix , 66
average value, 7
Cartesian coordinates, 62
Cartesian-to-polar
method, 62
circles, 59
circular motion, 59
combining power series,
49
comparison test, 42
conditional convergence,
45
convergence, 33, 36
definite integral, 1, 4, 23
determinants, 69, 72
differentiating power
series, 49
divergence, 33, 36
divergence test, 39
eigenvalues, 76
eigenvectors, 76
ellipses, 59
even functions, 7
exponential functions, 10
factoring, 29
Fundamental Theorem of
Calculus, 4
geometric series, 36, 39
harmonic series, 39
identity map, 76
improper integral, 29
indefinite integral, 4, 23
infinite intervals, 29
infinite limit of
integration, 29
infinite series, 36
integrating power series,
49
integration, 1, 4, 7, 10
integration by parts, 23,
26
interval of convergence,
49
inverse matrix, 69, 72
length of curves, 19
limit comparison test, 42
limits of sequences, 33
linear approximation, 45
linear maps, 76
linear systems, 66, 69, 72
long division, 29
Maclaurin series, 56
matrix, 66
matrix multiplication, 66
midpoint rule, 53
numerical integration, 53
odd functions, 7
p-test, 39
parametric equations, 59
partial fractions, 29
partial sums, 36
physical applications, 19
polar coordinates, 62
polar curves, 62
polynomials, 29
power series, 45, 49
pumps, 19
quadratic approximation,
45
radius of convergence, 49
ratio-test, 39
recursive sequences, 33
region between curves,
13, 16
Riemann sum, 1
rotations, 76
sequences, 33
series, 36, 39, 42, 45
series approximation, 56
series expansion, 56
Simpson’s rule, 53
slicing method, 13, 16
slope, 59
solid of revolution, 16
springs, 19
substitution, 10
symmetric functions, 7
symmetry, 7
system of equations, 66
Taylor polynomials, 45
Taylor series, 56
telescoping series, 36
trapezoid rule, 53
trigonometric functions,
10, 26
trigonometric integration,
26
unbounded integrands, 29
vectors, 76
volume, 13, 16
work, 19
