Searching for the Reference Point
AURÉLIEN BAILLON, HAN BLEICHRODT, AND VITALIE SPINU
Erasmus School of Economics,
Erasmus University Rotterdam, The Netherlands
May 2017
Abstract
This paper explores empirically how people form their reference point in decision
under risk. Reference-dependence plays a key role in explaining people’s choices, but
reference-dependent theories, like prospect theory, leave the reference point
unspecified. We assume a comprehensive reference-dependent model that nests the
main reference-dependent theories and that allows isolating the reference point rule
from the other behavioral parameters. We estimate the (posterior) probability that
subjects use a specific reference point rule by Bayesian hierarchical modeling. Our
experiment involved high stakes with payoffs up to a weekly salary. The most common
reference points were the status quo and a security level (the maximum of the minimal
outcomes of the prospects in a choice). Twenty percent of the subjects used an
expectations-based reference point as in the influential theory of Köszegi and Rabin
(2006, 2007).
Key words: reference point formation, reference-dependence, Bayesian hierarchical
modeling, large-stake experiment.
JEL code: D81, C91.
1

Introduction
A key insight of behavioral economics is that people evaluate outcomes as gains and
losses from a reference point. Reference-dependence is central in prospect theory, the
most influential theory of decision under risk, and it plays a crucial role in explaining
people’s attitudes towards risk (Rabin 2000; Wakker, 2010). Evidence abounds, from
both the lab and the field, that preferences are reference-dependent.
1
A fundamental problem of prospect theory and other reference-dependent theories
is that they are silent about how reference points are formed. Back in 1952, Markowitz
(1952) already remarked about customary wealth, which plays the role of the reference
point in his analysis, that “It would be convenient if I had a formula from which
customary wealth could be calculated when this was not equal to present wealth. But I
do not have such a rule and formula (p.157).” This silence is undesirable as it creates
too much freedom in deriving predictions, making it impossible to rigorously test
reference-dependent theories empirically.
2
Reviewing the literature, more than 60
years after Markowitz, Barberis (2013) concludes that addressing the formation of the
reference point is still a key challenge to apply prospect theory to economics (p.192).
The leading theory of reference point formation was proposed by Köszegi and Rabin
(2006, 2007). They argue that the reference point is determined by people’s (rational)
expectations. Köszegi and Rabin’s model for the first time made the reference point
1
Examples of real-world evidence for reference-dependence are the equity premium puzzle, the
finding that stock returns are too high relative to bond returns (Benartzi and Thaler 1995), the
disposition effect, the finding that investors hold losing stocks and property too long and sell winners too
early (Odean 1998, Genesove and Mayer 2001), default bias in pension and insurance choice (Samuelson
and Zeckhauser 1988, Thaler and Benartzi 2004) and organ donation (Johnson and Goldstein 2003), the
excessive buying of insurance (Sydnor 2010, the annuitization puzzle, the fact that at retirement people
allocate too little of their wealth to annuities (Benartzi et al. 2011), the behavior of professional golf
players (Pope and Schweitzer 2011) and poker players (Eil and Lien 2014), and the bunching of
marathon finishing times just ahead of round numbers (Allen et al. forthcoming).
2
For example, different assumptions about the reference point are required to explain two well-
known anomalies from finance: the equity premium puzzle demands that the reference point adjusts over
time, whereas adjustments in the reference point weaken the disposition effect (Meng and Weng
forthcoming).
2

operational and gave testable implications. It is close in spirit to the disappointment
models of Bell (1985), Loomes and Sugden (1986), Gul (1991), and Delquié and Cillo
(2006) in which decision makers also form expectations about uncertain prospects and
experience elation or disappointment depending on whether the actual outcome is
better or worse than those expectations.
3
Empirical evidence on the formation of reference points is scarce and what is
available gives mixed conclusions. Some evidence is consistent with Köszegi and Rabin’s
model of expectations-based reference points (Abeler et al. 2011, Card and Dahl 2011,
Crawford and Meng 2011, Gill and Prowse 2012, Bartling et al. 2015), but other
evidence is not (e.g. Baucells et al. 2011, Allen et al. forthcoming, and Lien and Zheng
2015). Moreover, evidence that has been interpreted as supporting Köszegi and Rabin’s
model may not necessarily exclude other reference point rules.
4
Barberis (2013)
concludes that in finance there are “natural reference points other than expectations.”
Evidence from medical decision making suggests that, instead of using an expectations-
based reference point, people adopt the MaxMin rule described above to determine
their reference point (Bleichrodt et al. 2001, van Osch et al. 2004, van Osch et al. 2006).
This paper explores the formation of reference points in decision under risk. We
performed an experiment in Moldova, an Eastern European country, with large stakes
up to a weekly salary. Guided by the available literature, we specified six reference point
rules, including two expectations-based reference point rules, MaxMin, and the status
quo, which is often used as a reference point in experiments. The selected rules vary
depending on whether they are choice-specific (the reference points is determined by
3
Other models of reference point formation were proposed by Heath et al. (1999), who suggested
that people use goals as their reference points and by Diecidue and Van de Ven (2008), who presented a
model with an aspiration level, which is a form of reference dependence.
4
To illustrate, in the online Appendix we show that the data of Abeler et al. (2011) are also consistent
with MaxMin, a security-based rule according to which subjects adopt the maximum outcome that they
can reach for sure as their reference point.
3
the choice set) or prospect-specific (the reference point is determined by the prospect
itself), stochastic or deterministic, and on whether they are defined only by the outcome
dimension or by both the outcome and the probability dimension.
All the reference points that we consider can be identified through choices. Hence,
we work within the revealed preference paradigm and do not require introspective
data. In this we follow Rabin (2013) approach to develop more realistic theories that
are maximally useful to core economic research. Rabin argues that new models should
be “portable” and use the same independent variables as existing models. The core
economic model of decision under risk is expected utility, which uses probabilities and
outcomes as independent variables. Tversky and Kahneman’s (1992) prospect theory is
not portable because it leaves the reference point unspecified. By contrast, all our
reference point rules can be derived from probabilities and outcomes and are portable.
We define a comprehensive reference-dependent model that includes the main
reference-dependent theories as special cases. This makes it possible to compare
reference point rules ceteris paribus, i.e. to isolate the reference point rule from the
specification of the other behavioral parameters like utility curvature, probability
weighting, and loss aversion. We use a Bayesian hierarchical model to estimate each
subject’s reference point rule. Bayesian hierarchical modeling estimates the parameters
of each individual separately, but accounts for their similarities in the population. This
leads to more precise estimates and prevents inference from being dominated by
outliers (Rouder and Lu 2005, Nilsson et al. 2011).
Our results indicate that two reference point rules stand out: the status quo and
MaxMin. Together these two reference points account for the behavior of over sixty
percent of our subjects. Around twenty percent of our subjects use an expectations-
based reference point rule.
4
1. Theoretical background
A prospect is a probability distribution over money amounts. Simple prospects assign
probability 1 to a finite set of outcomes. We denote these simple prospects as
(
,
; … ;
,
), which means that they pay €
with probability
, = 1, … , . We
identify simple prospects with their cumulative distribution functions and denote them
with capital Roman letters (,). The decision maker has a weak preference relation
over the set of prospects and, as usual, we denote strict preference by , indifference by
, and the reversed preferences by and . The function defined from the set of
simple prospects to the reals represents if for all prospects , , ()
().
Outcomes are defined as gains and losses relative to a reference point . An outcome
is a gain if > and a loss if < .
1.1. Prospect theory
Under prospect theory (Tversky and Kahneman 1992), there exist probability
weighting functions
and
for gains and losses and a non-decreasing gain-loss
utility function : with
(
0
)
= 0 such that preferences are represented by
(
)
=
()
(1 )
+
( )
()
. (1)
The integrals in Eq. (1) are Lebesgue integrals with respect to distorted measures
(1 ) and
(). For losses, the weighting applies to the cumulative distribution
(), for gains to the decumulative distribution (1 ).
The functions
and
are non-decreasing and map probabilities into [0,1] with
(
0
)
= 0,
(
1
)
= 1, = +, . When the
are linear, reduces to expected utility
with referent-dependent utility:
(
)
=
(
)
. (2)
5
Equation (2) shows that reference-dependence by itself does not violate expected utility
as long as the reference point is held fixed.
Based on empirical observations, Tversky and Kahneman (1992) hypothesized
specific shapes for the functions ,
, and
. The gain-loss utility is S-shaped,
concave for gains and convex for losses. It is steeper for losses than for gains to capture
loss aversion, the finding that losses loom larger than gains. The probability weighting
functions are inverse S-shaped, reflecting overweighting of small probabilities and
underweighting of middle and large probabilities.
1.2. Köszegi and Rabin’s model
Tversky and Kahneman (1992) defined prospect theory for a riskless reference
point . Köszegi and Rabin (2006, 2007) added two elements to prospect theory. First,
they distinguished the economic concept of consumption utility and the psychological
concept of gain-loss utility and, second, they allowed for stochastic reference points. Let
be the stochastic reference point. In Köszegi and Rabin’s model preferences over
prospects are represented by
(
)
=
(
)
+
(
)
(
)
. (3)
In Eq. (3), represents consumption utility, which does not depend on the reference
point, but only on the absolute size of the payoffs. is the gain-loss utility function,
which depends on the reference point and reflects the psychological part of utility.
Köszegi and Rabin (2007, p.1052) argue that “for modest-scale risk, such as $100
or $1000,[…] consumption utility can be taken to be approximately linear”. Linear
consumption utility is also commonly assumed in empirical applications of Köszegi and
Rabin’s model (e.g. Heidhues and Kőszegi 2008, Abeler et al. 2011, Gill and Prowse
2012, Eil and Lien 2014). As the incentives in our experiment did not exceed $100 (in
6
PPP) and the prospects in the different choice sets had approximately equal expected
value, we concentrate on the gain-loss function and take
(
)
= :
(
)
=
+
(
)
. (4)
There is no probability weighting in Eq. (4). It is unclear how the rational
expectations reference point should be defined in the presence of probability weighting.
Köszegi and Rabin (2006, 2007) do not address this problem and leave out probability
weighting, even though they acknowledge its relevance (Köszegi and Rabin 2006,
footnote 2, p. 1137).
While prospect theory does not specify the reference point, Köszegi and Rabin
(2007) present a theory in which reference points are determined by the decision
maker’s rational expectations. They distinguish two specifications of the reference
point, one prospect-specific and one choice-specific. In a “choice-acclimating personal
equilibrium” (CPE), the reference point is the prospect itself. This prospect-specific
reference point gives:
(
)
=
+
(
)
. (5)
In a choice-unacclimating personal equilibrium (UPE), the reference point is choice-
specific and is equal to the preferred prospect in the choice set.
1.3. Disappointment models
Köszegi and Rabin’s (2006, 2007) model is close to the disappointment models of
Bell (1985), Loomes and Sugden (1986), Gul (1991), and Delquié and Cillo (2006). Bell’s
model is equivalent to Eq. (3) with () replaced by the expected consumption value of
the prospect (although Bell remarks that this may be too restrictive and also presents a
more general model), Loomes and Sugden’s model (1986) is equivalent to Eq.(3) with
7

() replaced by the expected consumption utility of the prospect,
5
and Gul’s (1991)
model is equivalent to Eq.(3) with () replaced by the certainty equivalent of the
prospect. Delquié and Cillo‘s (2006) model is identical to Köszegi and Rabin’s (2007)
CPE model (Eq. 5). Masatlioglu and Raymond (2016) formally characterize the link
between Köszegi and Rabin’s (2007) CPE model, the disappointment models, and other
generalizations of expected utility. They show that if the gain-loss utility function is
linear and the decision maker satisfies first-order stochastic dominance, CPE is equal to
the intersection between rank-dependent utility (Quiggin 1981, Quiggin 1982) and
quadratic utility (Machina 1982, Chew et al. 1991, Chew et al. 1994).
2.4 General reference-dependent specification
This paper compares the performance of different reference point rules in
explaining behavior. To isolate the reference point, we must use the same model
specification across all reference point rules and, consequently, all other behavioral
parameters must enter the same way. To address this ceteris paribus principle we adopt
the following general reference-dependent model:
(
)
=
+
(
)
. (6)
Eq. (6) contains prospect theory (Eq. 1), Köszegi and Rabin’s (2006, 2007) model
(Eq. 4) and the disappointment models as special cases. In Eq. (6), probability weighting
plays a role in the psychological part of the model (the second term of the addition), but
it does not affect consumption utility (the first term). This seems reasonable as
consumption utility reflects the “rational” part of utility and probability weighting is
usually considered irrational. Adjusting the model to also include probability weighting
in consumption utility is straightforward.
5
With consumption utility .
8

Probability weighting does not affect the formation of reference points either. In this
we follow the literature on stochastic reference points (Sugden 2003, Delquié and Cillo
2006, Köszegi and Rabin 2006, Köszegi and Rabin 2007, Schmidt et al. 2008). We will
consider alternative specifications in Section 6.4.
2. Reference point rules
A reference point rule specifies for each choice situation which reference point is
used. Table 1 summarizes the reference point rules that we studied. We distinguish
reference point rules along three dimensions. First, whether they are prospect-specific
and determine a reference point for each prospect separately, or choice-specific and
determine a common reference point for all prospects within a choice set. Second,
whether they determine a stochastic or a deterministic reference point. Third, whether
they use only the payoffs to determine the reference point or both payoffs and
probabilities.
Prospect Specific
Stochastic
Uses probability
Status Quo
Choice
No
No
MaxMin
Choice
No
No
MinMax
Choice
No
No
X at Max P
Choice
No
Yes
Expected Value
Prospect
No
Yes
Prospect Itself
Prospect
Yes
Yes
Table 1. The reference point rules studied in this paper
The first reference point rule is the Status Quo, which is often used in experimental
studies of reference-dependence. Our subjects knew that they would receive a
participation fee for sure. Consequently, we took the participation fee as the status quo
reference point and any extra money that subjects could win if one of their choices was
played out for real as a gain. Expected utility maximization is the special case of Eq.(6)
9

with the status quo as the reference point where subjects do not weight probabilities
(expected utility). Expected value maximization is the special case of expected utility
with the status quo as the reference point where subjects have linear utility.
MaxMin, the second reference point rule, is based on Hershey and Schoemaker
(1985). They found that when asked for the probability that made them indifferent
between outcome for sure and a prospect (,
; 1 ,
), their subjects took as
their reference point and perceived
as a gain and
as a loss. Bleichrodt et al.
(2001) and van Osch et al. (2004, 2006, 2008) found similar evidence for such a strategy
in medical decisions. For example, van Osch et al. (2006) asked their subjects to think
aloud while choosing. The most common reasoning in a choice between life duration
for sure and a prospect (,
; 1 ,
) was: “I can gain years if the gamble goes
well or lose if it doesn’t.”
MaxMin generalizes the above line of reasoning to the choice between any two
prospects.
6
It posits that in a comparison between two prospects, people look at the
minimum outcomes of the two prospects and take the maximum of these as their
reference point. This reference point is the amount they can obtain for sure. For
example, in a comparison between (0.50,100; 0.50,0) and (0.25,75; 0.75,25), the
minimum outcomes are 0 and 25, and because 25 exceeds 0, MaxMin implies that
subjects take 25 as their reference point.
MaxMin is a cautious rule and implies people are looking for security. MinMax is the
bold counterpart of MaxMin. A MinMax decision maker looks at the maximal
opportunities and takes the minimum of the maximum outcomes as his reference point.
6
To the best of our knowledge this rule was first proposed in Bleichrodt and Schmidt (2005). See also
Birnbaum and Schmidt (2010) and Schneider and Day (forthcoming).
10

Hence, MinMax predicts that the decision maker will take 75 as his reference point
when choosing between (0.50,100; 0.50,0) and (0.25,75; 0.75,25).
The MaxMin and the MinMax rules both look at extreme outcomes. One reason is
that these outcomes are salient. Another salient outcome is the payoff with the highest
probability and our next rule, X at MaxP, uses this outcome as the reference point. The
importance of salience is widely-documented in cognitive psychology (Kahneman
2011). Barber and Odean (2008) and Chetty et al. (2009) show the effect of salience on
economic decisions. Bordalo et al. (2012) present a theory of salience in decision under
risk.
The final two reference points that we considered are the expected value of the
prospect, as in the disappointment models of Bell (1985) and Loomes and Sugden
(1986)
7
and the prospect itself as in Köszegi and Rabin’s (2007) CPE model and Delquié
and Cillo’s (2006) disappointment model. Unlike the other reference points, these
reference points are prospect-specific. The prospect itself is the only rule that specifies a
stochastic reference point. If the prospect itself is the reference point then the decision
maker will, for example, reframe the prospect (0.50,100; 0.50,0) as a 25% chance to
gain 100 (if he wins 100 and 0 is the reference point, the probability of this happening is
0.50 0.50 = 0.25), a 25% chance to lose 100 (if he wins nothing and 100 is the
reference point) and a 50% chance that he wins or loses nothing (if he either wins 100
and 100 is the reference point or he wins nothing and nothing is the reference point).
The decision maker’s gain-loss utility is then
(.25)
(
100
)
+
(.25)
(
100
)
.
Two points are worth making. First, Köszegi and Rabin (2007) propose the CPE
model to describe choices with large time delays between choice and outcome, like for
example in insurance decisions. We use it outside this specific context, as did others
7
The equivalence with Loomes and Sugden (1986) follows because we assume
(
)
= .
11
before us (e.g. Rosato and Tymula 2016), because it is tractable, both theoretically and
empirically. Hence, our results do not directly test the CPE model the way it was
conceived. Second, we do not consider the rule that specifies that the preferred prospect
in a choice is used as the reference point, as in Köszegi and Rabin’s (2007) UPE model,
because the model in Eq. (6) is then defined recursively and could not be estimated.
3. Experiment
Subjects and payoffs
The subjects were 139 students and employees from the Technical University of
Moldova (49 females, age range 17-47, average age 22 years). They received a 50 Lei
participation fee (about $4, which was $8 in PPP at the time of the experiment). To
incentivize the experiment, each subject had a one third chance to play out one of their
choices for real.
The payoffs were substantial. The subjects who played out their choices for real
earned 330 Lei on average, which was more than half the average weekly salary in
Moldova at the time of the experiment. Two subjects won about 600 Lei, the average
weekly salary.
Procedure
The experiment was computer-run in group sessions of 10 to 15 subjects. Subjects
took 30 minutes on average to complete the experiment including instructions.
Subjects made 70 choices in total. The 70 choices are listed in Appendix A
including the reference points predicted by each of the rules. The different rules
predicted widely different reference points and the predicted reference points varied
substantially across choices (except of course for the status quo).
12

Each choice involved two options, Option 1 and Option 2. The options had between
one and four possible outcomes, all strictly positive. We randomized the order of the
choices and we also randomized whether a prospect was presented as Option 1 or as
Option 2.
Choices were created by an optimal design procedure that minimized their joint
correlation. Just like orthogonal covariates in linear regression, minimally correlated
choices lead to more precise and more robust estimates of the behavioral parameters.
The optimal design procedure is described in Appendix B.
Figure 1. Presentation of the choices in the experiment
Figure 1 shows the display of the choices. Prospects were presented as
horizontal bars with as many parts as there were different payoffs. The size of each part
corresponded with the probability of the payoff. The intensity of the color (blue) of each
part increased with the size of the payoff. The payoffs were presented in increasing
13
order. Subjects were asked to click on a bullet to indicate their preferred option (Figure
1 illustrates a choice for Option 2).
4. Bayesian hierarchical modeling
We analyzed the data using Bayesian hierarchical modeling. Economic analyses of
choice behavior usually estimate models either by pooling all data or by individual
estimation. Both approaches have their limitations. Pooling ignores individual
heterogeneity and may result in estimates that are not representative of any individual
in the sample. Individual-level estimation relies on relatively few data points, which
may lead to unreliable results. Bayesian hierarchical modeling is an appealing
compromise between these two extremes. It estimates the model parameters for each
subject separately, but it assumes that subjects share similarities and that their
individual parameter values come from a common (population-level) distribution.
Hence, the parameter estimates for one individual benefit from the information that is
obtained from all others. This improves the precision of the estimates (in Bayesian
statistics this is known as collective inference) and it reduces the impact of outliers.
Individual parameters are shrunk towards the group mean, an effect that is stronger for
individuals with noisier behavior, thus making the overall estimation more robust. This
is particularly true for parameters that are estimated with lower precision. An example
is the loss aversion coefficient in prospect theory, for which the standard deviation of
the parameter estimates is usually high. Nilsson et al. (2011) illustrate that Bayesian
hierarchical modeling leads to more accurate and more efficient estimates of loss
aversion than the commonly-used maximum likelihood estimation.
14
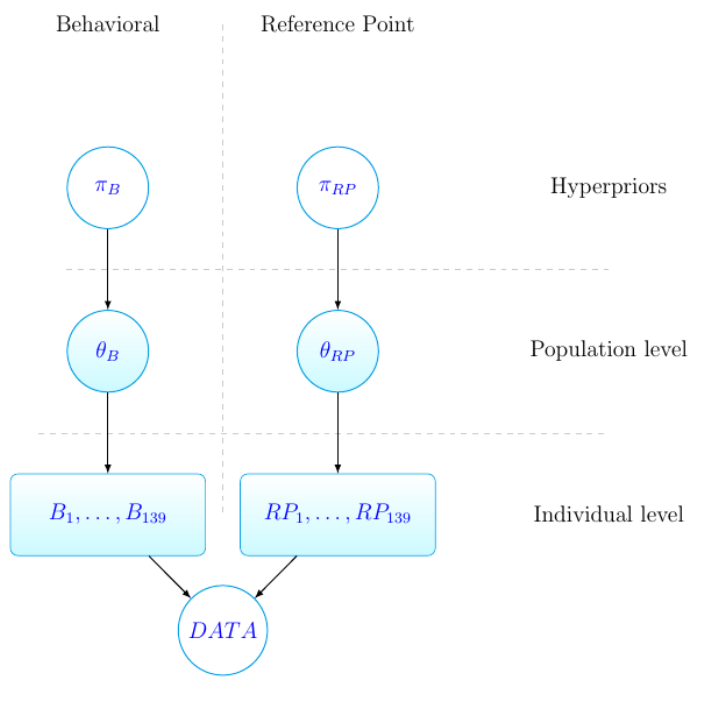
Figure 2 shows a schematic representation of our statistical model. The model
consists of two parts: the specification of the behavioral parameters in Eq. (6), utility
and probability weighting, and the specification of the reference point rule.
Figure 2. Graphical representation of our model.
Non-shaded nodes are known or predefined quantities, shaded nodes are the unknown
latent parameters.
We adopt the following mnemonic conventions. For individual {1, … , 139} the
vector of behavioral parameters is denoted
and his reference point rule is denoted
. We assume that a subject uses the same reference point rule in all choices, where
the reference point rule is one of the candidates listed in Table 1. This may appear
15
restrictive as subjects could use a mixture of reference point rules. Our analysis will
estimate the posterior probabilities of the subjects using each of the different reference
point rules. In that sense, our analysis does allow for the possibility that subjects use a
mixture of reference point rules.
The distributions of the behavioral parameters and the reference point rules in the
population are parameterized by unknown vectors
and
, respectively. Both
and
are estimated from the data. The parameters
and
also follow a
distribution, but with a known shape. This final layer in the hierarchical specification is
commonly referred to as a hyper prior. The hyper priors are denoted by
and
respectively. The vector of the observed choices (data) of the individual is denoted by
= (
, … ,
) . We will now describe our estimation procedure.
5.1. Specification of the behavioral parameters
We assume that the utility function in Eq. (6) is a power function:
(
)
=
( )
( )
<
. (7)
In Eq. (7) reflects the curvature of utility and indicates loss aversion. We
assumed the same curvature for gains and losses. It is hard to estimate loss aversion
when utility curvature for gains and for losses can both vary freely (Nilsson et al. 2011).
For probability weighting, we assumed Prelec‘s (1998) one-parameter specification:
(
)
= exp ((ln )
). (8)
We used the same probability weighting for gains and losses. Empirical studies
usually find that the differences in probability weighting between gains and losses are
relatively small (Tversky and Kahneman 1992, Abdellaoui 2000, Kothiyal, Spinu, and
Wakker, 2014).
16

To account for the probabilistic nature of people’s choices we used Luce‘s (1959)
logistic choice rule. Let () and () denote the respective values of prospects
and according to our general reference-dependent model, Eq. (6). Luce’s rule says that
the probability (, ) of choosing prospect over prospect equals
(
,
)
=
[
(
)
()
]
. (9)
In Eq. (9), > 0 is a precision parameter that measures the extent to which the
decision maker’s choices are determined by the differences in value between the
prospects. In other words, the -parameter signals the quality of the decision. Larger
values of imply that choice is driven more by the value difference between prospects
and . If = 0, choice is random and if goes to infinity choice essentially becomes
deterministic. In his comprehensive exploration of prospect theory specifications, Stott
(2006) concluded that power utility, the Prelec one-parameter probability weighting
function, and Luce’s choice rule gave the best fit to his data. We, therefore, selected
these specifications.
To test for robustness, we also ran our analysis with exponential utility, Prelec’s
(1998) two-parameter specification of the weighting function, and an alternative,
incomplete beta (IBeta) probability weighting function (Wilcox 2012). IBeta is a flexible,
two parameter family that can accommodate many shapes (convex, concave, s-shaped
and inverse s-shaped) (see Appendix C and the online Appendix for details). The
robustness analyses confirmed our main conclusions. The results of these analyses are
in the online appendix.
Each of the 139 subjects in the experiment had his own parameter vector
=
(
,
,
,
). We assumed that each parameter in
comes from a lognormal
distribution:
~(
,
),
~(
,
),
~(
,
), and
~(
,
).
17
Thus, the complete vector of unknown parameters at the population-level is
=
,
,
,
,
,
,
,
. For the hyper-priors,
=
(
,
)
, {, , , } of the
parent distributions we made the usual assumption that the
follow a lognormal
distribution and that the
follow an inverse Gamma distribution. We centered the
hyper-priors at linearity (expected value) and chose the variances such that the hyper-
priors were diffuse and would have a negligible impact on the posterior estimation.
The joint probability distribution of the behavioral parameters = (
, … . ,
)
and
is
(
,
|
)
=
(
(
|
)
)
(
|
). (10)
Given reference point rule
, the likelihood of subject ’s responses is
(
|
,
) =
,
|
,
. (11)
The probability of each choice
,
is computed using Luce’s rule, Eq.(9). From Eqs.
(10) and (11), it follows that the joint probability distribution of all the unknown
behavioral parameters and
and all the observed choices = (
, … ,
) is
(, ,
|
,
) =
,
|
,
(
(
|
)
)
(
|
)
. (12)
In Eq.(12), = (
, … ,
) is the vector of individual reference point rules.
5.2. Specification of the reference point rule
We assume that subjects use one of the six reference point rules in Table 1. For each
of these rules, we estimated the posterior probability that a subject used it given the
data: (
|
).
is a (six-dimensional) categorical variable for which it is common to
use the Dirichlet distribution:
~
(
)
, where
is a probability vector in
a six-dimensional simplex and
is a diffuse hyper prior parameter for the Dirichlet
distribution. Then the joint probability density of and
becomes:
18

(
,
|
)
=
(
(
|
)
)
(
|
)
. (13)
Substituting Eq.(13) into Eq.(12) gives the complete specification of our statistical
model:
(, ,
, ,
|
,
) =
,
|
,
(
(
|
)
)(
(
|
)
)
(
|
)
(
|
)
. (14)
5.3. Estimation
To compute the marginal posterior distributions
(
|
,
,
)
,
(
|
,
,
)
,
(
|
,
,
)
, and
(
|
,
,
)
, we used Markov Chain Monte Carlo (MCMC)
sampling (Gelfand and Smith 1990) with blocked Gibbs sampling.
8
We first used 10,000
burn-in iterations with adaptive MCMC and then 20,000 standard MCMC burn-in
iterations. The results are based on the subsequent 50,000 iterations.
6. Results
6.1. Consistency
To test for consistency, five choices were asked twice. In 68.7% of these repeated
choices, subjects made the same choice. Reversal rates up to one third are common in
experiments (Stott 2006). Moreover, our choices were complex, involving more than
two outcomes and with expected values that were close. Hence, we believe that the
consistency of our data was satisfactory.
8
For the behavioral parameters
, … ,
we used Metropolis-Hasting MCMC with symmetric
normal proposal on the log-scale, for the block
, … ,
we used Metropolis-Hasting MCMC with
uniform proposal, and the group-level blocks
and
were sampled directly from the conjugate
Gamma-Normal and Dirichlet-Categorical distributions, respectively.
19
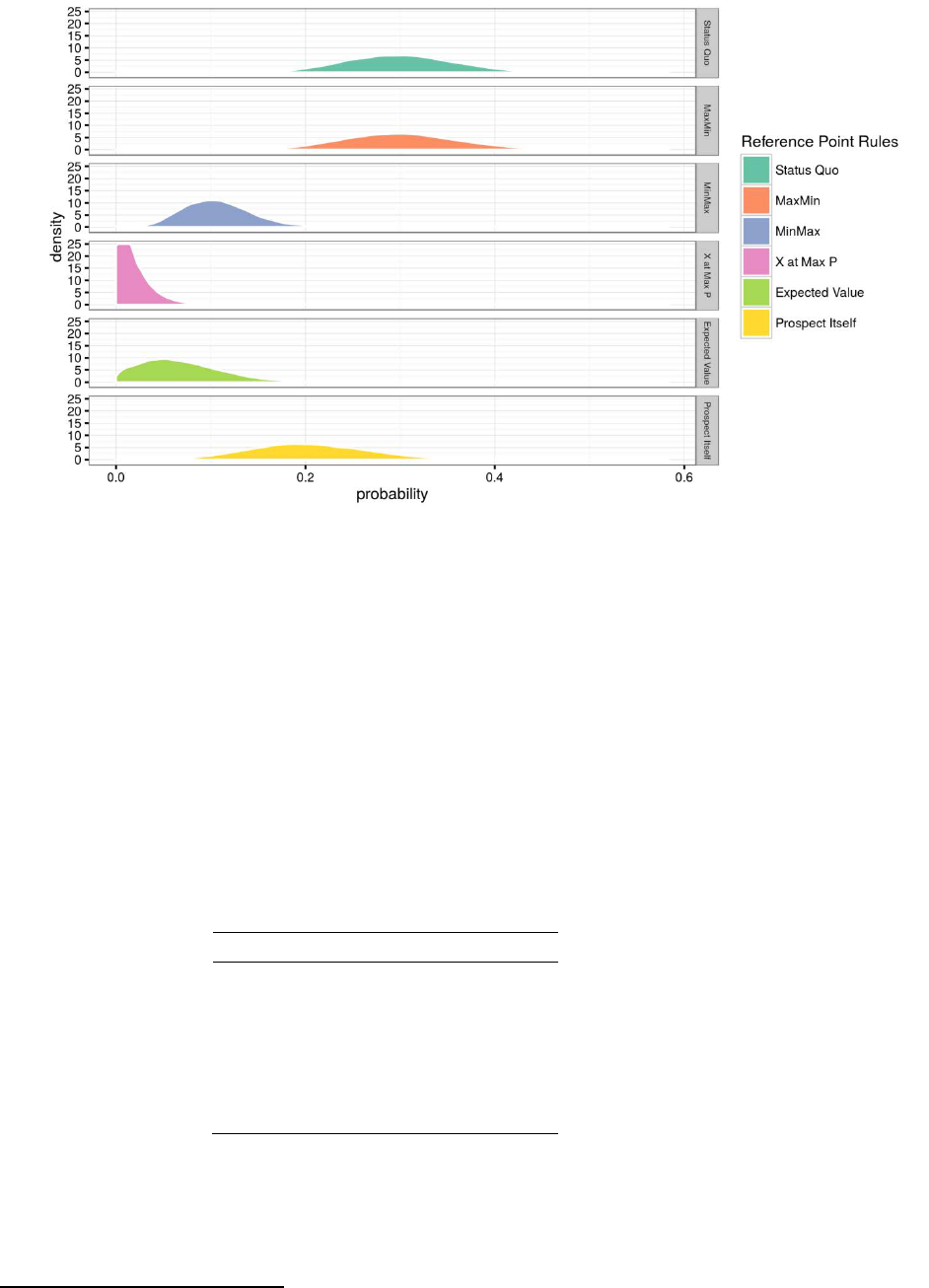
6.2. Reference points
Figure 3. Marginal posterior distributions of each reference point rule
We first report the estimates of
, which indicate for each reference point rule the
probability that a randomly chosen subject behaved in agreement with it. Figure 3
shows for each RP rule the marginal posterior distribution of
in the population.
Table 2 reports the medians and standard deviations of these distributions.
9
Median
SD
Status Quo
0.30
0.06
MaxMin
0.30
0.06
MinMax
0.10
0.04
X at Max P
0.01
0.02
Expected Value
0.06
0.04
Prospect Itself
0.20
0.06
Table 2. Medians and standard deviations of the marginal posterior distributions of
the reference point rules in the population.
9
Note that the medians need not add to 100%.
20
The reference points that were most likely to be used were the status quo and
MaxMin. According to our median estimates, each of these two rules was used by 30%
of the subjects. The prospect itself (the rule suggested by Köszegi and Rabin (2006,
2007) and Delquié and Cillo (2006)) was used by 20% of the subjects. The other three
rules were used rarely.
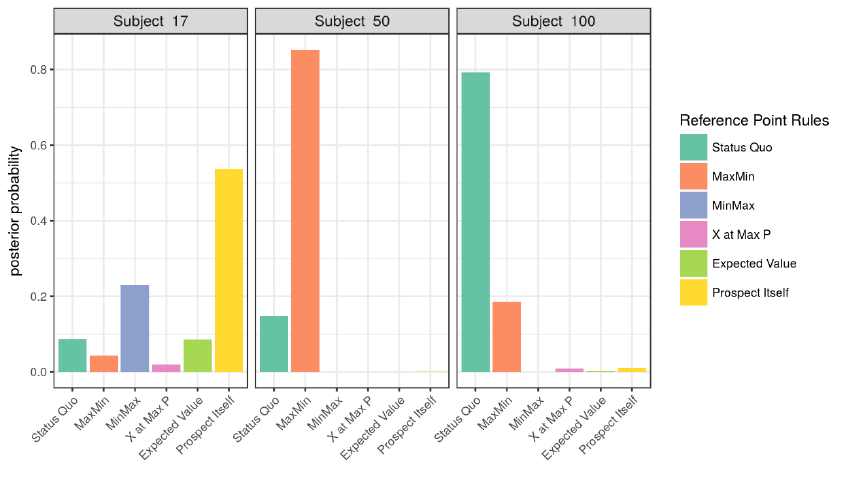
We also estimated for each subject the likelihood he used a specific reference
point by looking at his posterior distribution. Figure 4 shows, for example, the posterior
distributions of subjects 17, 50, and 100. Subject 17 has about 60% probability to use
the prospect itself as his reference point and 25% probability to use the minimum of the
maximums. Subject 50 almost surely uses MaxMin and subject 100 almost surely uses
the status quo as his reference point.
Figure 4. Posterior distributions of subjects 17, 50, and 100.
A subject is classified sharply if he has a posterior probability of at least 50% to
use one of the six reference point rules. For example, subjects 17, 50, and 100 were all
21
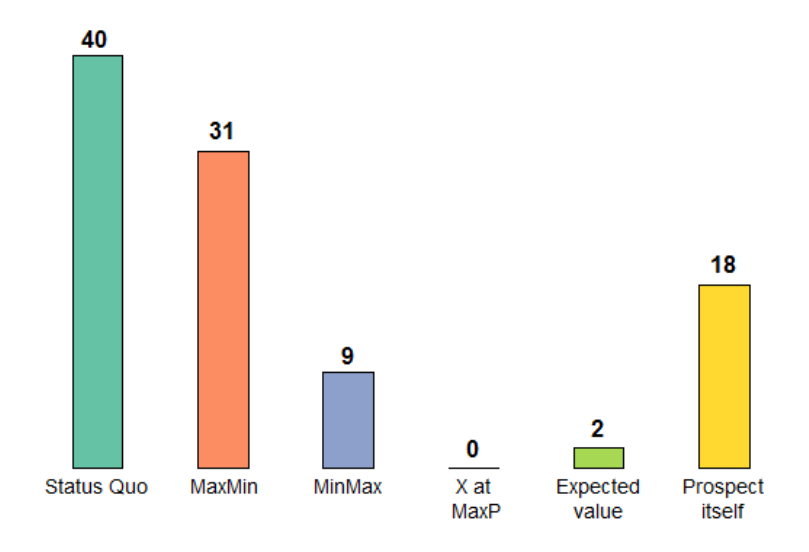
classified sharply. Out of the 139 subjects, 107 could be classified sharply. Figure 5
shows the distribution of the sharply classified subjects over the six reference point
rules. The dominance of the Status Quo and MaxMin increased further and around 70%
of the sharply classified subjects used one of these two rules.
Figure 5. Proportion of sharply classified respondents satisfying a particular
reference point rule (percent)
6.3. Behavioral parameters
Figure 6 shows the gain-loss utility function in the psychological (PT) part of Eq.
(6) based on the estimated behavioral population level parameters (
). The utility
function is S-shaped: concave for gains and convex for losses. We found more utility
curvature than most previous estimations of gain-loss utility (for an overview see Fox
and Poldrack 2014), but our estimated utility function is no outlier. It is, for example,
close to the functions estimated by Wu and Gonzalez (1996), Gonzalez and Wu (1999),
22
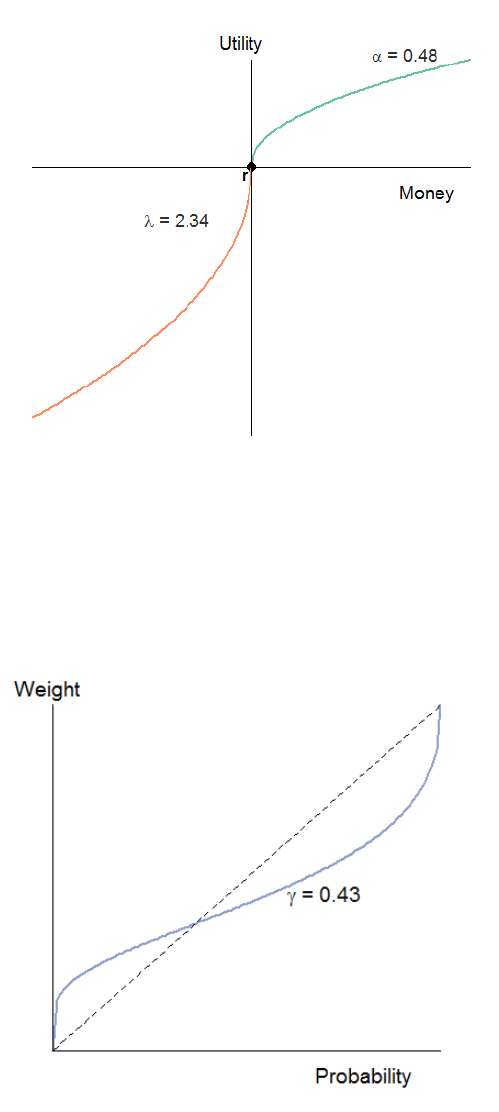
and Toubia et al. (2013). The loss aversion coefficient was equal to 2.34, which is
consistent with other findings in the literature.
Figure 6. The gain-loss utility function based on the estimated group parameters
Figure 7. The probability weighting function based on the estimated group parameters
23
Figure 7 shows the estimated probability weighting function in the population. The
function has the commonly observed inverse S-shape, which reflects overweighting of
small probabilities and underweighting of intermediate and large probabilities.
10
Our
estimated probability weighting function is close to the estimated functions in Gonzalez
and Wu (1999), Bleichrodt and Pinto (2000) and Toubia et al. (2013).
Bayesian hierarchical modeling expresses the uncertainty in the individual
parameter estimates by means of the posterior densities. To illustrate, Figure 8 shows
the posterior densities of subject 17. As the graph shows, subject 17’s parameter
estimates varied considerably, although it is safe to say that he had concave utility and
inverse S-shaped probability weighting.
Figure 8. Posterior densities of the behavioral parameters for subject 17.
10
The Prelec one-parameter probability weighting function only allows for inverse- or S-shaped
weighting. However, the two-parameter Prelec function and the IBeta function allow for all shapes and
their estimated shapes were also inverse S.
24
Table 3 shows the quantiles of the posterior point estimates of all 139 subjects. The
table shows that utility curvature and, to a lesser extent, probability weighting were
rather stable across subjects. Loss aversion varied much more although the estimates of
more than 75% of the subjects were consistent with loss aversion.
2.5%
25%
50%
75%
97.5%
.31
.40
.44
.50
.60
.09
.14
.24
.44
1.66
.36
1.19
1.59
2.25
4.63
6.11
8.26
10.89
14.41
25.76
Table 3. Quantiles of the point estimates of the behavioral parameters of the 139
subjects
Status Quo
.42
.28
1.51
11
11.75
MaxMin
.46
.24
2.24
10.30
MinMax
.40
.15
.50
14.34
Expected Value
.36
.25
2.44
6.14
Prospect Itself
.45
.16
2.23
10.89
Table 4: Median individual level parameters for the sharply classified subjects in each
group.
Table 4 shows the median behavioral parameters of the sharply classified subjects in
each group.
12
A priori, it seemed plausible that subjects who used different rules might
also have different behavioral parameters, in particular loss aversion. The table
confirms this conjecture. While utility curvature and probability weighting were rather
stable across the groups, the loss aversion coefficients varied from 0.50 in the MinMax
group to 2.44 in the Expected Value group. The loss aversion coefficient of 0.50 in the
MinMax group has the interesting interpretation that these optimistic subjects weight
11
The reason that is not equal to 1 for subjects who were sharply classified as using the status quo
rule is that a subject’s behavioral parameters stayed the same for all reference point rules. Consequently,
even when a subject was (sharply) classified as a status quo type, there was still a non-negligible
probability that he used any of the other reference point rules and was loss averse.
12
X at MaxP is not in the table as there were no sharply classified subjects who behaved according to
this rule.
25

gains twice as much as losses and they exhibit what might be seen as the reflection of
the preferences of the cautious MaxMin subjects who weight losses more than twice as
much as gains.
Table 4 also shows that subjects who used the status quo as their reference point
were typically no expected utility maximizers as there was substantial probability
weighting in this group. Table 5 gives a more detailed overview. It shows the
subdivision of the subjects who used the status quo as their reference point based on
the 95% Bayesian credible intervals of their estimated utility curvature and probability
weighting parameters. Twelve subjects (those with = 1) behaved according to
expected utility, three of whom (those with = 1 and = 1) were expected value
maximizers. Thus, less than 10% of our subjects were expected utility maximizers.
Probability weighting
< 1
= 1
> 1
Total
Utility
< 1
28
9
0
37
= 1
3
3
0
9
> 1
0
0
0
0
Total
31
12
0
43
Table 5. Behavioral parameters of the subjects using the status quo as their reference
points (classification into groups is based on the 95% Bayesian credible intervals).
6.4. Robustness
In the main analysis, we assumed Eq. (6) for all reference point rules, allowing us
to keep all behavioral parameters constant when comparing reference point rules. We
also tried several other specifications, which are summarized in Table 6. Model 1
corresponds to the results reported in Sections 6.2 and 6.3. The two variables we varied
in the robustness checks were the inclusion of consumption utility and probability
weighting. While models with prospect-specific reference points need consumption
26

utility to exclude implausible choice behavior,
13
models with a choice-specific reference
point do not. Prospect theory, for example, does not include consumption utility.
Consequently, we estimated the models with a choice-specific reference point both with
and without consumption utility.
Model
Choice-specific reference point
Prospect-specific reference point
Consumption
utility
Probability
weighting
Consumption
utility
Probability
weighting
1
Yes
Yes
Yes
Yes
2
No
Yes
Yes
Yes
3
Yes
Yes
Yes
No
4
No
Yes
Yes
No
5
Yes
No
Yes
No
6
No
No
Yes
No
Table 6: Estimated models
In Eq. (6) we assumed that subjects weight probabilities when they evaluate
prospects relative to a reference point, but, following the literature on stochastic
reference points, we abstracted from probability weighting in the determination of the
stochastic reference point. This may be arbitrary and we, therefore also estimated the
models without probability weighting. We performed two sets of estimations: one in
which the models with a choice-specific reference point included probability weighting,
but the models with a prospect-specific reference point did not (models 3 and 4) and
one in which no model had probability weighting (models 5 and 6).
The results of the robustness checks were as follows. First, our main conclusion
that the status quo and MaxMin were the dominant reference points remained valid.
The behavior of 60% to 75% of the subjects was best described by a model with one of
these two reference points. Second, excluding consumption utility from models with a
13
For example, in Köszegi and Rabin’s (2007) CPE model without consumption utility any prospect
that gives with probability 1 has a value of 0, regardless of the size of . So the decision maker should be
indifferent between $1 for sure and $1000 for sure. Consumption utility prevents this.
27
choice-specific reference point (models 2 and 4) led to a substantial increase in the
precision parameter . This suggests that there is no need to include consumption
utility in models like prospect theory. Third, probability weighting played a crucial role.
Excluding probability weighting from the models with a prospect-specific reference
point (model 3) decreased the share of the prospect itself as a reference point to 10%
(8% if we only include the sharply classified subjects) and increased the share of the
MaxMin reference point to 44% (52% if we only include the sharply classified subjects).
The shares of the other rules changed only little. Hence, prospect-specific models like
Köszegi and Rabin’s (2006, 2007) benefit from including probability weighting. Ignoring
probability weighting altogether, as in models 5 and 6, led to unstable estimation
results.
The behavioral parameters were comparable across all models that we
estimated. The power utility coefficient was approximately 0.50 in all models, the
probability weighting parameter varied between 0.40 and 0.60 (except, of course, when
no probability weighting was assumed), and the loss aversion coefficient varied
between 2 and 2.50. Detailed results of the robustness analysis are in the online
appendix.
6.5 Cross-validation
Throughout the paper we considered 6 reference point rules. Even though these
rules cover many of the rules that have been proposed in the literature and used in
empirical research, it might be that subjects adopted another rule. In that case the
model would be misspecified and would poorly predict subjects’ choices. To explore this
possibility, we performed the following cross-validation exercise. We estimated the
model on 69 questions and predicted the choice made by each of the 139 subjects for
28
the remaining question. This out-of-sample prediction procedure was repeated 70
times, once for each hold-out question. The models predicted around 70% of the choices
correctly. Given that the consistency rate was also around 70%, we conclude that the
rules that we included captured our subjects’ preferences well and that there is no
indication that the model was misspecified. The part that could not be explained
probably reflected noise.
7. Discussion
Empirical studies of decisions under risk that want to account for reference-
dependence often assume that subjects take the status quo as their reference point. In
our data this assumption was justified for 30-40% of the subjects, but a majority used a
different reference point. Our data also suggest how experimental researchers can
increase the likelihood that subjects use the participation fee as their reference point.
For example, in choosing between mixed prospects, researchers could include a
prospect with 0 as its minimum outcome in each choice. This ensures that MaxMin
subjects will also use 0 as their reference point and our results suggest that then a
substantial majority of the subjects will use 0 as their reference point. Our results help
to assess the validity of empirical studies that take the status quo as the reference point.
We tested the reference point rules in a lab experiment with large incentives
(subjects could win up to a weekly salary) and used a Bayesian hierarchical approach to
analyze the data. Bayesian analysis strikes a nice balance between pooling and
individual estimation and it leads to more precise parameter estimates. A potential
limitation of Bayesian analysis is that the selected priors can affect the estimations, but
in our analysis the choice of priors had negligible impact on the estimates.
29
To make inferences about the different reference point rules, we used a
comprehensive model which allowed isolating the impact of the reference point rule
from the other behavioral parameters. This approach is cleaner and better interpretable
than the common practice in mixture modeling where each model in the mixture is
specified separately and parameterizations can differ across models and also than horse
races between models based on criteria like the Akaike Information Criterion. Using a
Bayesian model has the additional advantage that we could obtain the parameter
estimates for both the distribution of reference point rules in the population and each
subject separately.
Our robustness tests have two interesting implications for the modeling of
reference-dependent preferences. First, they indicate that models with a choice-specific
reference point do not benefit from including consumption utility. Kahneman and
Tversky (1979, p.277) argue that even though an individual’s attitudes to money
depend both on his asset position and on changes from his reference point, a utility
function that is only defined over changes from the reference point generally provides a
satisfactory approximation. Our results provide support for their argument.
Second, we concluded that probability weighting played an important role and could
not be ignored. The fit of expectation-based prospect-specific models like Köszegi and
Rabin’s (2006, 2007) model, which in their original form do not assume probability
weighting, clearly improved when probability weighting was included. A complication
in these model is how the reference point is determined when decision makers weight
probabilities.
Our analysis assumed that subjects consider each choice in isolation from the other
choices and from the one third chance that they would be selected to play out one of
their choices for real. This assumption is common in experimental economics and there
30

exists support for it (Starmer and Sugden 1991, Cubitt et al. 1998, Bardsley et al.
2010).
14
If some subjects did not isolate choices, but instead viewed the experiment as a
compound lottery, then this would create additional support for the status quo as
Maxmin and MaxP subjects would then also use the status quo as their reference point.
An interesting question to explore is whether our results can be generalized to other
decision contexts than the one we considered. For example our experiment involved
discrete distributions whereas in economic contexts continuous distributions are often
relevant. Also, the minimum probability that we included was 5% whereas real-world
decisions frequently involve smaller probabilities, e.g. the annual risk of contracting a
fatal disease. It is, for instance, unclear whether MaxMin would perform as well if the
lowest outcome occurred with only a very small probability.
We did not test all reference points that have been proposed in the literature. As we
explained in the introduction, we followed Rabin’s (2013) approach and studied
reference point rules that used the same independent variables as the core economic
theory of decision under risk, expected utility. This implied, for example, that we did not
test explicitly for subjects’ goals or aspirations as these require other inputs based on
introspection. On the other hand, subjects may have had few goals or aspirations for the
current experiment and it is also possible that their goals were equal to one of the
reference points that we used (e.g. expected value or the security level). We also did not
test reference point rules that would be based on previous choices. Such rules would
introduce new degrees of freedom (which piece of information from these choices,
number of past choices remembered, aggregation/updating rule…). Our cross-
validation exercise indicated that the rules that we included captured our subjects’
14
Cox et al. (2015) found evidence against isolation.
31
preferences accurately and that the model was not misspecified due to the omission of
reference point rules.
8. Conclusion
Reference-dependence is a key concept in explaining people’s choices, but little insights
exists into the question how reference points are formed. Reference-dependent theories
give no guidance about this question. This paper has estimated the prevalence of six
reference point rules using a unique data set in which we used stakes up to a weekly
salary. We modeled the reference point rule as a latent categorical variable, which we
estimated using Bayesian hierarchical modeling. Our results indicate that the status quo
and MaxMin are the most commonly used reference points. Around twenty percent of
the subjects used an expectations-based reference point.
32

Appendix A: The experimental questions and the predicted reference points.
Table A1 describes the 70 choices of the experiments, between prospects =
(
,
;
,
;
,
; 1
,
)
and =
(
,
;
,
;
,
; 1
,
)
. The last five columns give the choice-specific reference points of the MaxMin, MinMax and X at
Max P rules, and the prospect-specific reference points of the Expected Value rule. The reference point of the Satus Quo rule is always 0
and the prospect-specific reference points of the sixth and last rule were and themselves.
#
MaxMin
MinMax
X at Max P
Expected Value
1
267
313
453
546
0.1
0.8
0.05
127
220
406
0.15
0.05
0.8
267
406
313
327.05
354.85
2
159
221
408
0.7
0.1
0.2
34
97
346
0.1
0.3
0.6
159
346
159
215
240.1
3
183
233
384
485
0.7
0.05
0.1
32
132
334
0.15
0.05
0.8
183
334
334
250.9
278.6
4
223
263
383
0.4
0.5
0.1
143
183
343
0.1
0.4
0.5
223
343
263
259
259
5
127
255
287
0.7
0.05
0.25
95
191
223
0.15
0.05
0.8
127
223
223
173.4
202.2
6
103
213
377
0.6
0.15
0.25
48
158
267
322
0.3
0.1
0.05
103
322
103
188
220.65
7
92
245
0.85
0.15
16
130
206
0.1
0.7
0.2
92
206
92
114.95
133.8
8
135
290
329
0.55
0.35
0.1
96
213
251
0.25
0.05
0.7
135
251
251
208.65
210.35
9
209
309
459
0.35
0.55
0.1
159
259
359
409
0.05
0.55
0.1
209
409
309
289
309
10
221
504
0.85
0.15
80
292
434
0.05
0.7
0.25
221
434
221
263.45
316.9
11
64
188
313
0.4
0.1
0.5
2
126
251
375
0.25
0.4
0.1
64
313
313
200.9
169.75
12
122
270
418
0.15
0.8
0.05
48
196
344
492
0.1
0.35
0.45
122
418
270
255.2
277.4
13
224
416
0.55
0.45
95
352
480
0.25
0.7
0.05
224
416
352
310.4
294.15
14
100
211
0.2
0.8
64
137
285
0.2
0.5
0.3
100
211
211
188.8
166.8
15
257
427
0.8
0.2
143
370
484
0.35
0.45
0.2
257
427
257
291
313.35
16
223
416
0.45
0.55
159
287
544
0.05
0.7
0.25
223
416
287
329.15
344.85
17
219
448
0.2
0.8
143
296
372
601
0.1
0.1
0.7
219
448
448
402.2
364.4
18
99
225
0.8
0.2
16
141
183
266
0.1
0.4
0.45
99
225
99
124.2
153.65
19
94
187
0.3
0.7
64
125
156
248
0.25
0.3
0.05
94
187
187
159.1
160.5
33

20
203
317
0.75
0.25
127
241
279
354
0.35
0.05
0.45
203
317
203
231.5
235.15
21
138
245
0.55
0.45
30
84
191
352
0.05
0.05
0.85
138
245
191
186.15
185.65
22
118
200
0.8
0.2
64
91
173
228
0.2
0.1
0.6
118
200
118
134.4
148.5
23
232
374
0.4
0.6
91
161
303
515
0.05
0.1
0.6
232
374
374
317.2
331.2
24
233
344
0.7
0.3
159
196
307
381
0.3
0.2
0.1
233
344
233
266.3
270
25
251
358
0.7
0.3
143
304
412
465
0.05
0.85
0.05
251
358
304
283.1
309.4
26
105
278
0.25
0.75
48
163
336
394
0.25
0.4
0.1
105
278
278
234.75
209.3
27
183
302
0.6
0.4
64
242
361
421
0.15
0.7
0.1
183
302
242
230.6
236.15
28
61
179
0.45
0.55
22
101
218
257
0.4
0.05
0.5
61
179
179
125.9
135.7
29
147
367
0.6
0.4
0
74
367
0.25
0.05
0.7
147
367
367
235
260.6
30
99
251
0.6
0.4
48
251
0.4
0.6
99
251
99
159.8
169.8
31
259
558
0.75
0.25
159
359
558
0.15
0.7
0.15
259
558
259
333.75
358.85
32
168
397
0.6
0.4
16
92
397
0.05
0.4
0.55
168
397
168
259.6
255.95
33
209
407
0.75
0.25
143
407
0.5
0.5
209
407
209
258.5
275
34
120
243
0.75
0.25
80
161
243
0.15
0.7
0.15
120
243
120
150.75
161.15
35
142
209
277
0.7
0.05
0.25
74
108
277
0.4
0.1
0.5
142
277
142
179.1
178.9
36
151
230
348
0.5
0.15
0.35
111
269
348
0.25
0.6
0.15
151
348
269
231.8
241.35
37
140
200
261
0.85
0.05
0.1
80
110
261
0.05
0.55
0.4
140
261
140
155.1
168.9
38
79
170
308
0.25
0.7
0.05
33
216
308
0.15
0.8
0.05
79
308
216
154.15
193.15
39
192
341
0.15
0.85
192
390
439
0.55
0.4
0.05
192
341
341
318.65
283.55
40
15
290
0.3
0.7
15
382
0.5
0.5
15
290
290
207.5
198.5
41
95
443
0.3
0.7
95
327
559
0.1
0.8
0.1
95
443
327
338.6
327
42
102
311
0.15
0.85
102
381
450
0.55
0.25
0.2
102
311
311
279.65
241.35
43
127
284
0.2
0.8
127
336
0.45
0.55
127
284
284
252.6
241.95
44
54
259
0.3
0.7
54
191
328
0.05
0.85
0.1
54
259
191
197.5
197.85
45
127
259
390
0.05
0.4
0.55
127
456
521
0.45
0.15
0.4
127
390
390
324.45
333.95
46
57
221
331
0.3
0.1
0.6
57
167
386
0.1
0.6
0.3
57
331
331
237.8
221.7
47
111
194
277
0.1
0.05
0.85
111
318
359
0.5
0.3
0.2
111
277
277
256.25
222.7
48
6
229
377
0.05
0.8
0.15
6
155
451
0.1
0.7
0.2
6
377
229
240.05
199.3
49
100
1
13
186
0.45
0.55
100
100
100
100
108.15
34

50
224
1
12
294
0.25
0.75
224
224
224
224
223.5
51
276
1
80
374
472
0.35
0.45
0.2
276
276
276
276
290.7
52
203
1
106
154
299
0.45
0.05
0.5
203
203
203
203
204.9
53
196
1
95
146
246
297
0.3
0.05
0.5
196
196
196
196
203.35
54
383
1
171
453
0.25
0.75
383
383
383
383
382.5
55
297
404
0.55
0.45
189
243
350
511
0.05
0.05
0.85
297
404
350
345.15
344.65
56
220
338
0.45
0.55
181
260
377
416
0.4
0.05
0.5
220
338
338
284.9
294.7
57
238
329
467
0.25
0.7
0.05
192
375
467
0.15
0.8
0.05
238
467
375
313.15
352.15
58
301
368
436
0.7
0.05
0.25
233
267
436
0.4
0.1
0.5
301
436
301
338.1
337.9
59
259
1
172
345
0.45
0.55
259
259
259
259
267.15
60
362
1
265
313
458
0.45
0.05
0.5
362
362
362
362
363.9
61
213
418
0.3
0.7
213
350
487
0.05
0.85
0.1
213
418
350
356.5
356.85
62
223
347
472
0.4
0.1
0.5
161
285
410
534
0.25
0.4
0.1
223
472
472
359.9
328.75
63
306
526
0.6
0.4
159
233
526
0.25
0.05
0.7
306
526
526
394
419.6
64
251
358
0.7
0.3
143
304
412
465
0.05
0.85
0.05
251
358
304
283.1
309.4
65
95
443
0.3
0.7
95
327
559
0.1
0.8
0.1
95
443
327
338.6
327
66
223
416
0.45
0.55
159
287
544
0.05
0.7
0.25
223
416
287
329.15
344.85
67
209
407
0.75
0.25
143
407
0.5
0.5
209
407
209
258.5
275
68
138
245
0.55
0.45
30
84
191
352
0.05
0.05
0.85
138
245
191
186.15
185.65
69
111
207
223
0.5
0.4
0.1
80
95
207
0.1
0.4
0.5
111
207
111
160.6
149.5
70
111
175
207
0.1
0.4
0.5
80
159
191
0.25
0.25
0.5
111
191
207
184.6
155.25
Table A1. Choices and reference points
35
Appendix B: The procedure to construct the experimental choices
The selection of experimental questions was guided by the following contrasting
principles:
- Questions must be diverse in terms of number of outcomes and magnitudes of
probabilities involved.
- Questions within each choice must have non-matching maximal or minimal
outcomes.
- Questions must be diverse in terms of relative positioning in the outcome space
(a.k.a. shifting; see the description below).
- Questions must have similar expected value to avoid trivial or statistically non-
informative choice situations.
- Question pairs must be "orthogonal" in some sense in order to maximize statistical
efficiency.
Our question set (Table A1) consists of six homogeneous groups which are illustrated
graphically in Figure B1. The first group is a set of 8 questions where one of the
prospects is certainty and the other option is a two to four outcome prospect (Figure
B1a). The second set consists of two choice situations where one prospect stochastically
dominates the other (Figure B1b). The third set comprises 10 choices where one
prospect is relatively shifted - both minimum and maximum are relatively higher than
for the other prospect (Figure B1c). The fourth group consists of 12 questions for which
minimum outcome coincides (Figure B1d). The fifth group consists of 14 questions for
which the maximum outcome coincides (Figure B1e). The last three groups (Figure B1f-
h) consists of 24 questions where the range of one prospect is within the range of the
other prospect. This group is further split into three homogeneous sub-groups
determined by number of outcomes in the smaller prospect (2 vs 3) and by the amount
36

of shift of the smaller prospect with respect to the bigger one (1 or 2 outcomes). Choices
in all groups are roughly balanced with respect to the relative shift (there are both one-
and two-outcome shifted questions on the either side of the prospects).
In order to maximize statistical efficiency and minimize redundancy, within each group
of questions we perform the exhaustive search that minimizes the sum of the pairwise
cross-choice covariance within that group. We defined the cross-choice covariance for a
choice pair (1, 2), (2, 2) as (
((,) (,))
)
. This is an intuitive counterpart
of the statistical co-variance. For each sub-group of choices, we optimized the sum of all
pairwise cross-choice co-variances within that group.
37
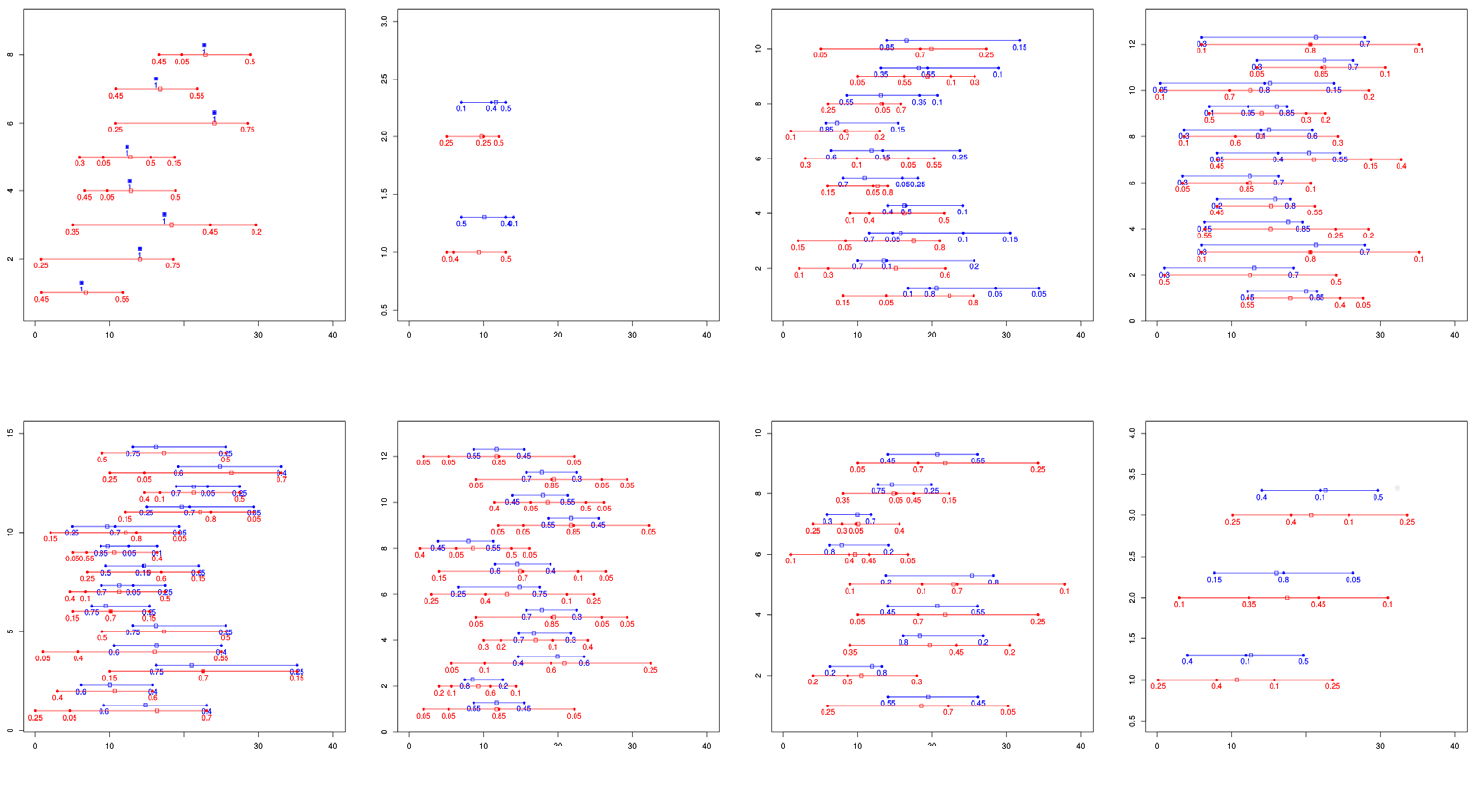
Figure B1: Choices used in the experiment.
Each sub-figure represents a group of homogeneous choices. Each question consists of two prospects (blue and red). X axis represents
the amounts in euro and Y axis has no quantitative meaning. Numbers below the prospect lines are the outcome probabilities. Small
squares are the expectations of the prospects. (a) group with certainty equivalents, (b) stochastic dominance group, (c) shifted group
(extremes of blue prospect are shifted with respect to the red prospect), (d) minima of blue and red prospects coincide, (e) maxima of
red and blue prospects coincide, (f-h) three groups for which the range of the blue object is inside the range of the red prospect.
(a)
(b)
(c)
(d)
(e)
(f)
(g)
(h)
38
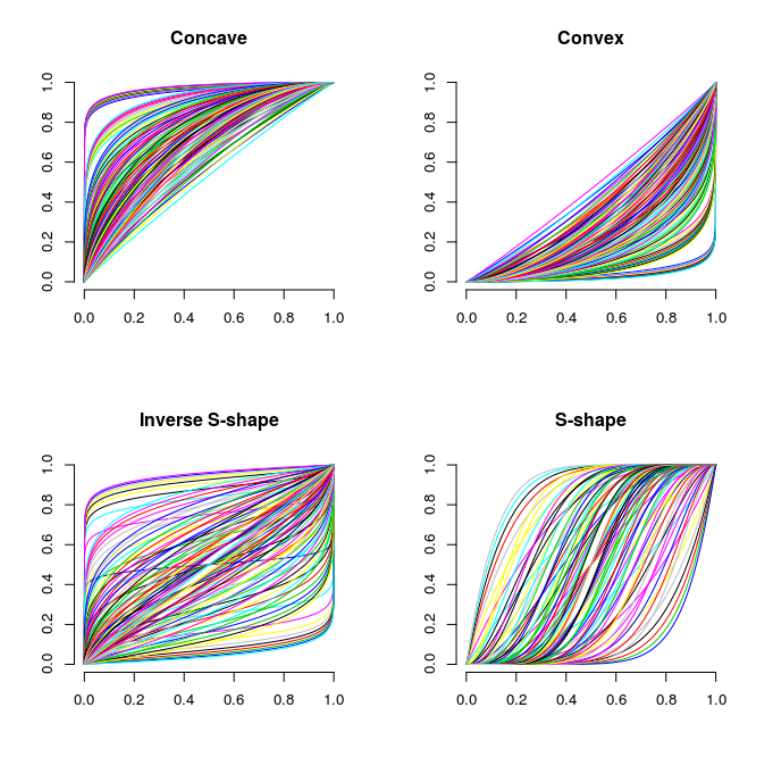
Appendix C: IBeta
The incomplete regularized beta function (), is a very flexible monotonically
increasing
[
0,1
]
[0,1] function. It can capture a wide range of convex, concave, S-
shape and inverse S-shape functions without favoring specific shapes or inflection
points. The family is symmetric in the sense that (; , ) = 1 (1
; , ). Various shapes of function are illustrated in Figure C.1.
Figure C.1. Various shapes of the function
40
References
Abdellaoui M (2000) Parameter-free elicitation of utility and probability weighting functions.
Management Science 46: 1497-1512.
Abeler J, Falk, A, Goette, L, Huffman, D (2011) Reference points and effort provision. The
American Economic Review 101: 470-492.
Allen EJ, Dechow, PM, Pope, DG, Wu, G (forthcoming) Reference-dependent preferences:
Evidence from marathon runners. Management Science .
Barber BM, Odean, T (2008) All that glitters: The effect of attention and news on the buying
behavior of individual and institutional investors. Review of Financial Studies 21: 785-
818.
Barberis NC (2013) Thirty years of prospect theory in economics: A review and assessment.
Journal of Economic Perspectives 27: 173-196.
Bardsley N, Cubitt, R, Loomes, G, Moffatt, P, Starmer, C, Sugden, R (2010) Experimental
economics: Rethinking the rules (Princeton University Press, Princeton and Oxford).
Bartling B, Brandes, L, Schunk, D (2015) Expectations as reference points: Field evidence
from professional soccer. Management Science 61: 2646-2661.
Baucells M, Weber, M, Welfens, F (2011) Reference-point formation and updating.
Management Science 57: 506-519.
Bell DE (1985) Disappointment in decision making under uncertainty. Operations Research
33: 1-27.
Benartzi S, Previtero, A, Thaler, RH (2011) Annuitization puzzles. The Journal of Economic
Perspectives 25: 143-164.
Benartzi S, Thaler, RH (1995) Myopic loss aversion and the equity premium puzzle.
Quarterly Journal of Economics 110: 73-92.
Birnbaum MH, Schmidt, U (2010) Testing transitivity in choice under risk. Theory and
Decision 69: 599-614.
Bleichrodt H, Schmidt, U (2005) Context- and reference-dependent utility: A generalization
of prospect theory. Working Paper.
Bleichrodt H, Pinto, JL (2000) A parameter-free elicitation of the probability weighting
function in medical decision analysis. Management Science 46: 1485-1496.
Bleichrodt H, Pinto, JL, Wakker, PP (2001) Making descriptive use of prospect theory to
improve the prescriptive use of expected utility. Management Science 47: 1498-1514.
41
Bordalo P, Gennaioli, N, Shleifer, A (2012) Salience theory of choice under risk. The
Quarterly Journal of Economics 127: 1243-1285.
Card D, Dahl, GB (2011) Family violence and football: The effect of unexpected emotional
cues on violent behavior. Quarterly Journal of Economics 126: 103-143.
Chetty R, Looney, A, Kroft, K (2009) Salience and taxation: Theory and evidence. The
American Economic Review 99: 1145-1177.
Chew SH, Epstein, LG, Segal, U (1991) Mixture symmetry and quadratic utility.
Econometrica 139-163.
Chew SH, Epstein, LG, Segal, U (1994) The projective independence axiom. Economic
Theory 4: 189-215.
Cox JC, Sadiraj, V, Schmidt, U (2015) Paradoxes and mechanisms for choice under risk.
Experimental Economics 18: 215-250.
Crawford VP, Meng, J (2011) New york city cab drivers' labor supply revisited: Reference-
dependent preferences with rational expectations targets for hours and income. American
Economic Review 101: 1912-1932.
Cubitt R, Starmer, C, Sugden, R (1998) On the validity of the random lottery incentive
system. Experimental Economics 1: 115-131.
Delquié P, Cillo, A (2006) Disappointment without prior expectation: A unifying perspective
on decision under risk. Journal of Risk and Uncertainty 33: 197-215.
Diecidue E, Van de Ven, J (2008) Aspiration level, probability of success and failure, and
expected utility. International Economic Review 49: 683-700.
Eil D, Lien, JW (2014) Staying ahead and getting even: Risk attitudes of experienced poker
players. Games and Economic Behavior 87: 50-69.
Fox CR, Poldrack, RA (2014) Prospect theory and the brain. Glimcher Paul, Fehr Ernst, eds.
Handbook of Neuroeconomics (2nd Ed.) (Elsevier, New York), 533-567.
Gelfand AE, Smith, AF (1990) Sampling-based approaches to calculating marginal densities.
Journal of the American Statistical Association 85: 398-409.
Genesove D, Mayer, CJ (2001) Loss aversion and seller behavior: Evidence from the housing
market. Quarterly Journal of Economics 116: 1233-1260.
Gill D, Prowse, V (2012) A structural analysis of disappointment aversion in a real effort
competition. The American Economic Review 102: 469-503.
Gonzalez R, Wu, G (1999) On the form of the probability weighting function. Cognitive
Psychology 38: 129-166.
Gul F (1991) A theory of disappointment aversion. Econometrica 59: 667-686.
42
Heath C, Larrick, RP, Wu, G (1999) Goals as reference points. Cognitive Psychology 38: 79-
109.
Heidhues P, Kőszegi, B (2008) Competition and price variation when consumers are loss
averse. The American Economic Review 1245-1268.
Hershey JC, Schoemaker, PJH (1985) Probability versus certainty equivalence methods in
utility measurement: Are they equivalent? Management Science 31: 1213-1231.
Johnson EJ, Goldstein, D (2003) Do defaults save lives? Science 302: 1338-1339.
Kahneman D, Tversky, A (1979) Prospect theory: An analysis of decision under risk.
Econometrica 47: 263-291.
Köszegi B, Rabin, M (2007) Reference-dependent risk attitudes. The American Economic
Review 97: 1047-1073.
Köszegi B, Rabin, M (2006) A model of reference-dependent preferences. Quarterly Journal
of Economics 121: 1133-1166.
Lien JW, Zheng, J (2015) Deciding when to quit: Reference-dependence over slot machine
outcomes. American Economic Review: Papers & Proceedings 105: 366-370.
Loomes G, Sugden, R (1986) Disappointment and dynamic consistency in choice under
uncertainty. Review of Economic Studies 53: 271-282.
Luce RD (1959) On the possible psychophysical laws. Psychological Review 66: 81.
Machina M (1982) 'Expected utility' analysis without the independence axiom. Econometrica
50: 277-323.
Masatlioglu Y, Raymond, C (2016) A behavioral analysis of stochastic reference dependence.
American Economic Review 106: 2760-2782.
Meng, J. Weing, X. (forthcoming). Can prospect theory expain the disposition effect? A new
perspective on reference points. Management Science.
Nilsson H, Rieskamp, J, Wagenmakers, E (2011) Hierarchical bayesian parameter estimation
for cumulative prospect theory. Journal of Mathematical Psychology 55: 84-93.
Odean T (1998) Are investors reluctant to realize their losses? Journal of Finance 53: 1775-
1798.
Pope DG, Schweitzer, ME (2011) Is tiger woods loss averse? persistent bias in the face of
experience, competition, and high stakes. The American Economic Review 101: 129-157.
Prelec D (1998) The probability weighting function. Econometrica 66: 497-528.
Quiggin J (1981) Risk perception and risk aversion among australian farmers. Australian
Journal of Agricultural Economics 25: 160-169.
43
Quiggin J (1982) A theory of anticipated utility. Journal of Economic Behavior and
Organization 3: 323-343.
Rabin M (2013) An approach to incorporating psychology into economics. The American
Economic Review 103: 617-622.
Rabin M (2000) Risk aversion and expected-utility theory: A calibration theorem.
Econometrica 68: 1281-1292.
Rosato A, Tymula, A (2016) Loss aversion and competition in vickrey auctions: Money ain't
no good.
Rouder JN, Lu, J (2005) An introduction to bayesian hierarchical models with an application
in the theory of signal detection. Psychonomic Bulletin & Review 12: 573-604.
Samuelson W, Zeckhauser, R (1988) Status quo bias in decision making. Journal of Risk and
Uncertainty 1: 7-59.
Schmidt U, Starmer, C, Sugden, R (2008) Third-generation prospect theory. Journal of Risk
and Uncertainty 36: 203-223.
Schneider M, Day, R (forthcoming) Target-adjusted utility functions and expected-utility
paradoxes. Management Science .
Starmer C, Sugden, R (1991) Does the random-lottery incentive system elicit true
preferences? an experimental investigation. American Economic Review 81: 971-978.
Stott HP (2006) Cumulative prospect theory's functional menagerie. Journal of Risk and
Uncertainty 32: 101-130.
Sugden R (2003) Reference-dependent subjective expected utility. Journal of Economic
Theory 111: 172-191.
Sydnor J (2010) (Over) insuring modest risks. American Economic Journal: Applied
Economics 2: 177-199.
Thaler RH, Benartzi, S (2004) Save more tomorrow™: Using behavioral economics to
increase employee saving. Journal of Political Economy 112: S164-S187.
Toubia O, Johnson, E, Evgeniou, T, Delquié, P (2013) Dynamic experiments for estimating
preferences: An adaptive method of eliciting time and risk parameters. Management
Science 59: 613-640.
Tversky A, Kahneman, D (1992) Advances in prospect theory: Cumulative representation of
uncertainty. Journal of Risk and Uncertainty 5: 297-323.
Van Osch S, Stiggelbout, AM (2008) The construction of standard gamble utilities. Health
Economics 17: 31-40.
44
van Osch S,M.C., van den Hout, WB, Stiggelbout, AM (2006) Exploring the reference point
in prospect theory: Gambles for length of life. Medical Decision Making 26: 338-346.
van Osch SMC, Wakker, PP, van den Hout, WB, Stiggelbout, AM (2004) Correcting biases
in standard gamble and time tradeoff utilities. Medical Decision Making 24: 511-517.
Wilcox, N. T. 2012. Plenary lecture FUR atlanta.
Wu G, Gonzalez, R (1996) Curvature of the probability weighting function. Management
Science 42: 1676-1690.
45
