
One-to-One and
Inverse Functions
2.3
Introduction
In this Section we examine more terminology associated with functions. We explain one-to-one and
many-to-one functions and show how the rule associated with certain functions can be reversed to
give so-called inverse functions. These ideas will be needed when we deal with particular functions
in later Sections.
Prerequisites
Before starting this Section you should . . .
• understand what is meant by a function
• be able to sketch graphs of simple functions
'
&
$
%
Learning Outcomes
On completion you should be able to . . .
• explain what is meant by a one-to-one
function
• explain what is meant by a many-to-one
function
• explain what is meant by an inverse function,
and determine when and how such a function
can be found
20 HELM (2008):
Workbook 2: Basic Functions
®
1. One-to-many rules, many-to-one and one-to-one
functions
One-to-many rules
Recall from Section 2.1 that a rule for a function must produce a single output for a given inp ut.
Not all rules satisfy this criterion. For example, the rule ‘take the square root of the input’ cannot be
a rule for a function because for a given input there are two outputs; an input of 4 produces outputs
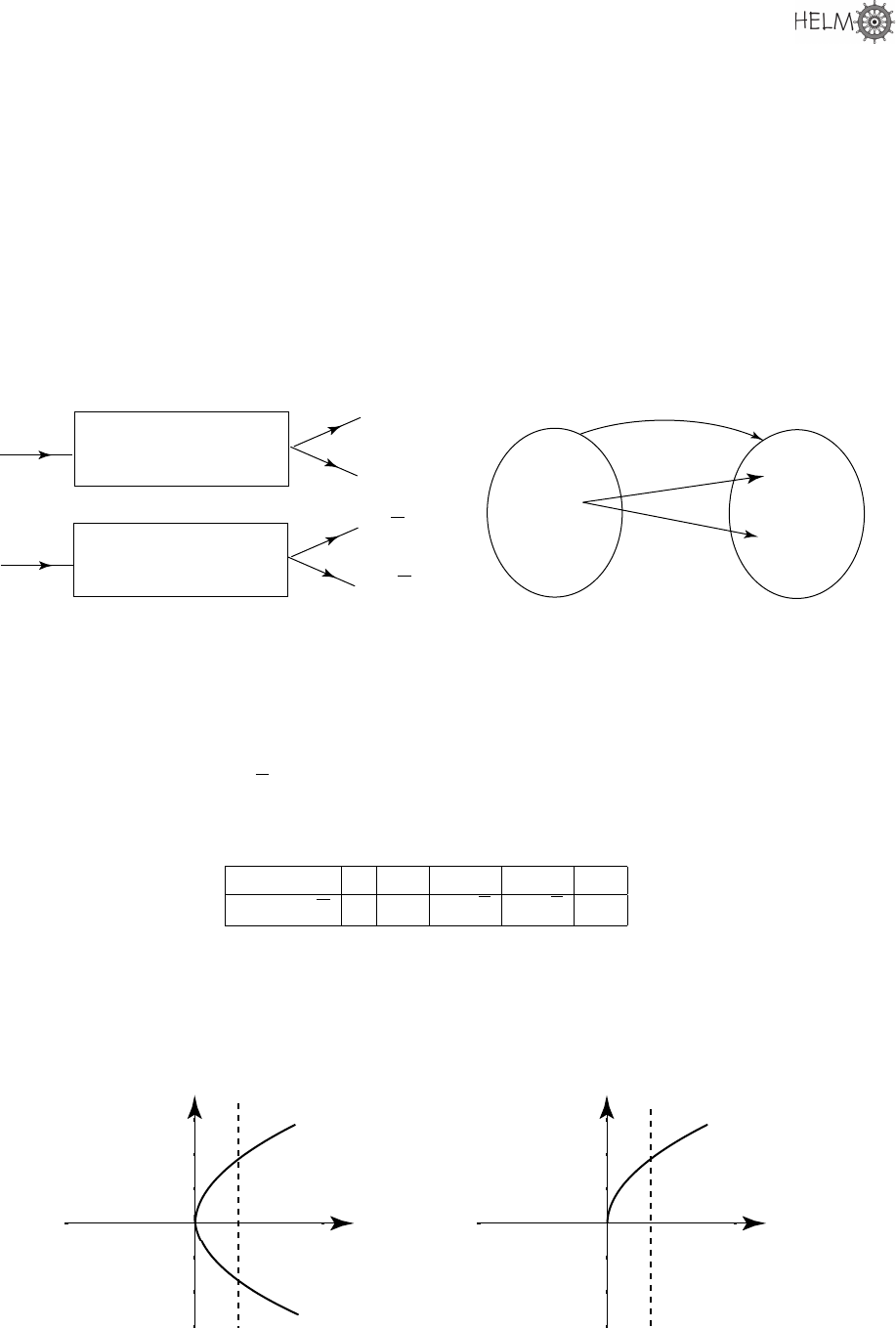
of 2 and −2. Figure 10 shows two ways in which we can picture this situation, the first being a b lock
diagram, and the second using two sets representing input and output values and the relationship
between them.
x
√
x
−
√
x
take the square root
of the input
input
output
−2
2
4
take the square root
of the input
−2
2
4
t
a
k
e
t
h
e
s
q
u
a
r
e
r
o
o
t
Figure 10: This rule cannot be a function - it is a one-to-many rule
Such a rule is described as a one-to-many rule. This means that one i npu t produces more than
one output. This is obvious from inspecting the sets in Figure 10.
The graph of the rule ‘take ±
√
x’ can be drawn by constructing a table of values:
Table 4
x 0 1 2 3 4
y = ±
√
x 0 ±1 ±
√
2 ±
√
3 ±2
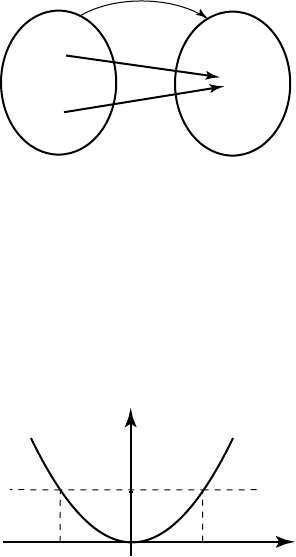
The graph is shown in Figure 11(a). For each value of x there are two corresponding values of y.
Plotting a graph of a one-to-many rule will result in a curve through which a vertical line can be
drawn which cuts the curve more than once as you can see. The vertical line cuts the curve more
than once because there is m ore than one y value for each x value.
x
y
x
y
(a)
(b)
Figure 11
HELM (2008):
Section 2.3: One-to-One and Inverse Functions
21
By describing a rule more carefully it is possible to make sure a single output results from a single
input, thereby defining a valid rule for a function. For example, the rule ‘take the positive square
root of the input’ is a valid function rule because a given input produces a single output. The graph
of this function is displayed in Figure 11(b).
Many-to-one and one-to-one functions
Consider the function y(x) = x
2
. An input of x = 3 produces an output of 9. Similarly, an i npu t of
−3 also produces an output of 9. In general, a function for which different inputs can produce the
same output is called a many-to-one function. This is represented pictorially in Figure 12 from
which it is clear why we call this a many-to-one function.
input
output
−3
3
9
y = x
2
Figure 12: This represents a many-to-one function
Note that whilst this is many-to-one it is still a function since any chosen input value has only one
arrow emerging from it. Thus there is a single output for each input.
It is possible to decide if a function is many-to-one by examining its graph. Consider the graph of
y = x
2
shown in Figure 13.
−3
3
y = x
2
y
x
9
Figure 13: The function y = x
2
is a many-to-one function
We see that a horizontal line drawn on the graph cuts it more than once. This means that two (or
more) different inputs have yielded the same output and s o the function is many-to-one.
If a function is not many-to-one then it is said to be one-to-one. This means that each different
input to the function yields a different output.
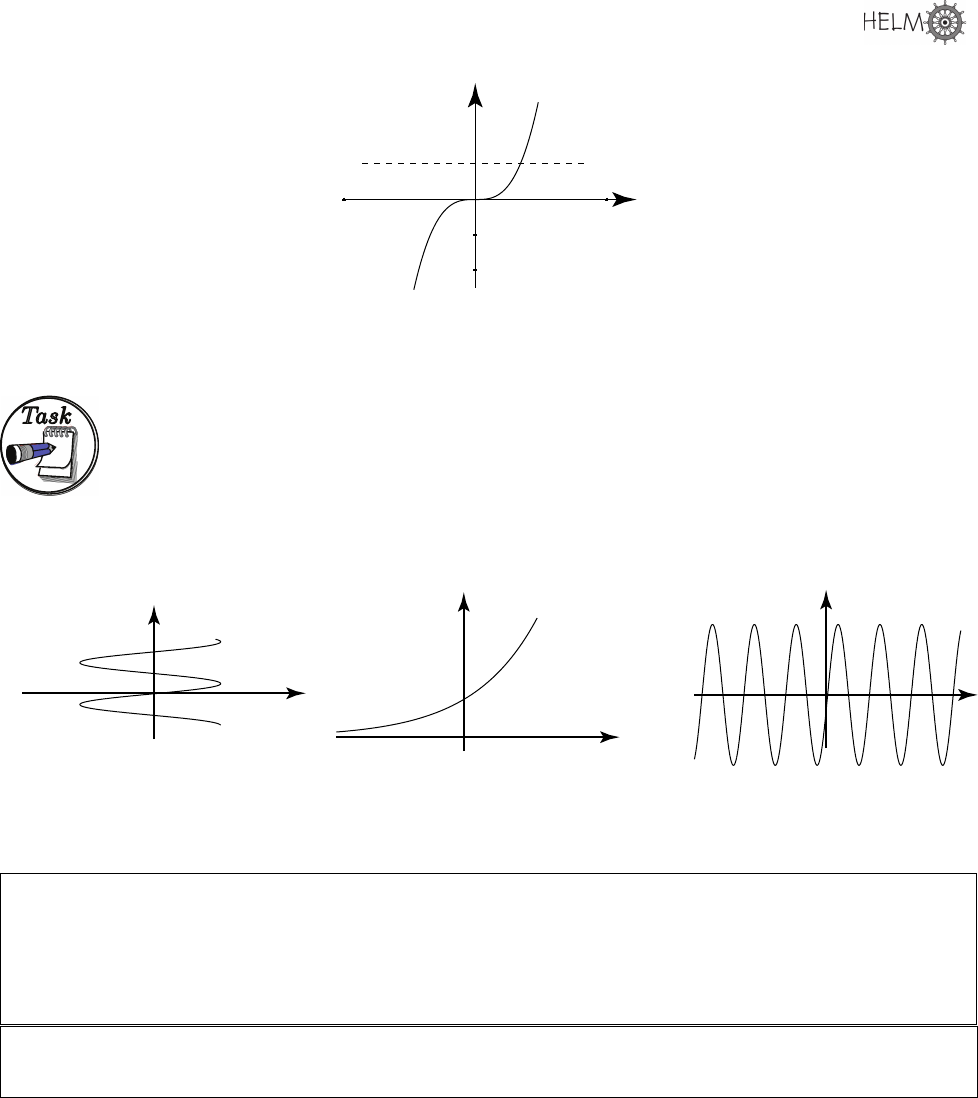
Consider the function y(x) = x
3
which is shown in Figure 14. A horizontal line drawn on this graph
will intersect the curve only once. This means that each input value of x yields a different output
value for y.
22 HELM (2008):
Workbook 2: Basic Functions
®
= x
3
y
y
x
−10
− 5
5
10
Figure 14: The function y(x) = x
3
is a one-to-one function
Task
Study the graphs shown in Figure 15. Decide which, if any, are graphs of functions.
For those which are, state if the function is one-to-one or many-to-one.
a) b) c)
y
x
y
x
y
x
Figure 15
Your solution
Answer
(a) not a function, (b) one-to-one function, (c) many-to-one function
2. Inverse of a function
We have seen that a function can be regarded as taking an input, x, and processing it in some way
to produce a single output f (x) as shown in Figure 16(a). A natural question to ask is whether we
can find another function that will reverse the proces s. In other words, can we find a function that
will start with f(x) and process it to produce x again? This idea is also shown in Figure 16(b). If we
can find such a function it is called the inverse function to f (x) and is given the symbol f
−1
(x).
Do not confuse the ‘−1’ with an index, or power. Here the superscript is used purely as the notation
for the inverse function. Note that the composi te function f
−1
(f(x)) = x as shown in Figure 17.
HELM (2008):
Section 2.3: One-to-One and Inverse Functions
23
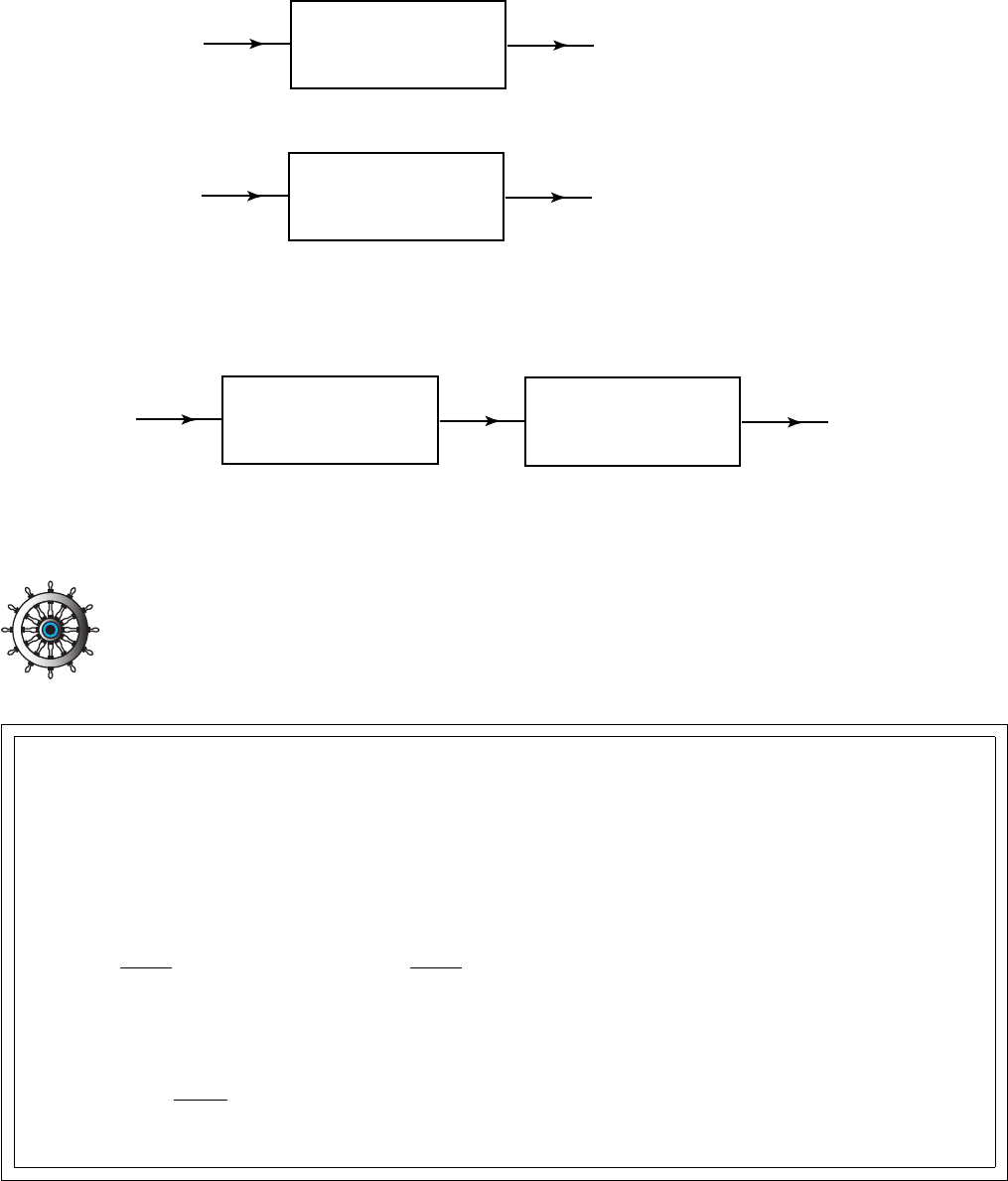
process
reverse process
f
f
−1
x
f(x)
f(x)
x
(a)
(b)
Figure 16: The second block reverse the process in the first
process
reverse process
f
f
−1
x
f(x)
x
Figure 17: f
−1
reverses the process in f
Example 6
Find the inverse function to f (x) = 3x − 8.
Solution
The given function takes an input, x and produces an output 3x − 8. The inverse function, f
−1
,
must take an input 3x − 8 and give an output x. That is
f
−1
(3x − 8) = x
If we introduce a new variable z = 3x − 8, and transpose this for x to give
x =
z + 8
3
then f
−1
(z) =
z + 8
3
So the rule for f
−1
is add 8 to the input and divide the result by 3. Writing f
−1
with x as its
argument gives
f
−1
(x) =
x + 8
3
This is the inverse function.
24 HELM (2008):
Workbook 2: Basic Functions
®
Not all functions possess an inverse function. In fact, only one-to-one functions do so. If a function
is many-to-one the process to reverse it would require many outputs from one input contradicting
the definition of a function.
Task
Find the inverse of the function f (x) = 7 − 3x, using the fact that the inverse
function must take an input 7−3x and produce an output x. So f
−1
(7−3x) = x
Introduce a new variable z so that z = 7 − 3x and transpose this to find x. Henc e write down the
inverse function:
Your solution
Answer
f
−1
(z) =
7 − z
3
. With x as its argument the inverse function is f
−1
(x) =
7 − x
3
.
Exercises
1. Explain why a one-to-many rule cannot be a function.
2. Illustrate why y = x
4
is a many-to-one function by providing a suitable example.
3. By sketching a graph of y = 3x − 1 show that this is a one-to-one function.
4. Explain why a many-to-one function does not have an inverse function. Give an example.
5. Find the inverse of each of the following functions:
(a) f (x) = 4x + 7, (b) f (x) = x, (c) f (x) = −23x, (d) f (x) =
1
x + 1
.
Answers
5. (a) f
−1
(x) =
x − 7
4
, (b) f
−1
(x) = x, (c) f
−1
(x) = −
x
23
, (d) f
−1
(x) =
1 − x
x
.
HELM (2008):
Section 2.3: One-to-One and Inverse Functions
25
