
HAL Id: hal-00783048
https://inria.hal.science/hal-00783048
Submitted on 31 Jan 2013
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
The Dynamic Dictionary of Mathematical Functions
(DDMF)
Alexandre Benoit, Frédéric Chyzak, Alexis Darrasse, Stefan Gerhold, Marc
Mezzarobba, Bruno Salvy
To cite this version:
Alexandre Benoit, Frédéric Chyzak, Alexis Darrasse, Stefan Gerhold, Marc Mezzarobba, et al.. The
Dynamic Dictionary of Mathematical Functions (DDMF). ICMS 2010 - Third International Congress
on Mathematical Software, Sep 2010, Kobe, Japan. pp.35-41. �hal-00783048�

The Dynamic Dictionary of
Mathematical Functions (DDMF)
⋆
Alexandre Benoit, Fr´ed´eric Chyzak, Alexis Darrasse, Stefan Gerhold,
Marc Mezzarobba, and Bruno Salvy
Inria Paris-Rocquencourt, France
http://ddmf.msr-inria.inria.fr
Abstract. We describe the main features of the Dynamic Dictionary
of M a t h emat i ca l Functions (version 1. 5) . It is a website consist in g of
interactive tables of mathematical formulas on elementary and special
functions. The formulas are automatically generated by computer algebra
routines. The user can ask for more terms of the expansions, more digits
of the numerical values, or proofs of some of the formulas.
1 Motivation
Dictionaries of mathematical functions are com mon ly used by scientists and
engineers. Some of the most famous ones are Abramowitz & Stegun’s Hand-
book of Mathematical Functions [1]; the Bateman pr oject Higher Transcenden-
tal Functions [7]; Gradshtein & Ryzhik’s Table of Integrals, Series, and Prod-
ucts [8]; and the multivolume Integrals and Series by Prudnikov, Brychkov, and
Marichev [15]. T he se dictionaries gather formulas such as differential equati on s,
definite and indefinite integrals, inequaliti e s, recurrence relations, power series,
asymptotic expansions, approximations, and sometimes graphs and numerical
tables, for a large set of functions. They have b e en prepared by specialists of
these functions and carefully checked and proofread. Their success is attested to
by the hundreds of thousands of citations they have received [3].
The first editions of those books were published between 60 and 30 years ago.
Since then, the advent of the World Wide Web has changed th e way people
now look for information. Aware of t hi s change, the NIST has pu bl i sh ed a new
version of [1] in 2010, called the NIST Handbook of Mathematical Functions [13]
together with a web site, the NIST Digital Library of Mathematical Functions.
This site offers navigation in the formulas, active links, export to variou s formats,
and a search engine.
In parallel, computer algebra systems have grown into huge libraries of mat h -
ematical algorithms. While the implementation of mathematical functi on s in
these systems is of te n basical l y a coding of formulas from the dictionaries men-
tioned above, the algorithms have matured to a level where many of those for-
mulas can actually be computed automatically.
⋆
This work was supported by the Microsoft Research-Inria Joint Centre.

The aim of the DDMF is to combine recent algorithms in computer algebra
together with web interaction into a dictionary of mathematical functions that
is automatically generated, easily navigable with export to various formats, and
interactive
1
. Interactivity means that formulas or graphics can be adapted to the
user’s n eed s; that arbitrary precision can be given on demand; and that proofs
can be displayed if desired.
At this stage, the reader is encouraged to have a look at the DDMF at the
following url
http://ddmf.msr-inria.inria.fr
A typical page is presented in Figure 1.
The rest of this article presents the ideas un de r ly i ng our current version (1.5),
first from the point of vie w of the document system and then from the computer
algebra viewpoint.
2 Dynamic Mathematics on the Web
The language we use to produce the DDMF is called DynaMoW for Dynamic
Mathematics on the Web. The main principle on which it is based is captured
by the following statement:
The document being generated by the symbolic computation en gine is an
object of the language.
Thus, instead of using a fixed template whose fields are filled in during a com-
putation, the structure of t he document itself depends on the results of inter-
mediate computations. For instance, the number of subsections on asymptotic
expansions is a re su lt of computing the singularities of the function; the sect i on
on sy mme t ri es onl y occurs if the function has been proved even or odd.
DynaMoW is a layer between a symboli c computation engine
2
and a web
server. It lets one mix symbol i c code together with pieces of documents in a
single source code in a natural way. This provides an eas y way to showcase
computer algebra algorithms to users who do not know the syntax of a computer
algebra system: all they need is a web browser; DynaMoW has been designed to
be produce pages compatible with the most popular ones.
Moreover, once the document becomes part of th e computation, new pos-
sibilities arise. For instance, being able to glue together pi e ces of documents
during t he computation lets us turn a trac e of the computation into a detailed
mathematical proof of its result. ( S ee, for instance, the proof of the recurrence
formula for the coefficients of the Taylor series of the Airy Ai function.) This
answers a frequent reques t of users of computer algebra systems, who want to
be able to understand where the results come from an d how they can check or
trust them. Traces are not the only type of proof that can be generated. For
1
An ancestor of these ideas without interactivity was presented in [10].
2
Currently we use Maple, but DynaMoW is designed so th at other systems can be
used as well.
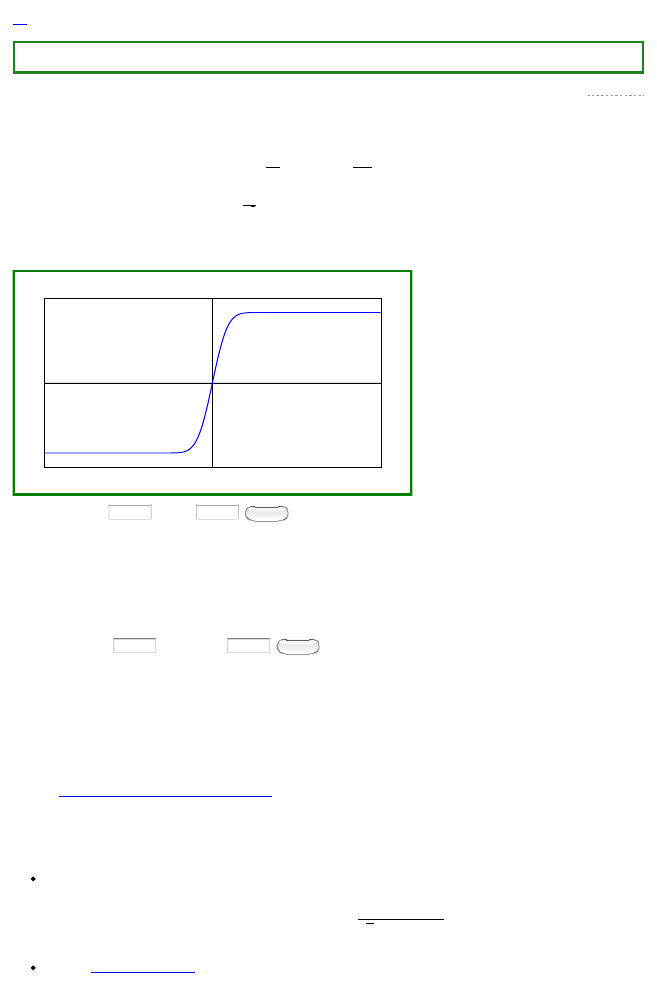
The Special Function
1. Differential equation
The function satisfies
with initial values , .
2. Plot of
-10 10
-1.2
1.2
min = max =
3. Numerical Evaluation
(Below, path may be either a point or a broken-line path along which to perform analytic continuation of the solution of
the defining differential equation. Each should be of the form x + y*i .)
path = precision =
4. Symmetry
The function is odd:
for all complex numbers .
See the .
5. Taylor expansion of at 0
Expansion of erf at :
See the for the coefficients of the Taylor expansion.
erf x
( )
erf x( )
2 y y
!
d
dx
x( )
"
x +
d
2
dx
2
x( ) = 0
y 0( ) = 0 y (
0
) 0( ) = 2
1
p
!
erf x
( )
erf :29339518 :26991350 1=4 =4( + 1 i) ! 0 + 0 i
z [z ; ; ]
1
z
2
: : : ; z
n
z
k
erf x( )
erf erf x( ) = " "x( )
x
erf x
( )
0
erf x( ) =
X
1
n=0
2
"1( )
n
x
2 +1n
!
p
! 2( n + 1) n
url
-10
10
Submit
1/4+1/4*i
8
Submit
Proof That the Function is Odderf x( )
recurrence relation
change rendering
Fig. 1. The begining of the page of the DDMF on the error function
instance, we may present a simple proof for the solution of a recurrence once the
solution has been found, instead of retracing its computation.
The implementation of the DynaMoW language itself is work in progress and
a stable version will be described in due course. We believe that this language
will be of interest outside of the DDMF. For instance, we have also used it with
success for an enc y cl opedia of combinatorial structures.
3 Computer Algebra Algorithms
From the computer algeb ra point of view, what is a good definit ion of a math-
ematical function s uch that all the desired formulas can be computed algorith-
mically? Our choice is to concentrate on
Functions given as solutions of linear differenti al equations or linear re-
currences.
Our basic data-structure consists of these equat i ons and their initial conditions.
In th e examp l e of Fig. 1, this is the content of Section 1.
This data-structure has become common in computer algebra, starti ng with
works of S tan l ey [17], Lipschitz [9], Zeilberger [18] and more recently Chyz ak ,
Salvy et alii [4,5, 6]. In particular, we rely on the Maple gfun package [16] for
many of our compu t at i ons .
Given this data structure, we have used or developed algorithms to compute
many relevant properties of mathematical functions. For instance, Section 3 of
our example offers numerical approximations of guar anteed quality in good com-
plexity (see [11] for the algorithm). Such approximations can b e used to produce
graphs as in Section 2 of the example. Section 5 is based on recurrences for t h e
Taylor coefficients that are obtained from the d iff er ential equations. When they
exist, closed-form hypergeometric solutions of these recurrences can be com-
puted [14]. In all cases, the rest of that Section 5 (beyond the part that is visible
in Fig. 1) gives the first terms of these expansions and bounds on tails of power
series [12]. The same comput at i on s are performed at each singularity includ-
ing infinity. Further results include Chebyshev e x pan si on s [2] and diffe re ntial
equations for the Laplace transform (Sections 7 and 8).
Future Work
Some of our next steps include these tasks: automatic handling of families of
functions or functions with parameters, like the Bessel functions, either by let-
ting the user ch oose values for the paramete rs , or by performing an automatic
discussion according to the possible range of values; automatic generation of
good numerical code at fixed precision; more integral transforms ; expansions on
other bases; information on the zeros of the functions; handling of branch-cuts;
and su p port for user-defined functions.
References
1. Abramowitz, M., Stegun, I.A. (eds.): Handbook of mathematical functions with
formulas, graphs, and mathematical tables. Dover Pu b li c a ti o n s In c . , New York
(1992), reprint of the 1972 edition. First edition 1964
2. Benoit, A., Salvy, B.: Chebyshev expansions for solutions of linear differential equa-
tions. In: May, J. (ed.) Symbolic and Algebraic Computation. pp. 23–30. ACM
Press (2009), proceedings of ISSAC’09, Seoul, July 200 9
3. Boisvert, R., Lozier, D.W.: A Century of Excellence in Measurements S ta n d a rd s
and Technology, chap. H a n d book of Mathematical Functions, pp. 135–139. CRC
Press (2001)
4. Chyzak, F.: Groebner bases , symbolic summation and symbo l ic integration. In:
Buchberger, B., Winkler, F. (eds.) Groebner Bases and Applica ti o n s (Proc. of the
Conference 33 Years of Gr¨obner Bases). London Mathematical Society Lecture
Notes Series, vol. 251, pp. 32–60. Cambridge University Press (1998), ISBN 0-521-
63298-6
5. Chyzak, F.: An e xt en si o n of Zeilberger’s fast algorithm to general holonomic func-
tions. Discrete Mathematics 217(1-3), 115–134 (2000)
6. Chyzak, F., Kauers, M., Salvy, B.: A non-holonomic systems approach to special
function identities. In: May, J. (ed.) Symbolic a n d Algebraic Computation. pp.
111–118. ACM Press (2009), proceedings of ISSAC’09, Seoul, July 2009
7. Erd´elyi, A.: Higher Transcendental Functions, vol. 1–3. R. E . Krieger publishing
Company, Inc., Malabar, Florida, second edn. (1981). First edit io n 19 5 3
8. Gradshteyn, I.S., Ryzhik, I.M.: Table of I ntegrals, Series, and Products. Academic
Press (1996). First English edition 1965
9. Lipshitz, L.: D-finite power series. Journal of Algebra 122(2), 353–373 (1989)
10. Meunier, L., Salvy, B.: ESF: An automatically generated encyclopedia of special
functions. In: Sendra, J.R. (ed.) Symbolic and Algebraic Computation. pp. 199–
205. ACM Press (2003), proceedings of ISSAC’03, Phi la d el p h ia , Aug u s t 20 0 3
11. Mezzarobba, M.: NumGfun: a package for numerical and analytic comp u t a t io n with
D-finite functions. In: ISSAC’10. ACM Press, http://arxiv.org/abs/1002.3077
12. Mezzarobba, M., Salvy, B.: Effective bounds for P-recursive sequences. Journal of
Symbolic Computation (To appear)
13. Olver, F.W.J., Lozier, D.W., Boisvert, R.F., Clark, C.W. (eds.): NIST Handbook
of Mathematical Functions. Cambridge University Press (2010).
14. Petkovˇsek, M.: Hypergeometric solutions of linear recurrences with polynomial
coefficients. Journal of Symbolic Computation 14 ( 2 - 3) , 2 4 3– 2 6 4 (1 9 9 2)
15. Prudnikov, A.P., Brychkov, Y.A., Marichev, O.I.: Integrals and Series. Volume 1–6.
First edition in Moscow, Nauka, 1981
16. Salvy, B., Zimmermann, P.: Gfun: a Maple package for the manipulation o f gener-
ating and holonomic functions in one variable. ACM Transactions on Mathematical
Software 20(2) , 16 3 – 1 7 7 (19 9 4 )
17. Stanley, R.P.: Differentiably finite power series. European Journal of Combinatorics
1(2), 175–188 (1980)
18. Zeilberger, D.: A holonom ic systems approa ch to special functions identities. Jour-
nal of Computational and Applied Mathematics 32(3), 321–36 8 (1 9 9 0 )
