1
Pincer-Based vs. Same-Direction Strategies of
Search for Smart Evaders by Swarms of Agents
Roee M. Francos and Alfred M. Bruckstein
Abstract—Suppose in a given planar region, there are smart
mobile evaders and we want to detect them using sweeping
agents. We assume that the agents have line sensors of equal
length. We propose procedures for designing cooperative sweep-
ing processes that ensure successful completion of the task,
thereby deriving conditions on the sweeping speed of the agents
and their paths. Successful completion of the task means that
evaders with a known limit on their speed cannot escape the
sweeping agents. A simpler task for the sweeping swarm is the
confinement of the evaders to their initial domain. The feasibility
of completing these tasks depends on geometric and dynamic
constraints that impose a lower bound on the speed the sweeping
agent must have. This critical speed is derived to ensure the
satisfaction of the confinement task. Increasing the speed above
the lower bound enables the agents to complete the search task
as well. We present a quantitative and qualitative comparison
analysis between the total search time of same-direction sweep
processes and pincer-movement search strategies. We evaluate the
different strategies by using two metrics, total search time and
the minimal critical speed required for a successful search. We
compare two types of pincer-movement search processes, circular
and spiral, with their same-direction counterparts, for any even
number of sweeping agents. We prove that pincer based strategies
provide superior results in all practical scenarios and that the
spiral pincer sweep process allows detection of all evaders while
sweeping at nearly theoretically optimal speeds.
I. INTRODUCTION
T
HE aim of this work is to provide an efficient ”must-
win” search policy for a swarm of n sweeping agents
that must guarantee detection of an unknown number of smart
evaders initially residing inside a given circular region of
radius R
0
while minimizing the search time. The evaders move
and try to escape the initial region at a maximal speed of
V
T
, known to the sweepers. All sweepers move at a speed
V
s
> V
T
and detect the evaders using linear sensors of
length 2r. Each ”must-win” policy requires a minimal speed
that depends on the trajectory of the sweepers. Finding an
efficient algorithm requires that, throughout the sweep, the
footprint of the sweepers’ sensors maximally overlaps the
evader region (the region where evaders may possibly be).
This work develops two ”must-win” same-direction search
strategies, circular and spiral, for a swarm consisting of an
even number of searchers that sweep the evader region until
all evaders are detected. Afterwards, a comparison between the
developed same-direction and pincer-based search strategies
developed in [1] is performed.
Roee M. Francos and Alfred M. Bruckstein are with the Faculty of Com-
puter Science, Technion- Israel Institute of Technology, Haifa, Israel, 320003,
A. Overview of Related Research
Several interesting search problems originated in the second
world war due to the need to design patrol strategies for
aircraft aiming to detect ships or submarines in the English
channel, see [2]. The problem of patrolling a corridor using
multi agent sweeping systems in order to ensure the detection
and interception of smart targets was also investigated in [3]
and provably optimal strategies were provided in [4].
In [5], [6], Bressan et al. investigate optimal strategies for
the construction of barriers in real time aiming at containing
and confining the spread of fire from a given initial area of
the plane. The authors are interested in determining a minimal
possible barrier construction speed that enables the confine-
ment of the fire, and on determining optimality conditions for
confinement strategies.
A non-escape search procedure for evaders that are origi-
nally located in a convex region of the plane and may move out
of it is investigated in [7], and a cooperative progressing spiral-
in algorithm performed by several agents with disk shaped
sensors in a leader-follower formation is proposed. In [8],
McGee et al. also investigate a search problem for smart
targets that do not have any maneuverability restrictions except
for an upper limit on their speed. The sensor the agents are
equipped with detects targets within a disk shaped area around
the searcher location. Search patterns consisting of spiral and
linear sections are considered. In [9], Hew proposes searching
for smart evaders using concentric arc trajectories with agents
sensors similar to [8]. Such a search is aimed at detecting
submarines in a channel or in a half plane.
Another set of related problems are pursuit-evasion games,
where the pursuers’ objective is to detect evaders and the
evaders objective is to avoid the pursuers. Pursuit-evasion
games include combinations of single and multiple evaders and
pursuers scenarios. In this context several works considered
the problem of defending a region from the entrance of
intruders. In [10], [11], such problems are investigated under
the name of “reach-avoid games”. These types of problems
were also addressed in the context of perimeter defense games
by Shishika et al. in [12], [13], with a focus on utilizing
cooperation between pursuers to improve the defense strategy.
In [12], implicit cooperation between pairs of defenders that
move in a “pincer movement” is performed in order to
intercept intruders before they enter a convex region in the
plane. In [14], pursuit–evasion problems involving multiple
pursuers and multiple evaders (MPME) are studied. Pursuers
and evaders are all assumed to be identical, and pursuers
follow either a constant bearing or a pure pursuit strategy.
The problem is simplified by adopting a dynamic divide and
arXiv:2104.06940v2 [cs.MA] 15 May 2022
2
conquer approach, where at every time instant each evader
is assigned to a set of pursuers based on the instantaneous
positions of all the players. The original MPME problem is
decomposed to a sequence of simpler multiple pursuers single
evader (MPSE) problems by classifying if pursuer is relevant
or redundant for each evader by using Apollonius circles. Only
the relevant pursuers participate in the MPSE pursuit of each
evader.
In [15], the confinement and cleaning tasks for a line
formation of agents or alternatively for a single agent with
a linear sensor are analyzed. In [1], teams of agents perform
pincer sweep search strategies with linear sensors.
Recent surveys on pursuit evasion problems are [16]–[18].
In [16], a taxonomy of search problems is presented. The
paper highlights algorithms and results arising from different
assumptions on searchers, evaders and environments and dis-
cusses potential field applications for these approaches. The
authors focus on a number of pursuit-evasion games that are
directly connected to robotics and not on differential games
which are the focus of the other cited surveys. [17] presents
a survey on pursuit problems with 1 pursuer versus 2 evaders
or 2 pursuers versus 1 evader are formulated as a dynamic
game and solved with general methods of zero-sum differential
games. In [18], the authors present a recent survey on pursuit-
evasion differential games and classify the papers according
to the numbers of participating players: single-pursuer single-
evader (SPSE), MPSE, one- pursuer multiple-evaders (SPME)
and MPME.
B. Contributions
In this paper, we provide several theoretical and experimen-
tal contributions to multi-agent search and coordinated motion
planning literature. We propose search protocols that guarantee
detection of all smart evaders that are initially located in given
circular region from which they may move out of in order to
escape the pursuing sweeping agents. A detailed theoretical
analysis of trajectories, critical speeds and search times for
same-direction sweep protocols performed by a swarm of n
cooperative agents are developed in order to quantitatively
compare these methods to the pincer-based protocols described
in [1].
• We propose two types of same-direction sweep protocols:
– Same-direction circular sweep pincer sweep strategy
– Same-direction spiral sweep pincer sweep strategy
• We prove that for both same-direction sweep protocol
types, the corresponding pincer-based protocols yield a
lower critical speed.
• We show that the circular pincer-based sweep protocol
always results in shorter sweep times compared to its
same-direction counterpart.
• Results show that as the number of sweepers increases,
circular pincer-based protocols require a smaller critical
speed even when compared to spiral same-direction pro-
tocols. This result indicates that although implementing
pincer-based circular search protocols requires sweepers
with more basic capabilities compared to spiral proto-
cols, the cooperation between the sweepers considerably
improves the overall performance of the sweeper team.
• We experimentally show that for all choices of search
parameters the spiral pincer-based protocol is favourable
compared to its same-direction counterpart and that it
results in critical speeds that approach the theoretical
lower bound.
II. SAME-DIRECTION VERSUS PINCER-BASED SWEEPS
This paper considers a scenario in which a multi-agent
swarm of identical agents search for mobile targets or evaders
that are to be detected. The information the agents perceive
only comes from their own sensors, and all evaders that
intersect a sweeper’s field of view are detected. We assume
that all agents have a linear sensor of length 2r. The evaders
are initially located in a disk shaped region of radius R
0
.
There can be many evaders, and we consider the domain to be
continuous, meaning that evaders can be located at any point in
the interior of the circular region at the beginning of the search
process. All sweepers move with a speed of V
s
(measured at
the center of the linear sensor). By assumption the evaders
move at a maximal speed of V
T
, without any maneuverability
restrictions. The sweeper swarm’s objective is to ”clean” or to
detect all evaders that can move freely in all directions from
their initial locations in the circular region of radius R
0
.
Search time clearly depends on the type of sweeping
movement the searching team employs. Detection of evaders is
based on deterministic and preprogrammed search protocols.
We consider two types of search patterns, circular and spiral
patterns. The desired result is that after each sweep around the
region, the radius of the circle that bounds the evader region
(for the circular sweep), or the actual radius of the evader
region (for the spiral sweep), decreases by a strictly positive
value. This guarantees complete cleaning of the evader region,
by shrinking in finite time the possible area in which evaders
can reside to zero. At the beginning of the circular search
process we assume that only half the length of the agents’
sensors is inside the evader region, i.e. a footprint of length
r, while the other half is outside the region in order to catch
evaders that may move outside the region while the search
progresses. At the beginning of the spiral search process we
assume that the entire length of the agents’ sensors is inside
the evader region, i.e. a footprint of length 2r.
In the single agent search problem described in [15], we
observed that there can be escape from point P = (0, R
0
)
(shown in Fig. 1 (a)), when basing the searcher’s speed only
on a single traversal around the evader region. Therefore we
had to increase the agent’s critical speed to deal with this
possible escape. Point P is considered as the ”most dangerous
point”, meaning that it has the maximum time to spread
during sweeper movement, hence if evaders spreading from
this point are detected, evaders escaping from all other points
are detected as well. If we choose to distribute a multi-agent
swarm equally along the boundary of the initial evader region,
we would have the same problem of possible escape from the
points adjacent to the starting locations of every sweeper.
In [1] we proposed an alternative method for multi-agent
sweep processes such that pairs of sweeping agents move out
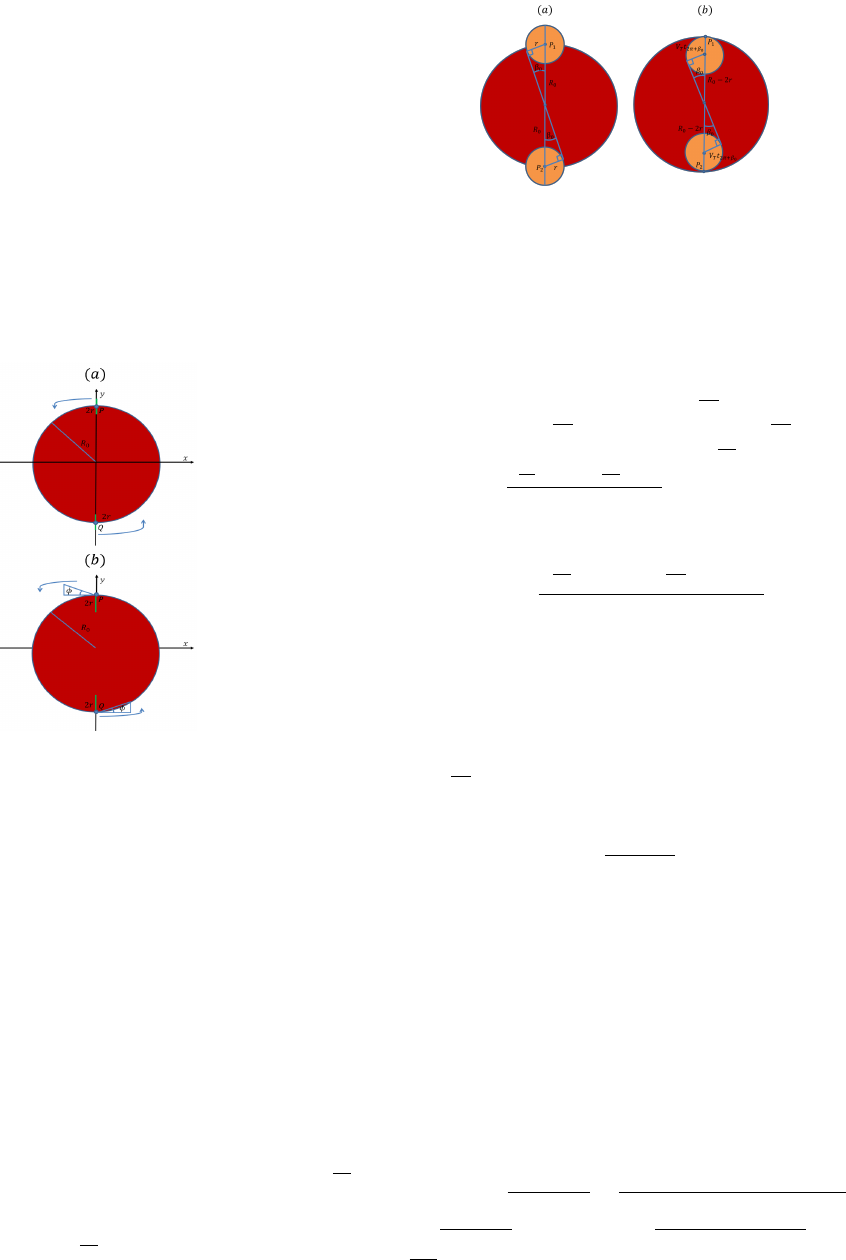
3
in opposite directions along the boundary of the evader region
and sweep in a pincer movement rather than having a convoy
of sweepers all moving in the same-direction along the bound-
ary. The proposed method is applicable for any even number of
sweepers. The sweepers are initially positioned in pairs back
to back. One sweeper in the pair moves counter clockwise
while the other sweeper in the pair moves clockwise. Once
the sweepers meet, i.e. their sensors are again superimposed
at a meeting point, they switch the directions in which they
move. This changing of directions occurs every time a sweeper
bumps into another. Each sweeper is responsible for an angular
sector of the evader region that is proportional to the number
of participating agents in the search. Sweeping with a pincer-
based search protocol eliminates the need to sweep additional
areas to detect evaders from these additional ”most dangerous
points” since in pincer-based protocols the ”most dangerous
points” are now located at the tips of their sensors closest to
the evader region’s center.
Fig. 1. (a) - Initial placement of 2 agents employing the same-direction
circular sweep process. (b) - Initial placement of 2 agents employing the same-
direction spiral sweep process. The sweepers sensors are shown in green. The
angle φ is the angle between the tip of a sweeper’s sensor and the normal of
the evader region. φ is an angle that depends on the ratio between the sweeper
and evader speeds.
.
III. SAME-DIRECTION CIRCULAR SWEEP
A. Circular Sweep Time Calculation
Previously in [15] we tried to find the tightest lower bound
of a searcher’s speed by constructing a function of 2 variables
f(t, V
s
), by demanding that the furthest possible spread of the
evader region is cleaned by the furthest tip of the sweeper’s
line sensor. A lesser requirement is to demand that by the
time the most problematic point in the evader region, point
P , spreads to a possible circle of radius of r around point P ,
the sweeping swarm completes in addition to a sweep of
2π
n
around the evader region an additional angular traversal that is
proportional to traversing an arc of length r. This means that
the agent travels an angle of
2π
n
+β
0
where β
0
is marked in Fig.
2(a). This assumption results in a simplified expression for the
critical speed that bounds the previously found critical speed
of [15] from above for all choices of geometric parameters.
We denote the time it takes the most problematic points to
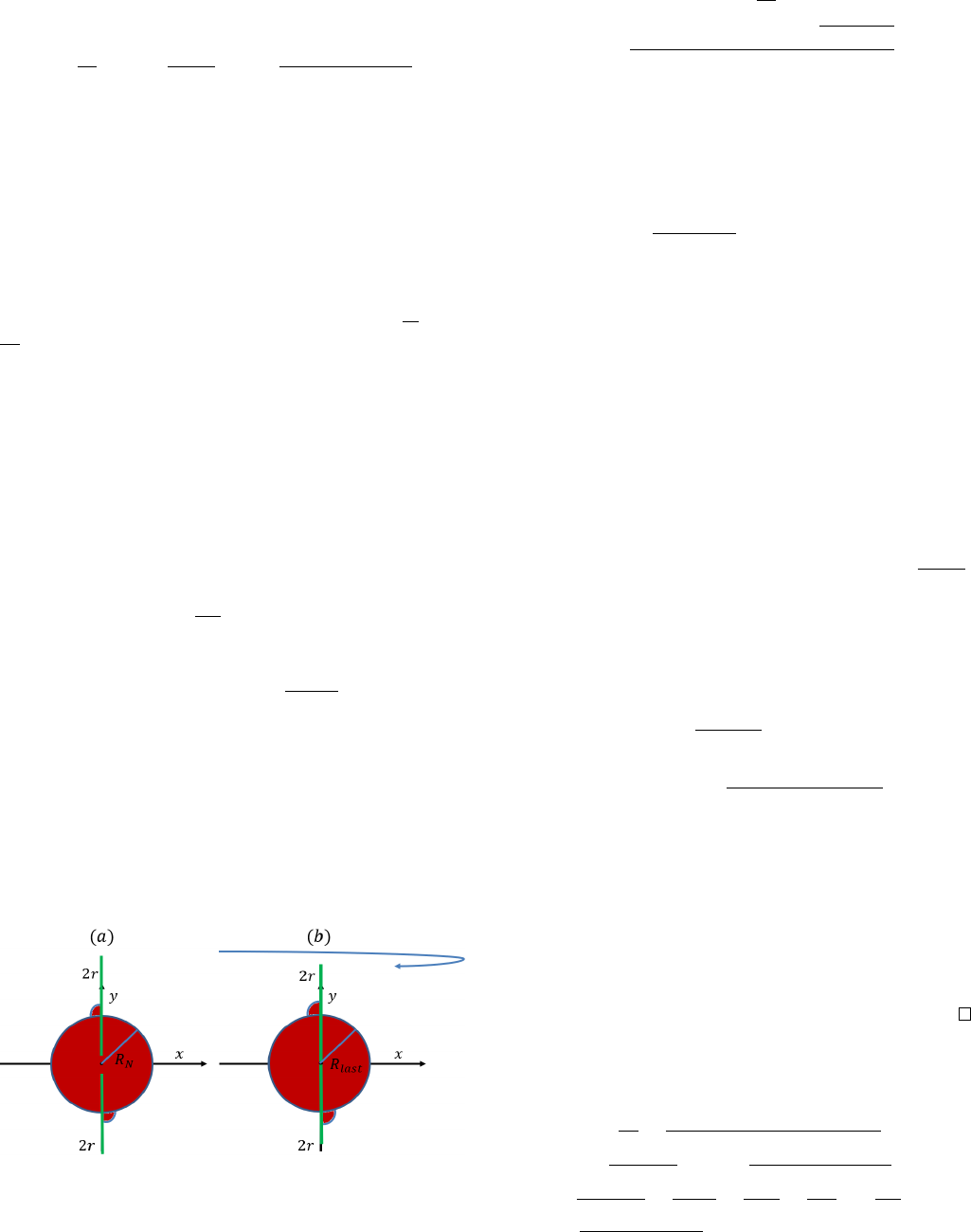
Fig. 2. Geometric representation required for critical speed calculation. Red
areas indicate locations where potential evaders may be located. The orange
circles denote the spread of potential evaders around the most problematic
points P
1
and P
2
during a traversal of 2π + β
0
around the evader region. (a)
- Same direction circular sweep. (b) - Same direction spiral sweep.
spread a distance of r as T
e
. These points are adjacent to the
starting locations of the sweepers, and 2 such points P
1
and
P
2
, exist in case the search is performed with 2 sweepers, as
shown in Fig. 2. We have that T
e
=
r
V
T
. We can see from
Fig. 2. that sin β
0
=
r
R
0
, therefore β
0
= arcsin
r
R
0
. The time
it takes the sweeper to travel an angle of
2π
n
+ β
0
is therefore
given by T
s
=
2π
n
+arcsin
r
R
0
R
0
V
s
. In order to guarantee no
escape, we demand that T
s
≤ T
e
. Therefore, rearranging terms
in the previous equation and plugging T
e
instead of T
s
yields,
V
c
≥
2π
n
+ arcsin
r
R
0
R
0
V
T
r
(1)
The lower bound on a sweeper speed that ensures confinement
is obtained when we have equality in (1). In future derivations
we use the first order Taylor approximation for the arcsine
function in (1), in order to enable the construction of analytical
results for the sweep times of the evader region. Such an
approximation is valid since in all practical scenarios the ratio
between
r
R
0
is sufficiently small. Applying this approximation
to (1) allows us to define V
c
circ
, the chosen critical speed,
given by,
V
c
circ
=
2πR
0
V
T
rn
+ V
T
(2)
In order for the sweeper swarm to advance inward toward the
center of the evader region it must travel in a speed that is
greater than the critical speed. We denote by ∆V > 0 the
increment in the sweeping agents’ speed that is above the
critical speed. Each agent’s speed V
s
is therefore given by the
sum of the critical speed and ∆V , namely V
s
= V
c
circ
+ ∆V .
The total sweep times it takes the sweeper swarm to reduce the
evader region to a region bounded by a circle with a radius that
is smaller or equal to r is given by the sum of the circular
motions and inward advancements that are performed after
the completion of each circular sweep. The time it takes the
sweepers to perform the circular sweeps is given by,
T
circular
= −
R
0
(V
s
+V
T
)
V
s
V
T
+
r(V
s
−V
T
)(n(V
s
+V
T
)+2πV
T
N
n
)
2πV
T
2
V
s
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
(V
s
+ V
T
)
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
2
V
s
+
2πr
nV
s
(3)
4
The time it takes the sweepers to perform the inward advance-
ment is given by,
T
in
=
R
0
V
s
+
1 +
2πV
T
V
s
+V
T
N−1
2πR
0
V
T
−r(V
s
−V
T
)
V
s
(V
s
+V
T
)
(4)
The full analytical development is provided in Appendix A.
B. Same-direction Circular Sweep End-game
In order to entirely clean the evader region the sweepers
need to change the scanning method when the evader region
is bounded by a circle of radius r. This is due to the fact that
a smart evader that is very close to the center of the evader
region can travel at a very high angular velocity compared to
the angular velocity of the pursuing agents. This constraint
is described by the following two equations, ω
s
=
V
s
r
, ω
T
=
V
T
ε
. The first describes the searcher’s angular velocity and the
second the evader’s angular velocity. Since ε can be arbitrarily
small the evader can move just behind a sweeper’s sensor and
never be detected. Thus a slight modification to the sweep
process needs to be applied in order to clean the entire evader
region with the sweeper swarm that employs a circular scan.
After completing sweep number N
n
− 1 the sweepers move
toward the center of the evader region until the tip of the
sweeper’s sensors closest to the center of the evader region are
placed at the center of the evader region. Following this motion
the sweepers perform a circular sweep of radius r around the
center of the evader region. The time this last circular sweep
takes is given by T
last
=
2πr
nV
s
. Therefore, after the last circular
scan the evader region is bounded by a circle of radius R
last
,
given by,
R
last
= T
last
V
T
=
2πrV
T
nV
s
(5)
In order to overcome the challenges in the circular search that
were described we propose that after scan number N
n
+ 1
the sweeper swarm will travel to the right until cleaning
the wavefront that propagates from the right portion of the
remaining evader region and then travel to the left until
cleaning the remaining evader region. A depiction of the
scenario at the beginning of the end-game is presented in Fig.
3. Theorem 1 states the conditions for this demand to hold.
Fig. 3. Depiction of the end-game steps for the same-direction circular sweep
performed by 2 sweepers. The sweepers sensors’ are shown in green and
red areas indicate locations where potential evaders may still be located.
(a) - Evader region status and sweepers’ locations prior to the last inward
advancement. (b) - Evader region status and sweepers’ locations prior to the
linear sweep.
Theorem 1. When defining α =
R
0
r
, if ∆V satisfies that,
∆V ≥
−4πV
T
α + πV
T
+ V
T
√
π
2
+ 8πn
2n
(6)
then the evader region will be completely cleaned by n
sweepers that employ the linear scan after N
n
+ 1 iterations.
Proof. During the previously mentioned movement the margin
between the tip of the sensor in each direction to the evader
region boundaries must satisfy,
2r − R
last
V
T
> T
linear
(7)
in order to guarantee no escape. T
linear
denotes the time it
takes the sweepers to clean the right section of the remaining
evader region in addition to the time it takes them to scan
from the rightmost point they got to until the leftmost point
of the expansion. These times are respectively denoted as t
and
˜
t. Therefore, T
linear
is given by T
linear
=
˜
t + t. The
evader region’s rightmost point of expansion starts from the
point (R
last
, 0) and spreads at a speed of V
T
. Therefore, if
the constraint in (7) is satisfied we can view the rightward
and leftward linear sweeps as a one dimensional scan. This
geometric constraint can be observed in Fig. 3. Therefore, the
time t it takes the sweepers to clean the spread of potential
evaders from the right section of the region can be calculated
from, V
s
t = R
last
+V
T
t. Therefore, t is given by, t =
R
last
V
s
−V
T
.
˜
t is computed by calculating the time it takes the sweepers
located at point (tV
s
, 0) to change their scanning direction
and perform a leftward scan to a point that spread at a speed
of V
T
from the leftmost point in the evader region at the origin
of the search, the point (−R
last
, 0), for a time given by
˜
t + t.
We have that, −R
last
− V
T
˜
t + t
= tV
s
− V
s
˜
t. Plugging in
the value of t yields
˜
t =
2V
s
R
last
(V
s
−V
T
)
2
. T
linear
is therefore given
by,
T
linear
= t +
˜
t =
6πrV
T
V
s
− 2πrV
T
2
nV
s
(V
s
− V
T
)
2
(8)
Therefore, the total scan time until a complete cleaning of the
evader region is given by T
total
= T
circular
+ T
in
+ T
linear
.
For the one dimensional scan to be valid and ensure a non
escape search and complete cleaning of the evader region (7)
must be satisfied. This demand implies that for a given α, the
designer of the sweep process can infer which ∆V needs to
be chosen in order to satisfy (6) and thus completely clean
the evader region using the final linear sweeping motion. For
a complete derivation see Appendix B.
Theorem 2. For a valid circular search process the total
search time until a complete cleaning of the evader region
is given by, T = T
circular
+ T
in
+ T
linear
, or as,
T = −
R
0
V
T
+
r(V
s
−V
T
)(n(V
s
+V
T
)+2πV
T
N
n
)
2πV
T
2
V
s
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
−1
2πR
0
V
T
−rn(V
s
−V
T
)
V
s
1
n(V
s
+V
T
)
+
V
s
2πV
T
2
+
1
2πV
T
+
1
nV
T
+
2πr
nV
s
+
6πrV
T
V
s
−2πrV
T
2
nV
s
(V
s
−V
T
)
2
(9)

5
10 20 30
0
100
200
300
400
Number of Agents
Time
∆V =0.5V
T
∆V =2V
T
∆V =5V
T
∆V =15V
T
Fig. 4. Total search times until complete cleaning of the evader region. We
simulated sweep processes with an even number of agents, ranging from
2 to 32 agents, that employ the multi-agent same-direction circular sweep
processes. We show results obtained for different values of speeds above the
circular critical speed. The chosen values of the parameters are r = 10,
V
T
= 1 and R
0
= 100.
IV. SAME-DIRECTION SPIRAL SWEEP
A. Spiral Sweep Time Calculation
Since our aim is to provide a sweep process that improves
the same-direction circular sweep process we would like
the sweepers to employ a more efficient motion throughout
the sweep process. Therefore, we wish that throughout the
motion of the sweepers, their sensors’ footprint will maximally
overlap the evader region. This can be obtained by a spiral
scan, where the sweepers’ sensors track the expanding evader
region’s wavefront, while preserving its shape to be as close as
possible to a circle. An illustration of the initial placement of 2
sweepers that employ the same-direction spiral sweep process
is presented in Fig. 1(b). The sweepers start with a sensor
length of 2r inside the evader region. If the sweeper agents’
speed is above the scenario’s critical speed, the sweepers
reduce the evader region’s area after completing a traversal
around the region. Each sweeper begins its spiral traversal
with the tip of its sensor that is furthest from the center of
the evader region, in a position that is tangent to the boundary
of the evader region. In order to keep their sensors tangent to
the evader region, the sweepers must travel at angle φ to the
normal of the evader region. φ is calculated from sin φ =
V
T
V
s
This method of traveling at angle φ preserves the evader
region’s circular shape and is described thoroughly in [1].
Contrary to the pincer-based strategy where each sweeper
travels only an angle of
2π
n
at each sweep iteration, in same-
direction sweeps, each sweeper travels a larger angle than
2π
n
at each iteration around the evader region in order to detect
all escaping smart evaders. The additional angle, denoted by
β, needs to be traversed in order to detect all evaders that
may have spread from the ”most dangerous points” at the
beginning of each sweep. Such points are adjacent to the
starting locations of every sweeper. The angle β depends on
the radius of the circle that bounds the evader region. After a
sweeper traverses the additional angle β, the evader region’s
boundary is due to spread from points that resided at the lower
tips of the sensors. When the tips of the sensors leave these
points, evaders may spread from them in all directions at a
speed of V
T
. The time it takes a sweeper to travel an angle of
2π
n
+ β
0
, where β
0
is shown in Fig. 2(b) is given by,
t
2π
n
+β
0
=
(R
0
− r)
e
(
2π
n
+β
0
)
V
T
√
V
s
2
−V
T
2
− 1
V
T
(10)
The method of deriving this equation follows similar steps as
in section V of [1]. The subscript 0 in β
0
denotes the iteration
or cycle number, indicating that the value of β changes as
the sweep process progresses. After a sweeper completes a
traversal of
2π
n
+β
0
around the evader region it moves towards
the center of the evader region. During this motion its lower
tip points to the center of the region. β
0
is given by,
sin β
0
=
V
T
t
2π
n
+β
0
R
0
− 2r
(11)
After a sweeper traverses
2π
n
+ β
0
around the evader region
the evader region’s boundary is due to evaders that originated
from the next ”most dangerous points”. The critical speed that
satisfies the confinement task is computed numerically using
the Newton method. When the sweepers travel towards the
center of the evader region after completing a spiral sweep
they have to meet the evader wavefront travelling outwards the
region with a speed of V
T
at the previous radius R
0
. Therefore,
the expansion of the evader region after the first sweep at time
t
2π
n
+β
0
, has to satisfy that,
V
T
t
2π
n
+β
0
≤
2rV
s
V
s
+ V
T
(12)
The critical speed is obtained when we have equality in (12).
In order to calculate β
0
that is obtained when the sweepers
move at the critical speed, the expression of V
T
t
2π
n
+β
0
in (12)
is substituted with its equivalent expression in (11). Hence β
0
is,
β
0
= arcsin
2rV
s
(V
s
+ V
T
) (R
0
− 2r)
(13)
Substituting the expression for t
2π
n
+β
0
, yields
(R
0
− r)
e
(
2π
n
+β
0
)
V
T
√
V
s
2
−V
T
2
− 1
=
2rV
s
V
s
+ V
T
(14)
In order to solve for V
s
we write (14) as,
F (V
s
) =
2rV
s
V
s
+ V
T
− (R
0
− r)
e
(
2π
n
+β
0
)
V
T
√
V
s
2
−V
T
2
− 1
(15)
From (15) we find V
s
using the Newton iterative root finding
method whose equation is given by,
V
s
n+1
= V
s
n
−
F (V
s
n
)
∂F (V
s
n
)
∂V
s
n
(16)
We choose as our initial estimate the lower bound on the
sweeper speed (proved in [1]) given by V
s
0
=
πR
0
V
T
nr
= V
LB
.
By using the described iterative convergence, we obtain a
solution for V
s
, which is the same-direction spiral sweep’s
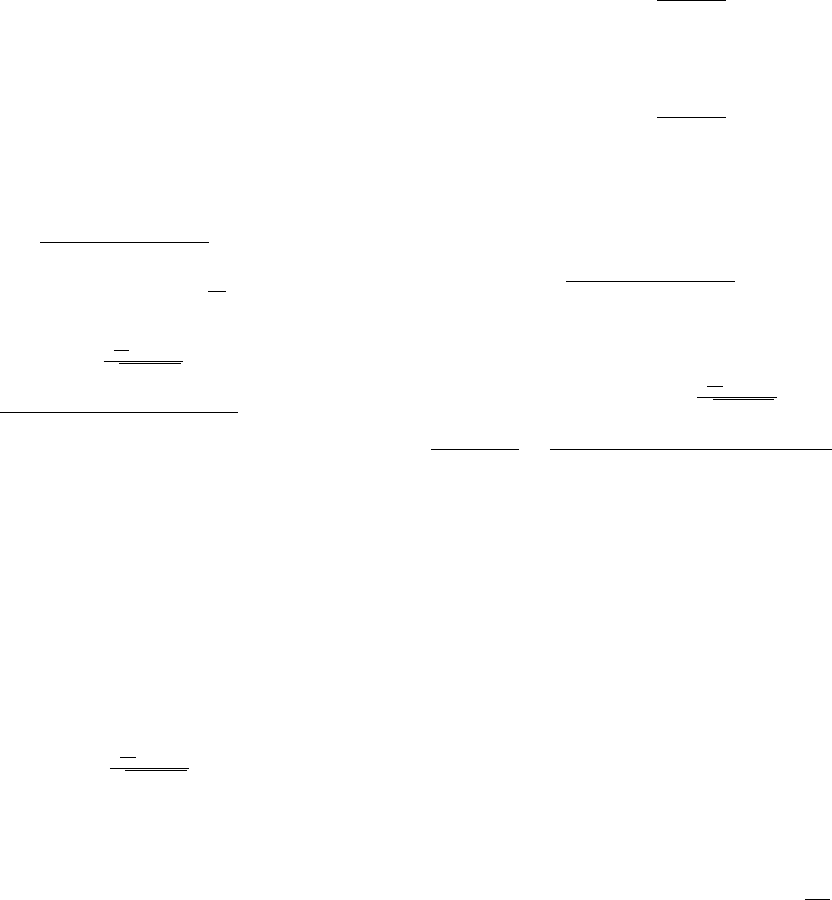
6
critical speed. We denote this speed as V
c
spiral
same
. After
converging to a solution we obtain a result that is only slightly
larger than the lower bound on the sweeper speed, V
LB
.
Let us denote by ∆V > 0 the addition to the sweeper’s
speed above the critical speed. The speed is therefore given
by, V
s
= V
c
spiral
same
+ ∆V . If a sweeper moves with a speed
greater than the critical speed, after each spiral sweep it can
advance inwards towards the center of the evader region and
sweep around an evader region that is bounded by a circle
with a smaller radius. The total search time until the evader
region is bounded by a circle with a radius that is less than
or equal to 2r is given by the sum of the total spiral sweep
times and the times of the inward advances. Namely,
T = T
in
+ T
spiral
(17)
After each iteration, the sweepers move inwards towards the
center of the evader region and the radius of the circle that
bounds the region decreases. Consequently, the angle β
i
after
which the sweepers move inwards changes as well. Therefore,
after each sweep β
i
is calculated with respect to the new radius
of the circle that bounds the evader region,
β
i
= arcsin
2rV
s
(V
s
+ V
T
) (R
i
− 2r)
(18)
The time it takes to complete a spiral sweep of
2π
n
+β
i
around
a region bounded by a circle of radius R
i
is given by,
T
spiral
i
=
(R
i
− r)
e
(
2π
n
+β
i
)
V
T
√
V
s
2
−V
T
2
− 1
V
T
(19)
Denote the distance an agent can advance towards the center of
the evader region by δ
i
(∆V ). In the term δ
i
(∆V ), ∆V denotes
the increase in the agent speed relative to the critical speed,
and i denotes the number of sweep iterations the sweepers
perform around the evader region, where i starts from sweep
number 0. This results in a new evader region bounded by a
circle with a radius of R
i+1
= R
i
− δ
i
(∆V ). We have that,
δ
i
(∆V ) = 2r − V
T
T
spirali
, 0 ≤ δ
i
(∆V ) ≤ 2r (20)
As a function of the iteration number, we have that the distance
a sweeper can advance inwards after completing an iteration
is given by,
δ
i
(∆V ) = 2r − (R
i
− r)
e
(
2π
n
+β
i
)
V
T
√
V
s
2
−V
T
2
− 1
(21)
After the sweeper completes a cycle, it moves inwards towards
the center of the evader region in a way that the inner tip of
its sensor points towards the center of the evader region with a
speed of V
s
, until it reaches the position where it starts its next
sweep at the moment it meets the evader region’s expanding
wavefront. During the inwards advancements no cleaning is
performed, while the evader region continues to spread. The
time it takes the sweeper to move inwards until its entire
sensor is over the evader region depends on the relative speed
between the sweeper’s inwards entry speed and the evader
region outwards expansion speed and is given in (25). As the
sweepers progress towards the center of the evader region, the
evader region continuous to expand. Therefore, sweepers can
only advance by a smaller distance than δ
i
(∆V ), denoted by
δ
i
ef f
(∆V ), which depends on the ratio between the speed in
which the sweeper progresses towards the center of the region
and the sum of velocities of sweeper and evader region spread.
δ
i
ef f
(∆V ) is the actual distance the sweeper moves at each
iteration in order to meet the wavefront of the evader region
when its entire sensor overlaps the evader region. Therefore,
the distance sweepers can advance inwards after completing
an iteration is given by,
δ
i
ef f
(∆V ) = δ
i
(∆V )
V
s
V
s
+ V
T
(22)
The evader region is therefore bounded by a circle with a
radius given by,
R
i+1
= R
i
− δ
i
(∆V )
V
s
V
s
+ V
T
(23)
This process continues until the evader region is bounded by
a circle with a radius that is smaller than 2r. We denote this
radius as R
N
. Once the evader region is contained inside a
circular domain with a radius of 2r < R
i
< 4r, β
i
is,
β
i
= arcsin
(R
i
− 2r) V
s
(V
s
+ V
T
) (R
i
− 2r)
(24)
The inwards advancement time depends on the iteration num-
ber. It is denoted by T
in
i
and its expression is given by,
T
in
i
=
δ
i
ef f
(∆V )
V
s
=
2r − (R
i
− r)
e
(
2π
n
+β
i
)
V
T
√
V
s
2
−V
T
2
− 1
V
s
+ V
T
(25)
During the inward advancements only the tip of the sen-
sor, that has zero width, is inserted into the evader region.
Therefore, no evaders are detected until the sweeper completes
its inward advance and starts sweeping again. This search
methodology continues until the evader region is bounded by
a circle with a radius that is less than or equal to 2r.
B. Same-direction Spiral Sweep End-game
In order to entirely clean the evader region, the sweepers
need to change the scanning method when the evader region is
bounded by a circle of radius 2r, due to the same consideration
that are described in the end-game of the same-direction
circular sweep process. The depiction of the scenario at the
beginning of the end-game is shown in Fig. 5. In the last
inward advancement, the sweepers place the tips of their
sensors at the center of the evader region. The time it takes the
sweepers to complete this movement is given by T
e
=
R
N
V
s
.
Following the last inward advancement, the sweepers per-
form the last spiral sweep when the tips of their sensors are
placed at the center of the evader region as can be seen in
Fig. 5(b). In order to apply a linear sweeping movement
the last spiral sweep has to reduce the evader region to be
bounded by a circle of radius less than 2r. Following the
last inward advancement, the sweepers performs an additional
7
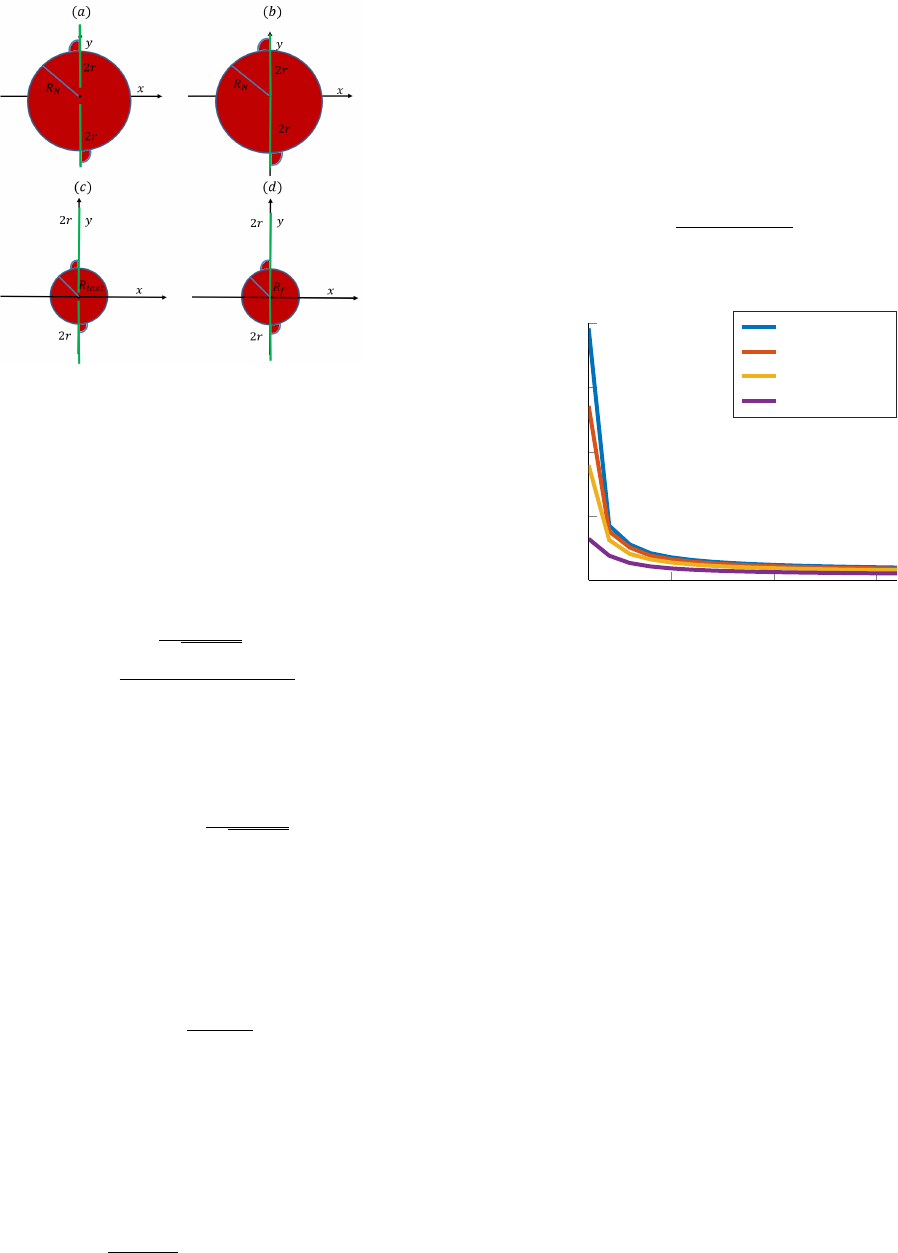
Fig. 5. Different stages of the end-game. The sweepers’ sensors are shown
in green and the evader region is shown in red. (a) - Depiction of the state
at the beginning of the end-game. (b) - Depiction of the scenario after the
sweepers move toward the center of the evader region and place the tips of
their sensors at the center of the region. (c) - Depiction of the scenario after
the last spiral sweep. (d) - Depiction of the scenario prior to the linear sweep.
spiral sweep when the center of each sweeper’s sensor is as
at a distance of r from the center of the evader region. The
time it takes to complete this sweep is denoted by T
l
and is
given by,
T
l
=
r
e
2πV
T
n
√
V
s
2
−V
T
2
− 1
V
T
(26)
The depiction after the sweepers complete this last spiral
movement can be seen in Fig. 5(c). During the last spiral
sweep, the evader region spreads from its center point to a
circle with a radius of,
R
last
= T
l
V
T
= r
e
2πV
T
n
√
V
s
2
−V
T
2
− 1
(27)
In order for a linear scan to be applicable R
last
has to
be smaller than 2r. This leads to a requirement on the
sweeper’s speed developed in Appendix C. Following this
last spiral sweep, two sweepers place the tips of their sensors
at the center of the evader region, advancing a distance of
R
in
= 2r −R
last
. The time it takes the sweepers to complete
this motion is given by T
f
=
2r−R
last
V
s
. During this time the
evaders spread to a circle of radius R
f
around the center of
the region given by R
f
= T
f
V
T
+ R
last
.
The depiction of the scenario at this time instance is shown
in Fig. 5(d). Following this movement, the sweepers perform
a linear motion and complete the search process. During the
previously mentioned movement the margin between the edge
of the sensors in each direction to the evader region boundaries
must satisfy,
2r − R
f
V
T
> T
linear
(28)
In order to guarantee no evader escapes undetected. The
development of the linear sweep time follows the same steps as
in the end-game section of the same-direction circular sweep
when replacing R
f
instead of R
last
. Therefore, the total scan
time until a complete cleaning of the evader region is given
by,
T
total
= T
spiral
+ T
in
+ T
e
+ T
l
+ T
f
+ T
linear
(29)
For the one dimensional scan to be valid and ensure a non
escape search and complete cleaning of the evader region,
(28) must be satisfied. This demand results in the following
requirement on V
s
,
V
s
≥
2rV
T
+ V
T
R
f
2r − R
f
(30)
For proof see Appendix D.
10 20 30
0
50
100
150
200
Number of Agents
Time
∆V = 0.5V
T
∆V = 2V
T
∆V = 5V
T
∆V = 15V
T
Fig. 6. Total search times until complete cleaning of the evader region. We
simulated sweep processes with an even number of agents, ranging from 2 to
32 agents, that employ the same-direction spiral sweep processes. We show
results obtained for different values of speeds above the spiral critical speed.
The chosen values of the parameters are r = 10, V
T
= 1 and R
0
= 100.
V. COMPARATIVE ANALYSIS OF PINCER MOVEMENT
SEARCH STRATEGIES AND SAME-DIRECTION SWEEPS
The purpose of this section is to compare between the
obtained results for the circular and spiral same-direction
sweep processes that were developed in the previous sections
and compare them to pincer sweep processes developed in
[1]. In order to make a fair comparison between the total
sweep times of sweeper swarms that can perform both the
circular and spiral sweep processes the number of sweepers
and sweeper speed must be the same in each of the tested
spiral and circular swarms. The critical speed required for
sweepers that perform the same-direction circular or spiral
sweep processes is higher than the minimal critical speed
of their pincer sweep counterparts. Additionally, since pincer
sweep processes require a smaller critical speed compared
to same-direction sweep processes, in order to make a fair
comparison all sweepers in the swarm move at speeds above
the critical speed of 2 sweepers that perform the same-
direction circular sweep.
Fig. 7 shows the complete search times of swarms perform-
ing circular pincer sweeps, when the swarm’s sweepers move
at speeds above the same-direction circular critical speed. Fig.
8 shows the complete search times of swarms performing the
circular same-direction protocol. In both figures the sweepers
move at the same speeds above the same-direction circular
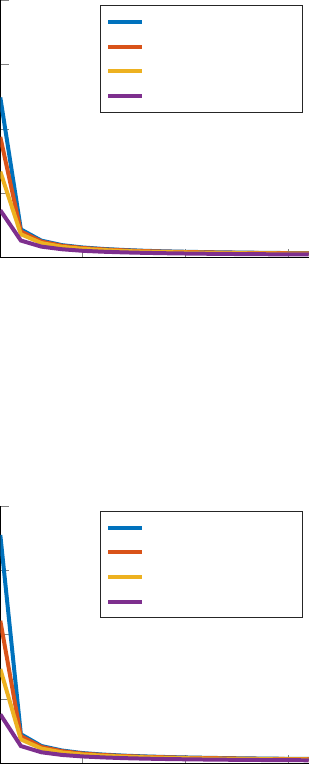
8
critical speed of 2 sweepers, since this speed is greater than
the critical speed of search processes performed with more
sweepers. We see that for all choices of speeds above the
same-direction circular critical speed of 2 sweepers, the ratio
between the complete search times of swarms performing
same-direction circular sweeps and swarms performing their
circular pincer sweep counterparts is greater than 1, implying
that same-direction circular sweeps require more time in order
to clean the entire evader region. Hence, from these results we
can conclude that performing circular pincer sweeps is always
better than performing same-direction circular sweeps.
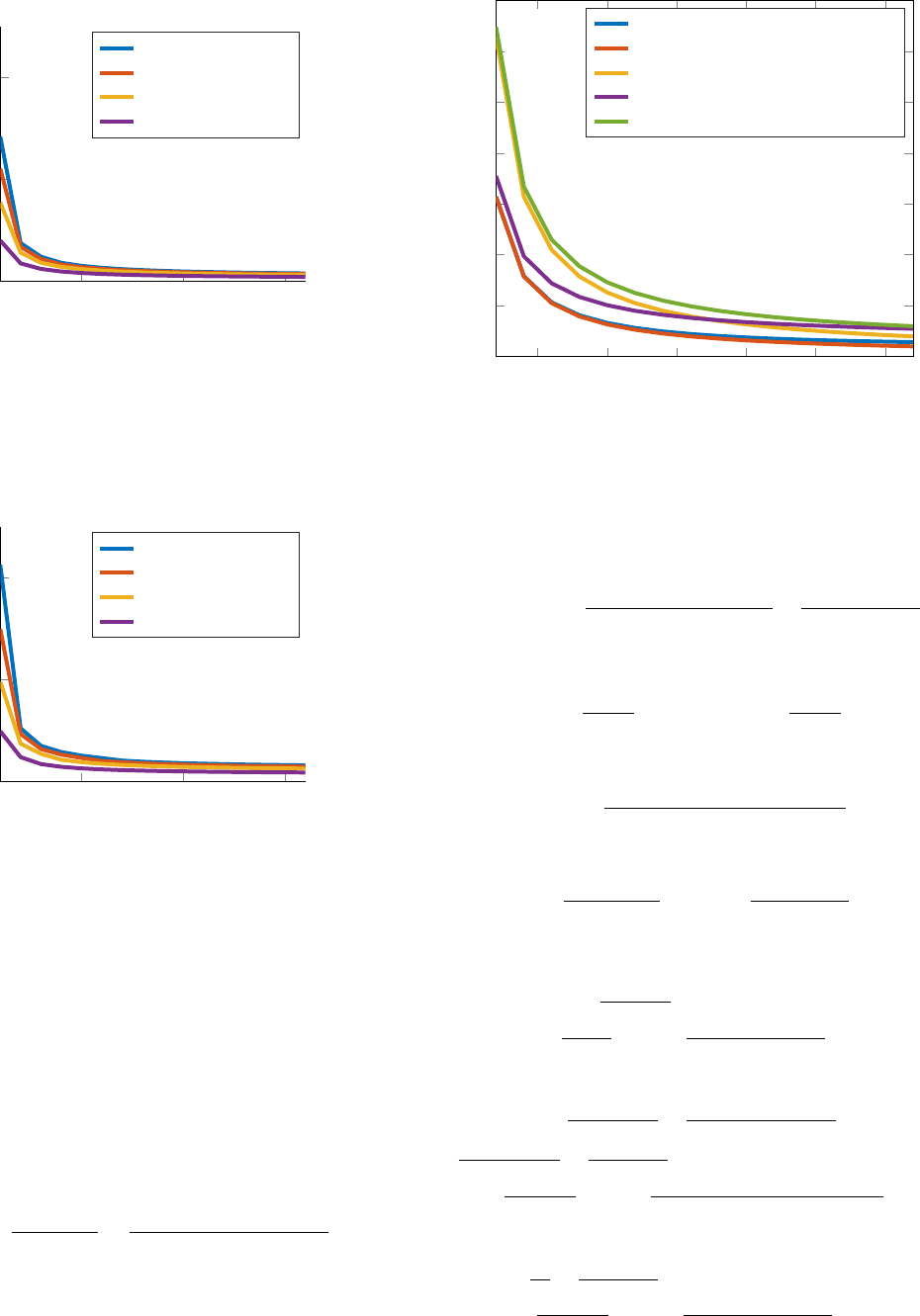
Fig. 9 shows the complete search times of swarms perform-
ing spiral pincer sweeps, when the swarm’s sweepers move at
speeds above the same-direction spiral critical speed. Fig. 10
shows the complete search times of swarms performing the
spiral same-direction protocol. In both figures the sweepers
move at the same speeds above the same-direction spiral
critical speed of 2 sweepers, since this speed is greater than
the critical speed of search processes performed with more
sweepers.
We see that for all choices of speeds above the same-
direction spiral critical speed of 2 sweepers, the ratio be-
tween the complete search times of swarms performing same-
direction spiral sweeps and swarms performing their spiral
pincer sweep processes counterparts is greater than 1, implying
that same-direction spiral sweeps require more time in order
to clean the entire evader region. This result is expected since
as the number of sweepers increases, the gain in utilizing
the cooperation between the sweeping pairs in pincer-based
sweep processes decreases the sweeping time more signifi-
cantly compared to sweepers that perform the same-direction
spiral sweeps. This occurs since same-direction sweepers must
sweep larger angular sections at each iteration in order to
ensure no evader escapes, while in pincer-based spiral search
strategies, sweeping these additional sections is unnecessary
due to the complementary trajectories of the sweepers.
Hence, from these results we can conclude that performing
spiral pincer sweeps is always better than performing same-
direction sweeps.
Fig. 11 presents a comparison between critical speeds
required to perform each sweep protocol. Requiring a higher
critical speed implies that there are entire regions of operation
where an evader region with a given radius could be cleaned
by a sweeper swarm that performs the same-direction spiral
sweep process but cannot be cleaned by a sweeper swarm
that performs the same-direction circular sweep process. This
also implies that swarms that perform pincer movement search
strategies can sweep larger regions than their same-direction
sweeps counterparts.
Furthermore, results show that as the number of sweepers
increases, circular pincer-based protocols require a smaller
critical speed even when compared to spiral same-direction
protocols. This result indicates that although implementing
pincer-based circular search protocols requires sweepers with
more basic capabilities compared to spiral protocols, the
cooperation between the sweepers considerably improves the
overall performance of the sweeper team.
10 20 30
0
100
200
300
400
Number of Agents
Time
Time of Complete Cleaning of the Evader Region-
Circular Pincer Sweep Processes
∆V =0.5V
T
- SD
∆V =2V
T
- SD
∆V =5V
T
- SD
∆V =15V
T
- SD
Fig. 7. This plot shows the obtained sweep times for sweeper swarms
performing the circular pincer sweep process that move at speeds above the
critical speed of the circular same-direction process. The chosen values of the
parameters are r = 10, V
T
= 1 and R
0
= 100.
10 20 30
0
100
200
300
400
Number of Agents
Time
Time of Complete Cleaning of the Evader Region-
Circular Same-Direction Sweep Processes
∆V =0.5V
T
- SD
∆V =2V
T
- SD
∆V =5V
T
- SD
∆V =15V
T
- SD
Fig. 8. This plot shows the obtained sweep times for sweeper swarms
performing the circular same-direction sweep process that move at speeds
above the critical speed of the same-direction circular process. The chosen
values of the parameters are r = 10, V
T
= 1 and R
0
= 100.
VI. CONCLUSIONS
This work compares same-direction sweeps and pincer
movement sweep protocols demonstrating and proving the
superiority of the latter. We perform a quantitative comparison
between pincer-based sweep protocols and same-direction
sweep protocols for any number of even sweepers where the
sensing capabilities and speeds of the swarms are equivalent.
We prove that critical speeds for pincer based search methods
are lower than their same-direction counterparts and therefore
allow to sweep successfully larger regions.
Afterwards, we provide a comparison between the different
search methods in terms of completion times of the sweep
processes and show that circular pincer-based approaches are
always better than their same-direction counterparts. Further-
9
10 20 30
0
100
200
Number of Agents
Time
Time of Complete Cleaning of the Evader Region-
Spiral Pincer Sweep Processes
∆ V =0.5V
T
- SD
∆ V =2V
T
- SD
∆ V =5V
T
- SD
∆ V =15V
T
- SD
Fig. 9. This plot shows the obtained sweep times for sweeper swarms
performing the spiral pincer sweep process that move at speeds above the
critical speed of the spiral same-direction process. The chosen values of the
parameters are r = 10, V
T
= 1 and R
0
= 100.
10 20 30
0
100
200
Number of Agents
Time
Time of Complete Cleaning of the Evader Region-
Spiral Same-Direction Sweep Processes
∆ V =0.5V
T
- SD
∆ V =2V
T
- SD
∆ V =5V
T
- SD
∆ V =15V
T
- SD
Fig. 10. This plot shows the obtained sweep times for sweeper swarms
performing the spiral pincer sweep process that move at speeds above the
critical speed of the spiral same-direction process. The chosen values of the
parameters are r = 10, V
T
= 1 and R
0
= 100.
more, we show that pincer-based spiral sweep search times
are shorter for all choices of search parameters compared to
their same-direction counterparts, as well.
Hence, for all choices of search parameters and protocols
the pincer-based protocols are best.
APPENDIX A
The inward advancement time at iteration i is denoted by
T
in
i
. It is given by,
T
in
i
=
δ
i
ef f
(∆V )
V
s
=
rn (V
s
− V
T
) − 2πR
i
V
T
nV
s
(V
s
+ V
T
)
(31)
The total advancement time until the evader region is bounded
by a circle of with a radius that is less than or equal to r is
5 10 15 20 25 30
0
5
10
15
20
25
30
35
Number of Agents
V
c
Critical Speeds for Confinement
Spiral Pincer Critical Speed
Optimal Minimal Critical Speed
Circular Pincer Critical Speed
Spiral SD Critical Speed
Circular SD Critical Speed
Fig. 11. Critical speeds as a function of the number of sweepers. The number
of sweepers is even, and ranges from 2 to 32 agents, that employ the spiral
and circular pincer sweep process and the same-direction sweep protocols.
The chosen values of the parameters are r = 10, V
T
= 1 and R
0
= 100.
denoted as
e
T
in
. It is given by,
e
T
in
=
N−2
X
i=0
T
in
i
=
(N
n
− 1) rn (V
s
− V
T
)
nV
s
(V
s
+ V
T
)
−
2πV
T
N
n
−2
P
i=0
R
i
nV
s
(V
s
+ V
T
)
(32)
We have that,
R
N
n
−2
=
c
1
1 − c
2
+ c
2
N
n
−2
R
0
−
c
1
1 − c
2
(33)
The sum of the radii is given by,
N
n
−2
X
i=0
R
i
=
R
0
− c
2
R
N
n
−2
+ (N
n
− 2)c
1
1 − c
2
(34)
Where the coefficients c
1
and c
2
are given by,
c
1
= −
r (V
s
− V
T
)
V
s
+ V
T
, c
2
= 1 +
2πV
T
n (V
s
+ V
T
)
(35)
Substitution of terms for the expression of R
N
n
−2
in (33)
yields,
R
N
n
−2
=
r(V
s
−V
T
)
2πV
T
+
1 +
2πV
T
V
s
+V
T
N
n
−2
2πR
0
V
T
−r(V
s
−V
T
)
2πV
T
(36)
Substitution of terms in (34) yields,
N
n
−2
P
i=0
R
i
= −
R
0
n(V
s
+V
T
)
2πV
T
+
rn
2
(V
s
−V
T
)(V
s
+V
T
)
(2πV
T
)
2
+
N
n
nr(V
s
−V
T
)
2πV
T
−
rn(V
s
−V
T
)
2πV
T
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
−1
(2πR
0
V
T
−rn(V
s
−V
T
))n(V
s
+V
T
)
(2πV
T
)
2
(37)
We therefore obtain that,
e
T
in
=
R
0
V
s
−
rn(V
s
−V
T
)
2πV
T
V
s
−
1 +
2πV
T
n(V
s
+V
T
)
N
n
−1
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
V
s
(38)

10
The last inward advancement is given by,
T
in
last
=
R
N
n
V
s
(39)
We have that,
R
N
n
=
c
1
1 − c
2
+ c
2
N
n
R
0
−
c
1
1 − c
2
(40)
Therefore,
R
N
n
=
rn(V
s
−V
T
)
2πV
T
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
(41)
Substitution of terms yields,
T
in
last
=
rn(V
s
−V
T
)
2πV
T
V
s
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
V
s
(42)
The total inward advancement times is therefore given by,
T
in
=
R
0
V
s
+
1 +
2πV
T
V
s
+ V
T
N−1
2πR
0
V
T
− r (V
s
− V
T
)
V
s
(V
s
+ V
T
)
(43)
The time it takes the sweepers to perform the circular sweeps
before the evader region is bounded by a circle with a radius
that is smaller or equal to r is given by,
e
T
circular
=
T
0
− c
2
T
N
n
−1
+ (N
n
− 1) c
3
1 − c
2
(44)
Where the coefficient c
3
is given by,
c
3
= −
2πr (V
s
− V
T
)
nV
s
(V
s
+ V
T
)
(45)
The time it takes the sweepers to perform the first sweep is
given by,
T
0
=
2πR
0
nV
s
(46)
The time it takes the sweepers to perform the last circular
sweep is given by,
T
N
n
−1
=
r(V
s
−V
T
)
V
s
V
T
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
−1
2πR
0
V
T
−rn(V
s
−V
T
)
nV
s
V
T
(47)
Therefore
e
T
circular
is given by,
e
T
circular
= −
R
0
(V
s
+V
T
)
V
s
V
T
+
r(V
s
−V
T
)(n(V
s
+V
T
)+2πV
T
N
n
)
2πV
T
2
V
s
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
(V
s
+ V
T
)
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
2
V
s
(48)
The last circular sweep occurs when the lowest tips of the
sweepers’ sensors are located at the center of the evader region.
It is given by,
T
last
=
2πr
nV
s
(49)
Therefore the total circular traversal times are given by,
T
circular
= −
R
0
(V
s
+V
T
)
V
s
V
T
+
r(V
s
−V
T
)(n(V
s
+V
T
)+2πV
T
N
n
)
2πV
T
2
V
s
+
1 +
2πV
T
n(V
s
+V
T
)
N
n
(V
s
+ V
T
)
2πR
0
V
T
−rn(V
s
−V
T
)
2πV
T
2
V
s
+
2πr
nV
s
(50)
APPENDIX B
For the one dimensional scan to be valid and ensure a non
escape search and complete cleaning of the evader region (7)
must be satisfied. This demand implies that,
2r − R
last
V
T
>
R
last
(3V
s
− V
T
)
(V
s
− V
T
)
2
(51)
By rearranging terms, (51) can be written as,
2r(V
s
− V
T
)
2
> R
last
V
s
(V
s
+ V
T
) (52)
By substitution of R
0
with αr where α > 1 and by substituting
the terms for V
s
and R
last
, (52) resolves to a quadratic
equation in ∆V that has only one positive root. This root
is a monotonically decreasing function in α, given by
∆V ≥
−4πV
T
α + πV
T
+ V
T
√
π
2
+ 8πn
2n
(53)
We have that,
2r(V
s
− V
T
)
2
> R
last
V
s
(V
s
+ V
T
) (54)
And,
V
s
=
2πR
0
V
T
rn
+ V
T
+ ∆V R
last
=
2πrV
T
nV
s
(55)
Denoting α =
R
0
r
and substituting the following terms in (54)
yields,
2r
2πV
T
α
n
+ ∆V
2
>
2πrV
T
n
2παV
T
n
+ 2V
T
+ ∆V
(56)
Rearranging terms yields a quadratic equation in ∆V ,
∆V
2
+ ∆V
4πV
T
α−πV
T
n
+
4π
2
V
T
2
α
2
−2π
2
αV
T
2
−2πnV
T
2
n
2
> 0
(57)
Equation (57) has a positive and a negative root. Since ∆V
is non-negative we are interested only in the positive root.
Therefore, in order to completely clean the evader region ∆V
has to satisfy
∆V ≥
−4πV
T
α + πV
T
+ V
T
√
π
2
+ 8πn
2n
(58)
APPENDIX C
In order for a linear scan to be applicable R
last
has to be
smaller than 2r. This leads to a requirement on the sweeper’s
velocity,
r
e
2πV
T
n
√
V
s
2
−V
T
2
− 1
< 2r (59)
Which resolves to,
e
2πV
T
n
√
V
s
2
−V
T
2
< 2 (60)
Yielding the requirement on the velocity,
V
s
> V
T
s
4π
2
(n ln 2)
2
+ 1 (61)
Since we previously observed that the spiral critical velocity
(for the considered spiral process) is close to the lower bound
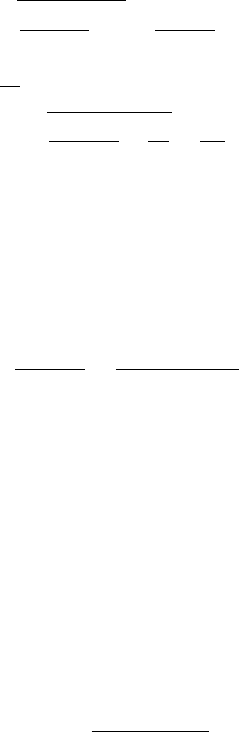
11
on the critical velocity, V
LB
, we can check whether the
condition in (59) is automatically satisfied. If the requirement
on V
s
in (61) is less than V
LB
, then since the sweepers move
with a velocity above it, then (59) is always satisfied. Therefore
if,
V
T
s
4π
2
(n ln 2)
2
+ 1 <
πR
0
V
T
nr
= V
LB
(62)
Or if the ratio
R
0
r
satisfies that,
s
4
(n ln 2)
2
+
1
π
2
<
R
0
r
(63)
Then R
last
is smaller than 2r.
APPENDIX D
For the one dimensional scan to be valid and ensure a non
escape search and complete cleaning of the evader region, (28)
must be satisfied. This demand implies that,
2r − R
f
V
T
>
R
f
(3V
s
− V
T
)
(V
s
− V
T
)
2
(64)
By rearranging terms, (64) can be written as,
2r(V
s
− V
T
)
2
> R
f
V
s
(V
s
+ V
T
) (65)
By substitution of R
0
with αr where α > 1 and by substi-
tuting the terms for V
s
and R
f
, (65) resolves to a quadratic
equation in ∆V that has only one positive root. This root is
a monotonically decreasing function in α, given by
V
s
2
(2r − R
f
) − V
s
V
T
(4r + R
f
) + 2rV
T
2
> 0 (66)
The quadratic equation in (66) has 2 positive roots. Therefore,
in order for the one dimensional linear scan to be valid V
s
has
to be greater than the largest positive root. Implying that,
V
s
≥
2rV
T
+ V
T
R
f
2r − R
f
(67)
REFERENCES
[1] R. Francos and A. M. Bruckstein, “Search for smart evaders with
swarms of sweeping agents,” IEEE transactions on robotics, doi:
10.1109/TRO.2021.3104253, pp. 1–20, 2021.
[2] B. O. Koopman, Search and screening: general principles with historical
applications. Pergamon Press, 1980.
[3] P. Vincent and I. Rubin, “A framework and analysis for cooperative
search using uav swarms,” in Proceedings of the 2004 ACM symposium
on Applied computing. ACM, 2004, pp. 79–86.
[4] Y. Altshuler, V. Yanovsky, I. A. Wagner, and A. M. Bruckstein, “Efficient
cooperative search of smart targets using uav swarms,” Robotica, vol. 26,
no. 4, pp. 551–557, 2008.
[5] A. Bressan, M. Burago, A. Friend, and J. Jou, “Blocking strategies for
a fire control problem,” Analysis and Applications, vol. 6, no. 03, pp.
229–246, 2008.
[6] A. Bressan and T. Wang, “On the optimal strategy for an isotropic block-
ing problem,” Calculus of Variations and partial differential equations,
vol. 45, no. 1-2, pp. 125–145, 2012.
[7] Z. Tang and U. Ozguner, “On non-escape search for a moving target by
multiple mobile sensor agents,” in 2006 American Control Conference.
IEEE, 2006, pp. 6–pp.
[8] T. G. McGee and J. K. Hedrick, “Guaranteed strategies to search for
mobile evaders in the plane,” in 2006 American Control Conference.
IEEE, 2006, pp. 6–pp.
[9] P. C. Hew, “Linear and concentric arc patrols against smart evaders,”
Military Operations Research, vol. 20, no. 3, pp. 39–48, 2015.
[10] J. F. Fisac, M. Chen, C. J. Tomlin, and S. S. Sastry, “Reach-avoid
problems with time-varying dynamics, targets and constraints,” in
Proceedings of the 18th international conference on hybrid systems:
computation and control, 2015, pp. 11–20.
[11] M. Chen, Z. Zhou, and C. J. Tomlin, “Multiplayer reach-avoid games via
pairwise outcomes,” IEEE Transactions on Automatic Control, vol. 62,
no. 3, pp. 1451–1457, 2016.
[12] D. Shishika and V. Kumar, “Local-game decomposition for multiplayer
perimeter-defense problem,” in 2018 IEEE Conference on Decision and
Control (CDC). IEEE, 2018, pp. 2093–2100.
[13] D. Shishika, J. Paulos, and V. Kumar, “Cooperative team strategies for
multi-player perimeter-defense games,” IEEE Robotics and Automation
Letters, vol. 5, no. 2, pp. 2738–2745, 2020.
[14] V. R. Makkapati and P. Tsiotras, “Optimal evading strategies and task
allocation in multi-player pursuit–evasion problems,” Dynamic Games
and Applications, vol. 9, no. 4, pp. 1168–1187, 2019.
[15] R. M. Francos and A. M. Bruckstein, “Search for smart evaders with
sweeping agents,” Robotica, vol. 39, no. 12, pp. 2210–2245, 2021.
[16] T. H. Chung, G. A. Hollinger, and V. Isler, “Search and pursuit-evasion
in mobile robotics,” Autonomous robots, vol. 31, no. 4, pp. 299–316,
2011.
[17] S. S. Kumkov, S. Le M
´
enec, and V. S. Patsko, “Zero-sum pursuit-evasion
differential games with many objects: survey of publications,” Dynamic
games and applications, vol. 7, no. 4, pp. 609–633, 2017.
[18] I. E. Weintraub, M. Pachter, and E. Garcia, “An introduction to pursuit-
evasion differential games,” in 2020 American Control Conference
(ACC). IEEE, 2020, pp. 1049–1066.
