Guaranteed Evader Detection in Multi-Agent Search Tasks using

Guaranteed Evader Detection in Multi-Agent Search

Tasks using Pincer Trajectories

Roee M. Francos and Alfred M. Bruckstein

Abstract—Assume that inside an initial planar area there

are smart mobile evaders attempting to avoid detection by a

team of sweeping searching agents. All sweepers detect evaders

with fan-shaped sensors, modeling the ﬁeld of view of real

cameras. Detection of all evaders is guaranteed with cooperative

sweeping strategies, by setting requirements on sweepers’ speed,

and by carefully designing their trajectories. Assume the smart

evaders have an upper limit on their speed which is a-priori

known to the sweeping team. An easier task for the team of

sweepers is to conﬁne evaders to the domain in which they are

initially located. The sweepers accomplish the conﬁnement task

if they move sufﬁciently fast and detect evaders by applying an

appropriate search strategy. Any given search strategy results

in a minimal sweeper’s speed in order to be able to detect all

evaders. The minimal speed guarantees the ability of the sweeping

team to conﬁne evaders to their original domain, and if the

sweepers move faster they are able to detect all evaders that

are present in the region. We present results on the total search

time for a novel pincer-movement based search protocol that

utilizes complementary trajectories along with adaptive sensor

geometries for any even number of pursuers.

I. INTRODUCTION

Motivation. The goal of this research is to provide efﬁ-

cient “must-win” search strategies for a team of n identical

sweeping agents that must guarantee detection of an unknown

number of smart evaders that are initially located inside a given

circular region of radius R

while minimizing the search time.

The evaders move and try to escape the initial region and have

maximal speed of V

, known to the sweepers, and do not have

any turning constraints.

A smart evader is one that detects and responds to the

motions of searchers by performing optimal evasive maneu-

vers, to avoid interception. A smart evader is assumed to have

full knowledge of the search strategy of the sweeping team.

Possessing such knowledge enables smart evaders to plan their

movements in a way that maximizes the time required for

the pursuing sweepers to detect them. Guaranteed detection

of all evaders implies that for all particular choices of escape

strategies smart evaders may implement in response to the

motions of searches, they will all eventually be detected.

Agents gather information only from their sensors, and

evaders in a sweeper’s ﬁeld of view are immediately detected.

There can be many evaders, and those can be located at any

point in the interior of the circular region at the beginning

of the search process. Importantly, in contradiction to most

recent literature on pursuit-evasion problems, the sweepers do

not have any information regarding evaders locations’ that

are outside of their sensing range, nor on the total number

of evaders they must detect. All sweepers move at a speed

> V

(measured at the center of the sensor that represents a

sweeper’s center of mass) and detect evaders using fan shaped

sensors with a given half-angle denoted by α and a length of

2r. Finding an efﬁcient algorithm requires that, throughout

the sweep, the footprint of the sweepers’ sensors maximally

overlaps the evader region (the region where evaders may

possibly be) in order to detect as many evaders as possible.

The sweeping team consists of an even number of agents,

referred to as sweepers, that act as sensors and sweep the

region until all evaders are detected. The search is done by

pairs of agents sweeping toward each other for the purpose

of entrapping all evaders. Cooperation among agents scanning

adjacent sectors and sweep toward each other enables them to

entrap all evaders, regardless of evaders’ adversarial motions.

Since the sweepers do not have any additional knowledge

about the evaders whereabouts, or even if all evaders were

found at some intermediate point of time during the search,

the search is continued until the whole region is searched.

Additional information such as the number of evaders and

their exact locations provided to the sweeper team in advance,

could reduce the termination time by utilizing this knowledge

and organizing the entire search process differently. However

this is not the focus of this paper. Therefore, the resulting

search times for a circular environment can be seen as an

upper bound on the search time, resulting from the lack of

speciﬁc information about evaders locations.

We chose to analyze the performance of the system with

a fan-shaped sensor as this type of sensor is highly common

in many sensing and scanning applications, from optical to

radar and sonar. Fan-shaped sensors with a variable half-

angle resemble actual pinhole camera visual sensors of a given

aperture. Furthermore, a fan shaped sensor with a larger area

can reduce the critical speed and sweep time compared to

approaches that use linear sensors while avoiding the usage of

unrealistic sensors such as circular sensors which assume to

detect evaders in all angles around a searcher.

The considered protocol may be implemented in a 2D

environment in which the actual agents travel on a plane or

as a 3 dimensional search where the sweepers are drone-like

agents which ﬂy over the evader area at different heights.

Guaranteed evader detection in practical robotic ap-

plications. A wide range of real-world tasks that are nowa-

days carried out by human-controlled machines are expected

to be replaced by partially autonomously operated robots

in the nearby future. Search and rescue missions, airborne

surveillance applications, various monitoring tasks for secu-

rity applications, wildlife tracking, ﬁre control as well as

arXiv:2305.00533v1 [cs.MA] 30 Apr 2023

inspection tasks in hazardous zones can all beneﬁt from the

theoretical and experimental results developed in this work.

The combination of the proposed search protocol and sensor

choice enables nearly optimal cooperation between agents and

allows the deployment of multi-robot teams with superior

performance.

For the mentioned applications, guaranteeing success in the

worst-case scenario ensures succeeding in the task for all other

simpler scenarios as well. This approach is often used in real-

world settings where full state information is not available and

performance guarantees must be kept.

The searching agents considered in this work do not assume

knowledge of the number of evaders present in the region,

their locations, or their escape plan and despite that they are

able to detect all of them. Therefore, this work is of prime

theoretical and practical importance as is in many pursuit-

evasion games the searching team does not have complete

information about its opposing team, as is often assumed by

many previous papers.

Since multi-agent pursuit-evasion search protocols mainly

utilize multi-agent UAVs, sweepers ﬂy over the environment

containing the evaders, therefore investigating issues such as

obstacles is not the main focus of the work, because the

sweeping team ﬂies over them. Obstacles limit the movements

and locations of ground-moving evaders, and therefore their

presence assists the searching team to detect them since it

limits the escape options of evaders, and thus does not impact

our “worst-case” analysis.

The mentioned protocols can use a vast suite of onboard

sensors to detect evaders, depending on the domain of ap-

plication. Potential choices vary from visual sensors such as

cameras which have the beneﬁt of having a high resolution and

being lightweight. Therefore, detecting evaders with cameras

requires a smaller battery in order to accomplish the desired

task compared to other sensing modalities such as radars that

increase the weight of the payload and hence limit the duration

of the search mission due to increased energy consumption.

Actual detection of evaders can utilize a vast number of

computer-vision detection algorithms such as [1], [2].

Since to our use case, the preferred choice for the detection

modality is a camera, we extend and generalize previous works

on guaranteed detection of smart targets to accommodate

usage of such sensors. Previous works such as used circular

sensors and linear sensors. However, since both circular and

linear sensors offer simplistic assumptions about the area

detected by actual searching robot teams, in this work we

extend and generalize state-of-the art results on guaranteed

detection of smart evaders that use pincer sweeps between

searching pairs to search teams that use sensors modelling

actual visual detectors. Our obtained results are insensitive to

locations of evaders or their numbers. The proposed protocols

can be applied in other convex environments as well, by using

slight modiﬁcations to the explored sweeping strategies.

Overview of related research. Several interesting search

problems originated in the second world war due to the need

to design patrol strategies for aircraft aiming to detect ships

or submarines in the English channel, see [3]. Patrolling a

corridor with multi agent teams whose goal is ensuring detec-

tion and interception of smart evaders was also investigated in

[4] while optimally proven strategies were provided in [5]. A

somewhat related, discrete version of the problem, was also

investigated in [6]. It focuses on a dynamic variant of the

cooperative cleaners problem, a problem that requires several

simple agents to a clean a connected region on a grid with

contaminated pixels. This contamination is assumed to spread

to neighbors at a given rate.

In [7], [8], Bressan et al. investigate optimal strategies for

the construction of barriers in real-time aiming at containing

and conﬁning the spread of ﬁre from a given initial area of

the plane. The authors are interested in determining a minimal

possible barrier construction speed that enables the conﬁne-

ment of the ﬁre, and on determining optimality conditions for

conﬁnement strategies.

A non-escape search procedure for evaders that are origi-

nally located in a convex region of the plane from which they

may move out of, is investigated in [9], and a cooperative

progressing spiral-in algorithm performed by several agents

with disk shaped sensors in a leader-follower formation is

proposed. In [10], McGee et al. investigate guaranteed search

patterns for smart evaders that do not have any maneuverability

restrictions except for an upper limit on their speed. The sensor

the agents are equipped with detects evaders within a disk

shaped area around the searcher’s location. Search patterns

consisting of spiral and linear sections are considered. In [11],

Hew investigates search for smart evaders by implementing

concentric arc trajectories with agents having disk-shaped

sensors similar to the ones used in [10]. The aim of search

protocol is to detect submarines in a channel or in a half plane.

Another set of related problems are pursuit-evasion games,

where the pursuers’ objective is to detect evaders and the

evaders objective is to avoid the pursuers. Pursuit-evasion

games include combinations of single and multiple evaders

and pursuers scenarios. These types of problems are addressed

in the context of perimeter defense games by Shishika et al.

in [12], [13], with a focus on utilizing cooperation between

pursuers to improve the defense strategy. In [12], implicit

cooperation between pairs of defenders that move in a “pincer

movement” is performed to intercept intruders before they

enter a planar convex region. In [14], pursuit–evasion problems

involving multiple pursuers and multiple evaders (MPME) are

studied. The original MPME problem is decomposed to a

sequence of simpler multiple pursuers single evader (MPSE)

problems by classifying if a pursuer is relevant or redundant

for each evader and only the relevant pursuers participate in

the MPSE pursuit of each evader. Pursuers and evaders are all

assumed to be identical, and pursuers follow either a constant

bearing or a pure pursuit strategy. The problem is simpliﬁed

by adopting a dynamic divide and conquer approach, where at

every time instant each evader is assigned to a set of pursuers

based on the instantaneous positions of all the players. The

original MPME problem is decomposed to a sequence of

simpler multiple pursuers single evader (MPSE) problems by

classifying if a pursuer is relevant or redundant for each

evader by using Apollonius circles. Only the relevant pursuers

participate in the MPSE pursuit of each evader.

Recent surveys on pursuit evasion problems are [15]–[17].

In [15], a taxonomy of search problems is presented. The

paper highlights algorithms and results arising from different

assumptions on searchers, evaders and environments and dis-

cusses potential ﬁeld applications for these approaches. The

authors focus on a number of pursuit-evasion games that are

directly connected to robotics and not on differential games

which are the focus of the other cited surveys. [16] presents

a survey on pursuit problems with 1 pursuer versus 2 evaders

or 2 pursuers versus 1 evader are formulated as a dynamic

game and solved with general methods of zero-sum differential

games. In [17], the authors present a recent survey on pursuit-

evasion differential games and classify the papers according

to the numbers of participating players: single-pursuer single-

evader (SPSE), MPSE, one- pursuer multiple-evaders (SPME)

and MPME. In [18], a two-player differential game in which a

pursuer aims to capture an evader before it escapes a circular

region is investigated. In [19], the problem of border defense

differential game where M pursuers cooperate in order to

optimally catch N evaders before they reach the border of

the region and escape is investigated.

Contributions: We present a comprehensive theoretical and

numerical analysis of trajectories, critical speeds and search

times for a team of n cooperative sweeping agents equipped

with fan-shaped sensors with a variable half-angle, whose

mission is to guarantee detection of all smart evaders that are

initially located inside a given circular region from which they

may move out of to escape the pursuing sweeping agents.

• We present a novel pincer search strategy utilizing pincer

sweeps and complementing sensor geometries to improve

the detection capabilities of the search team.

• We develop analytic formulas for a search protocol, ap-

plicable to any even number of sweepers with fan-shaped

sensors with a given half-angle. Fan shaped sensors with

a variable half-angle that model the actual ﬁeld-of-view

of visual sensors, therefore enabling the applicability of

the established results in real-world search scenarios.

• We extend state-of-the-art multi-pursuer multi-evader lit-

erature to scenarios with arbitrary large numbers of

evaders, where very limited information is available to the

pursuers, and even so they are able to optimally cooperate

in order to successfully complete their mission.

The research performed in this paper extends and gener-

alizes previous results on linear and circular sensors such as

[10], [20] to fan-shaped sensors with an arbitrary angle. Since

“at the limit”, a linear shaped sensor is a special case of a fan

shaped sensor with an angle of 0 and circular or disk-shaped

sensors are fan shaped sensors with an angle of 2π.

Hence the analysis performed in this work provides a signif-

icant theoretical milestone in generalizing previous results and

allowing the application of the established results to practical

robotic vision-based search tasks.

Numerical Evaluation. The theoretical analysis is comple-

mented by simulation experiments in MATLAB and NetLogo

that verify the theoretical results, highlight the performance of

search strategies with different number of sweepers and sen-

sors and illustrates them graphically in the ﬁgures embedded

throughout the text and in the accompanying video.

Paper Organization. The paper is organized as follows:

Section 2 describes the motivation and setting for using pincer-

based search strategies. Section 3 presents a optimal lower

bound on the sweepers’ speed that is independent of the spe-

ciﬁc chosen sweep protocol. In section 4, an analytical analysis

of critical speeds and sweep time is provided, accompanied by

numerical results. In the last section conclusions are given and

future research directions are discussed.

II. PINCER-BASED SEARCH PROBLEM FORMULATION

Inherently, the complete search time of the region depends

on the sweeping protocol the sweeping team implements.

The protocols we propose aim to reduce the radius of the

circle bounding the evader region after each full sweep. This

guarantees complete elimination of the potential area where

evaders may be located.

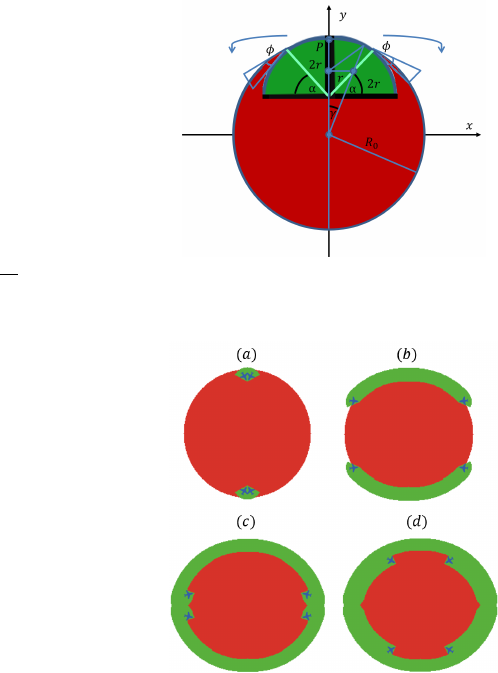
At the beginning of the search, we assume the entire area of

the sweepers’ sensors is inside the evader region. This implies

that the full length of the central line of the sweepers’ sensors

(see the light green lines that depicts this part of the sensor in

Fig. 1) is inside the evader region, i.e., a footprint of length 2r.

The sweepers’ sensors are shown in green in Fig. 1 as well.

The blue circle on the light green line depicts the center of the

sensor of clockwise sweeping agent (and therefore its center

of mass). α denotes the half-angle of the sweepers fan-shaped

sensors.

If we were to distribute sweepers equally along the bound-

ary of the initial evader region, and have them move in the

same direction, potential escape from the points adjacent to

the starting locations of the sweepers might occur. To enable

sweepers to succeed in the task while having the lowest

possible critical speed, we propose that pairs of sweepers

move out in opposite directions along the boundary of the

evader region and sweep in a pincer movement instead of

implementing a protocol where all sweepers move in the same

direction along the boundary.

The proposed strategy can be applied with any even number

of sweepers. Each sweeper is responsible for an angular sector

of the evader region that is proportional to the number of

sweepers. The sweepers’ ﬁeld-of-views are initially positioned

in pairs back-to-back. One sweeper in the pair moves counter-

clockwise while the other sweeper in the pair moves clock-

wise. Once the sweepers meet, i.e. their sensors are again

superimposed at a meeting point, they switch the directions

in which they move. Changing of directions takes place every

time sweepers “bump” into each other.

It is worth emphasizing that once a sweeper leaves a location

that was cleared from evaders, other evaders may attempt

to reach this location again. Therefore, the proposed sweep

protocol must ensure that there is no evaders strategy that

enables any evader to escape even if evaders wait at the edge

of a cleared location and start their escape instantly after a

sweeper leaves this location.

Sweepers implementing pincer movements solve the prob-

lem of evader region’s spread from the ”most dangerous

points”. Evaders located at these points have the maximum

time to escape throughout the sweepers’ movements. Conse-

quently, if evaders attempting to escape from these locations

are detected, evaders attempting to escape from all other

locations are detected as well. When a pair of sweepers

travelling in a pincer movement ﬁnishes sweeping its allocated

section of the environment (particularly an angle of

2π

− γ,

which is explained in detail in the next section), provided they

move at a speed exceeding the critical speed, the spread of the

evader region that originates from these points has to be less

than 2r. Therefore, the sweepers advance towards the center

of the evader region by the margin between the spread of the

evader region during this motion and 2r.

Since a pair of sweepers begin their sweep when the foot-

prints of their sensors are “back-to-back”, the evader region’s

points that should be considered to guarantee detection of all

evaders are located at the inner tips of the central part of the

sweepers’ sensors closest to the center of the evader region

and not from points on the boundary of the evader region.

If all sweepers move in the same direction following

their equally spaced placement around the region, the evader

region’s points that need to be considered for limiting the

region’s spread are points located on the boundary of the

evader region. This will in turn result in higher critical speeds

for sweepers implementing same-direction sweeps. Requiring

higher critical speeds also results in longer sweep times for

same-direction protocols compared to pincer based methods.

In [21], a quantitative analysis comparing critical speeds and

sweep times between pincer-based search protocols and same-

direction protocols operated by the same teams of sweepers

is investigated for agents with different sensors and sweep

protocols then the ones considered in this work. The analysis

in [21] indicates that the critical speeds and sweep times

for agents employing same direction sweeps is indeed higher

compared to the pincer-based speeds. We assume this applies

in this settings as well and plan to analytically compare these

search methodologies in future work.

The proposed search pattern uses spiral scans, related to

the sweep pattern suggested in [10]. In order to have maximal

sensor footprint intersecting the evader region throughout the

sweep, the proposed search pattern aims to track the expanding

evader region’s “wavefront”.

Simulations demonstrating the evolution of the search strate-

gies are generated using NetLogo software [22] and shown in

Fig. 2. Green areas are locations that are free from evaders and

red areas indicate locations where potential evaders may still

be located. Fig. 2 shows the cleaning progress of the evader

region when 4 sweepers employ the proposed sweep protocol.

Comparison to related research. In [23], the conﬁnement

and complete detection tasks for a line formation of agents

or alternatively for a single agent with a linear sensor are

Fig. 1. Initial placement of 2 sweepers employing the spiral pincer sweep

strategy.

Fig. 2. Swept areas and evader region status for different times in a scenario

where 4 agents employ the spiral pincer sweep process and α = 30

◦

. (a)-

shows the status at beginning of ﬁrst cycle, (b)- shows the status midway

through the ﬁrst cycle, (c)-shows the status at beginning of the second cycle

and (d) shows the status toward the end of the second cycle.

analyzed. The presented approach ensures detection of all

evaders, however the complete detection time and the critical

speeds required for the sweeping formation to succeed in

its task are inferior to the results achieved in this work,

since no pincer sweeps are performed and since the line

formation performs simple circular motion and does not track

the expanding wavefront of potential evader locations as is

performed in this work. In [20], teams of agents perform pincer

sweep search strategies with linear sensors. These two early

works assume linear sensors and not fan-shaped sensors as the

ones assumed in this paper, hence this paper can be regarded as

a generalization of the results from [20] to fan-shaped sensors

with a given half-angle that model the ﬁeld-of-view of actual

cameras allowing applicability of the results to real robotic

search and surveillance missions.

While automated discovery of search policies relies on

knowledge of the players’ locations throughout the search

process (as assumed in [12], [13]), to plan the trajectories

of pursuers and evaders, in our setting we bypass the need

for such extensive and often unrealistic knowledge of the

environment and perfect communication exchange between

members of the same team with a simple and efﬁcient strategy.

Furthermore, in contrast to [12], [13] we do not assume a ﬁnite

number of evaders and that each sweeper can intercept only a

single evader, and guarantee interception of all evaders.

As opposed to our work, references [10], [11] use a disk

shaped sensor with a radius of r, and do not calculate

the detection times of all evaders. Although the works in

references [12], [13] use pincer movements between pairs of

defenders as well, they have a different objective of protecting

an initial region from invaders, contrary to our goal which is

to detect all evaders that may spread from the interior of the

region. Furthermore these works are concerned with devising

policies for intercepting as many intruders as possible relying

on an assumption that the number of intruders is ﬁnite and

that each defender can only intercept a single intruder and not

on guaranteeing interception of all evaders or intruders, as is

the aim of our work.

Contrary to the work reported in references [18], [19], we

do not assume the number of evaders is known to the pursuers

and not that the members of each party have full access to the

locations of the members of the opposing party and use it

in order to plan their actions. From our point of view using

such information is unrealistic for search applications where

determining the locations of the opposing team members

is at the heart of the problem. Such knowledge requires

very sophisticated sensing capabilities when searching large

regions. Furthermore, we solve the assignment of pursuers to

evaders elegantly by assigning sweeper pairs based on their

geometric location. This simple assignment rule alleviates the

need for communicating synchronized and precise location

information between the searchers.

III. LOWER BOUND ON THE SPEED OF SWEEPERS WITH

FAN-SHAPED SENSORS

We present an optimal bound on the speed of sweepers

equipped with fan shaped sensors. The developed bound

is irrespective of the choice of the implemented sweeping

protocol. This bound serves as one of the benchmarks that are

used to compare the performance of different search strategies

by a metric we refer to as the critical speed.

The largest number of evaders are detected when the entire

fan shaped sensor overlaps the evader region. For a fan shaped

sensor of length 2r and half angle α the maximal rate of

detecting evaders must be higher than the minimal expansion

rate of the evader region. Else, there is no feasible sweeping

protocol that can ensure the detection of all evaders.

The lower bound is derived for a sweeper team containing n

identical sweepers. The smallest sweeper’s speed that ensures

the maximal detection rate is larger than the minimal expan-

sion rate is based purely on geometric properties of the evader

region, the sweepers sensors’ dimensions and the evaders’

maximal speed. This lower bound on the speed is deﬁned as

the critical speed and is denoted by V

πR

(1)

This lower bound is similar for line sensors and its proof

follows the derivation such a lower bound for a sweeper’s

critical speed in [20]. Similar results for the bound in [20] for

sweepers with circular sensors are given in [10].

If sweepers move at speeds that exceed the critical speed,

they possess the ability to implement a suitable sweep protocol

that decreases the evader region, therefore allowing them to

sweep the next iteration around a smaller region. Therefore,

the critical speed is calculated based on the sweep around

the initial and largest radius, since sweeping around smaller

regions takes less time. Therefore, if the sweepers succeeded

in conﬁning evaders to the larger and initial evader region

they will surely succeed when the evader region decreases

throughout the search protocol (since their speed stays constant

throughout the protocol).

IV. SPIRAL PINCER SWEEP STRATEGIES FOR SWEEPERS

WITH FAN-SHAPED SENSORS

A. The Critical Speed

In order for the sweeper team to efﬁciently scan the region,

we desire that there will be maximal intersection between

the sweepers’ sensors and the evader region. Implementing

spiral trajectories, in which sweepers’ sensors track the ex-

panding evader region’s wavefront, allows the sweeping team

to achieve nearly optimal efﬁciency as proven in this section.

We consider a scenario in which a sweeping team consisting

of n sweepers, where n is even. All sweepers have fan-shaped

sensors with ﬁnite visibility that model the sensor geometry of

real cameras. Sweepers’ sensors have a diameter length of 2r

and a half-angle of α, as shown in Fig. 1. Selecting sweepers

with complementing sensor geometries along with having the

sweepers move in opposite directions prevents evaders from

devising an escape strategy that leverages the gap between the

sweepers’ sensors, since the ﬁeld-of-views of each sweeping

pair are tangent to each other. These considerations highlight

the beneﬁts of using both pincer sweeps along with sensor

geometries between sweeping pairs that complete each other

in order to achieve maximal evader detection performance.

Fig. 1 shows the initial setting of the problem when 2 sweep-

ers perform the search. The symmetry between the trajectories

of adjacent searching pairs prevents potential escape of evaders

from point P = (0, R

), ”the most dangerous point“ evaders

may attempt to escape from due to similar consideration as

are proven in [23].

Hence, a sweeper’s critical speed depends solely on the time

required for it to sweep its allocated angular sector. Deﬁne by

γ the angle describing the offset angle of the center of the

sweeper from the center of the region at the beginning of the

sweep process, see Fig. 1 for a geometric illustration of γ.

The relation between γ and α obtained by using the law of

cosines on the depicted triangles of Fig. 1 and is given by,

= R

+(R

− 2r + r cos α)

−2R

− 2r + r cos α) cos γ

(2)

Rearranging terms yields,

γ = arccos



+2R

r(cos α−2)+r

cos α(cos α−2)

+r cos α−2r)



(3)

Therefore, at each sweep agents traverse an angle of

2π

− γ.

After sweepers complete searching their allocated sector, and

only if they move at a sufﬁcient speed, they advance toward

the center of the evader region together. If the search is planar,

sweepers switch the sweeping directions following an inward

movement toward the center. If the search is 3 dimensional,

sweepers ﬁrst move together toward the center of the region

and only afterwards exchange the sector they sweep with

the sweeping teammate they perform the pincer sweep with.

Following this motion they commence sweeping an evader

region bounded by a circle with a smaller radius.

Sweepers begin their spiral motion with the outer tip of the

central line of their fan-shaped sensor tangent to the evader

region’s boundary. To preserve the outer central tip of their

sensor tangent to the evader region, sweepers move with an

angular offset of φ to the normal of the evader region (at

each point) throughout their sweep. φ is the angle between

the outer tip of the central line of a sweeper’s sensor and the

normal of the evader region at the meeting point between the

evader region and the tip of the central line of the sensor that

is furthest from the center of the evader region (see the light

green line that depicts this part of the sensor in Fig. 1). φ

depends on the ratio between the sweeper and evader speeds

(see Fig. 1 for its depiction). The sweepers’ incentive to move

at a constant angle φ to the normal of the evader region is

to preserve the evader region’s circular shape and to keep as

much of their sensor footprint inside the evader region at all

times in order to detect a maximal number of evaders. φ is

given by,

sin φ =

(4)

Because spiral sweeping preserves the evader region’s cir-

cular shape, as a result of the isoperimeteric inequality such

trajectories necessitate that the length of the curve bounding

the evader region is minimal and therefore the time required

for the sweepers to sweep around it is minimal as well. Denote

by θ

the sweeper’s angular speed, given by,

dθ

cos φ

(t)

− V

(t)

(5)

Integration of (5) with the initial and ﬁnal sweep times of the

angular sector as the integral’s limits is,

θ (ζ)dζ =

− V

ζ + R

− r

dζ (6)

With a solution for θ (t

) obtained from (6) given by,

θ (t

) =

− V



+ R

− r



(7)

Raising by an exponent (7) yields,

− r) exp

θ(t

)

− V

= V

+ R

− r = R

)

(8)

The time required for a sweeper to scan its allocated angular

section corresponds to it sweeping an angle of θ by

2π

− γ

around the region. While the sweeper performs this motion, the

evader region’s expansion must be at most 2r from its initial

radius. Otherwise, the sweepers will not be to detect potential

evaders attempting to escape from the region. Allowing a

spread of at most 2r is a simpliﬁcation of the problem that

assumes that while the sweepers progress toward the center

of the evader region the evaders do not spread. Obviously this

is not a realistic assumption, hence we address this case after

the solution of the simpliﬁed setting. To guarantee that no

potential evader escapes the sweepers, following a sweep by

2π

− γ we must demand that,

+ r ≥ R

2π

−γ

) (9)

Deﬁne,

∆

= exp

(

2π

− γ)V

− V

(10)

Replacing R

2π

−γ

) with the expression derived for the tra-

jectory of the sweeper’s center results in, R

+r ≥ (R

− r) λ.

Hence, to guarantee no potential evader escapes without being

detected by the sweeper team, it is mandatory for the sweep-

ers’ speed to exceed,

≥ V



2π

− γ





−r



+ 1 (11)

As mentioned earlier, in order to accommodate the ex-

pansion of evaders during the inward motion of sweepers

a modiﬁcation to the critical speed in (11) must be made.

This change requires that when sweepers move inwards after

they ﬁnish their sweep, they must meet the evader region’s

expanding wavefront that moves outwards from every point

in the evader region with a speed of V

at the previous

radius R

. Incorporating this constraint into the solution of

the critical speed guarantees that no evaders escape during the

sweepers inwards motion as well. Denote by T

the evader

region’s expansion throughout the ﬁrst sweep. In order for no

evader to escape detection the following inequality must hold,

≤

2rV

. Replacing T

with

−r)(λ−1)

results in,

− r) (λ − 1) =

2rV

+ V

(12)

Theorem 1. For a spiral pincer sweep protocol with n

sweepers in which n is even, the critical speed , V

, that allows

the sweeping team to conﬁne all evaders to their original

domain is computed from,

= V

1 −

−r)(λ−1)

(13)

The solution for the critical speed is calculated numerically

by applying the Newton–Raphson method. The simpliﬁed

critical speed of (11) serves as an initial guess. In the rest of

the article the critical speed considered is that of theorem 3,

thus it accounts for the expansion of the evader region during

the sweepers advancements into the center of the region.

B. Analytical Sweep Time Analysis

Theorem 2. For a team of n sweepers implementing the pincer

sweep protocol, the time required to detect all evaders in the

region and reduce the evader region’s area to 0 is given by the

sum of inward advancement times after all the sweeps,T

(n),

along with the sum of all the spiral traversal times, T

spiral

(n)

in all sweeps. Hence,

T (n) = T

(n) + T

spiral

(n) (14)

Proof. Denote by ∆V > 0 the excess speed of a sweeper

above the critical speed. The sweeper’s speed hence is V

+∆V . Let θ (t

) denote the angle of a sweeper with respect

to the center of evader region. At the start of each sweep the

center of a sweeper’s sensor is located at a distance of R

− r

from the center of the evader region. θ (t

) is calculated in

(7). Replacing R

with R

yields,

θ (t

) =

− V



+ R

− r



(15)

Denote by T

spiral

the time required for a sweeper to sweep

an angle of θ (t

) =

2π

− γ

. This time can be calculated by

rearranging terms in (15) and equals,

spiral

− r) (λ − 1)

(16)

In case sweepers move at speeds exceeding the critical speed

appropriate for the scenario, denote the distance every sweeper

advances toward the center of the evader region by δ

(∆V ).

Following this inward motion, the evader region decreases and

is contained inside a smaller circular evader region having a

radius of R

i+1

= R

− δ

(∆V ). Hence δ

(∆V ) equals,

(∆V ) = 2r − V

spiral

, 0 ≤ δ

(∆V ) ≤ 2r (17)

The number of sweepers, the half-angle of their sensors and

the sweep cycle number (the number representing the number

of sweeps already completed by the sweeping team around the

evader region) all inﬂuence the distance sweepers are able to

progress inwards toward the center of the evader region after

completing a sweep. If the evader region was not expanding

throughout the sweepers’ inward motion, then δ

(∆V ) is,

(∆V ) = 2r − (R

− r) (λ − 1) (18)

In the expression δ

(∆V ), ∆V expresses the sweeper’s excess

speed above the critical speed. Denote by i the sweep cycle

number that starts from sweep number 0. As mentioned earlier

in the development of the critical speed, the time required for

sweepers to advance toward the center of the evader region

up to the point in which their sensors fully overlap the evader

region depends on the relative speed between the sweepers

inwards entry speed and the evader region outwards expansion

speed. Hence, after sweepers ﬁnish a sweep they advance

toward the center of evader region by a distance of,

ef f

(∆V ) = δ

(∆V )



+ V



(19)

Following the completion of a sweep around the region,

sweeper pairs progress together in the direction of the evader

region’s center. During inwards motions, sweepers move at

speed of V

, up to the point in which they begin to spirally

sweep again once their sensors are fully over the evader

region’s expanding wavefront. Therefore, their speed is always

bounded. We assume as a worst-case assumption, that the

sweeper’s sensors detect evaders only when sweepers perform

spiral motions. Therefore, throughout inward motions no de-

tection of evaders occurs, while the evader region continues to

expand due to motions of evaders. In the video accompanying

the paper, the time it takes the sweepers to advance inwards

is taken into account and dictates the new radius of the evader

region after the sweep. Hence, after an inward advancement

the evader region is within a circle whose radius is,

i+1

= R

− δ

(∆V )



+ V



(20)

Denote by

= R

−r. The usage of

allows to analytically

solve for the number of sweeps required to complete the search

of the entire evader region. Replacing δ

(∆V ) into (20) yields

the following difference equation,

i+1



+ V



−

2rV

+ V

(21)

Denote the coefﬁcients of (21) by, c

= −

2rV

, c

. Hence,

i+1

= c

+ c

(22)

Denote by R

the radius of the circle bounding the evader

region when it is shrunk to be within a circle having a radius

smaller or equal to 2r. Calculating R

is possible only after

the number of sweeps around the region, N

, is calculated.

Hence, we use

= 2r as an estimate of R

to allow the

calculation of N

. The number of sweeps required to decrease

the evader region to be within a circle of radius

= 2r is,







r(3−λ)

(1−λ)+r(1+λ)











(23)

The ceiling operator is used since the number of sweeps

must be integer. This means that sweepers continue sweep

number N

even if the evader region’s radius is reduced to

less 2r throughout the ﬁnal spiral sweep. Hence, to facilitate

the calculation of N

we assume the last sweep occurs when

the evader region is within a circle of radius

= 2r. Denote

by T

the duration of each inwards motion. It is a function

of the sweep cycle number and equals,

ef f

(∆V )

2r −

(λ − 1)

+ V

(24)

Denote the sum of all inward advancement times up to the

point in which the evader region is within a circle of radius

smaller than or equal to 2r as

(n), i.e.

(n) =

−2

i=0

During inwards motions the sweepers’ sensors are not fully

inside the evader region, hence they detect evaders in locations

that are already free from evaders. Hence, we assume that

sweepers do not detect evaders until they complete their

inward motion and begin sweeping again. The total sweep

times until the evader region is within a circle having a radius

less than or equal to 2r is computed as the addition of the total

spiral sweep times and the total inward advancement times.

Therefore,

T (n) =

(n) +

spiral

(n) (25)

The sum of all inward motion times until the evader region

is reduced to be within a circle having a radius less than or

equal to 2r is,

(n) =

−2

i=0

−r

2r(V

λ)

)(1−λ)

−

λ)

−1

)(1−λ)

(1 − λ) + r (1 + λ))

(26)

During the ﬁnal inward motion, sweepers advance toward

the region’s center and place the inner tips of the central part

of their sensors at the center of the evader region. Afterwards,

the sweepers perform a ﬁnal circular sweep and complete the

detection of all evaders in the region. The time required to

perform this motion is denoted by T

last

(n) and is given by

last

(n) =

, resulting in,

= −

1 − λ

+ c



(1 − λ) + r (1 + λ)

1 − λ



(27)

By replacing the exact value of R

from (27) in T

last

(n)

we obtain,

last

(n) = −

(1 − λ)

+ c



(1 − λ) + r (1 + λ)

(1 − λ)



(28)

The time required for sweeping around radius

is computed

by multiplying

λ−1

. Hence, multiplying (21) by

λ−1

yields the following sweep times difference equation,

i+1

= c

+ c

(29)

Where c

−2rV

(λ−1)

. The equation for computing the total

spiral sweep times up to the point at which the evader region

is within a circle of radius less or equal to 2r is,

spiral

(n) =

− c

−1

+ (N

− 1) c

1 − c

(30)

Replacing the coefﬁcients into (30) provides,

spiral

(n) =

(r−R

)(V

)

−

2r(V

λ)

(1−λ)

2r(N

−1)

−







)(R

(λ−1)−r(λ+1))

(1−λ)



(31)

C. The End-game

Following the sweepers’ completion of sweep number

− 1, they progress in the direction of the center of the

evader region up to a position in which the inner tips of the

central parts of their sensors are positioned at the center of the

evader region. After this inward motion, the sweepers must

complete a set of maneuvers referred to as the end-game in

order to ensure detection of all smart evaders. A ﬁnal circular

sweep around radius r is required to complete the detection of

all evaders and complete the search mission. Sweepers have

the ability to successfully detect all evaders during the last

circular sweep only if their speed is sufﬁciently high to ensure

that although they do not track the expanding wavefront of

the remaining evader region at this last sweep with a spiral

trajectory and perform a considerably less efﬁcient circular

sweep, they are still able to catch all evaders. The reason why

this last motion cannot be a spiral out motion is because we

wish that the tips of the central part of the sweepers sensors

will always be positioned at the center of the evader region to

ensure that no evaders remain at the center of the region or

near its vicinity. Due to the fact that the critical speed for a

spiral sweep is lower compared to a critical speed of circular

trajectories, the sweepers can only implement the last circular

sweep after spiral sweep number N

− 1 if their speeds are

sufﬁciently high and satisfy the following inequality,

2r ≥ V

last

+ V

last

+ R

(32)

Satisfying (32) implies that detection of all evaders is guar-

anteed. Prior to the last sweep the evader region is within a

circle of radius R

such that 0 < R

≤ 2r. R

can be also

expressed as, R

= r (2 − ε). Hence, ε may be expressed as

ε =

2r−R

, 0 ≤ ε < 2. The ﬁnal circular sweep takes place

once the sweepers progress to the region’s center and place

the lower tips of the central part of their sensors at the center

of the evader region. Hence, the last circular sweep is spans

an angle of

2π

− γ

around a region contained within a circle

of radius r around the center of the evader region. The time

required for sweepers to perform this motion is,

last

(n) =



2π

− 2α



(33)

Denote the smallest possible ε that satisﬁes (32) as ε

. To

perform the last circular sweep immediately following spiral

sweep number N

− 1, the inequality in (32) implies that

ε ≥ ε

(π−n(α−1))

n(V

)

. This consideration dictates that

implementation of a circular sweep immediately after spiral

sweep number N

− 1, V

is possible only if,

≥

(π − n (α − 1)) − nε

nε

(34)

If R

≥ r (2 − ε

) or equivalently,

≥

2rn (V

+ V

) − 2V

r (π − n (α − 1))

n (V

+ V

)

(35)

Then the sweepers’ speed does not sufﬁce to rule out the

possibility of a feasible escape trajectory for potential evaders.

Hence, if (35) holds or (34) does not, then the sweepers must

implement a ﬁnal spiral sweep, that starts with the lower

tips of the central parts of their sensors at the center of the

evader region. This spiral sweep starts when the center of

each sweeper is at a distance of r from the center of the

region. Denote by T

(n) the time required to sweep it. Hence,

(n) equals T

(n) =

r(λ−1)

. Denote by η a characteristic

function that assumes only two possible values, 1 or 0. If the

additional spiral sweep has to be implemented than η = 1 and

consequently T

(n) is added to the total sweep time, otherwise

in case no additional spiral sweep is required η = 0. Hence,

(n) =

r (λ − 1)

(36)

spiral

(n) =

spiral

(n) + T

last

(n) + ηT

(n) (37)

Denote by T

(n) the sweepers inward advancement time

corresponding to the spread of evaders originating from the

center of the evader region at the beginning of the last spiral

sweep that had time of T

(n) to spread at a speed of V

Therefore, T

(n) is given by T

(n) =

(n)V

. T

(n),

the total inward advancement time therefore equals,

(n) =

(n) + T

last

(n) + ηT

(n) (38)

Or alternatively,

(n) =

(n) +

ηr (λ − 1)

(39)

D. Experimental Results

Fig. 3 presents a numerical analysis of the total sweep times

required to detect all evaders in the region for different even

numbers of sweepers (2 to 16 sweepers). The total sweep times

are the sum of spiral sweep and inward advancement times.

5 10 15

500

1,000

1,500

2,000

Number of Agents

Time

Time of Complete Cleaning of

the Evader Region- α= 10

◦

∆V = 0.5V

∆V = 2V

∆V = 5V

∆V = 10V

2 4 6 8

Number of Agents * 2

T (2)

T (n)

Gain in Adding More

Sweepers- α= 10

◦

5 10 15

100

Number of Agents

Time

Total Inward Advancement

Times- α= 10

◦

5 10 15

500

1,000

1,500

2,000

Number of Agents

Time

Total Spiral Sweep

Times- α= 10

◦

Fig. 3. Sweep time until complete cleaning. The top left plot shows complete

cleaning times for different numbers of sweepers. The top right plot shows the

gain in search time reduction as a function of the number of sweepers. The

bottom left plot shows only the spiral sweep time component and the bottom

right plot shows only the inward advancement time component. The chosen

values of the parameters are: α = 10

◦

, r = 100, V

= 1 and R

= 1000.

V. CONCLUSIONS AND FUTURE RESEARCH DIRECTIONS

This research studies the problem of guaranteed detection of

smart mobile evaders by a team of sweeping agents equipped

with fan-shaped sensors that act as visual detectors. Evaders

are initially located inside a known circular environment that

does not have physical barriers that prevent evaders from

attempting to escape it. An algorithm that guarantees detection

of all evaders by using any even number of sweepers that

use pincer sweeps between searching pairs is developed and

analytically proven. Numerical and illustrative simulations

using MATLAB and NetLogo demonstrate the performance

of the proposed algorithm.

While in this work we focus on the rather simplistic circular

environment, the concept of spiral pincer movements based

on pairs of sweepers can be extended and generalized to

more complex environments with different geometric layouts.

Hence, a future research direction is to generalize the results

to environments with different geometries.

An additional future extension seeks to analyze critical

speeds and sweep times obtained for teams of sweepers with

fan-shaped sensors that employ same-direction sweeps. We ex-

pect such methods to result in degraded performance compared

to the pincer-based protocols developed in this work. Such

protocols will enable to precisely quantify the performance

improvement achieved with the developed pincer-based search

protocols compared to their same-direction alternatives.

REFERENCES

[1] M. Sandler, A. Howard, M. Zhu, A. Zhmoginov, and L.-C. Chen,

“Mobilenetv2: Inverted residuals and linear bottlenecks,” in Proceedings

of the IEEE conference on computer vision and pattern recognition,

2018, pp. 4510–4520.

[2] A. Bochkovskiy, C.-Y. Wang, and H.-Y. M. Liao, “Yolov4: Op-

timal speed and accuracy of object detection,” arXiv preprint

arXiv:2004.10934, 2020.

[3] B. O. Koopman, Search and screening: general principles with historical

applications. Oxford: Pergamon Press, 1980.

[4] P. Vincent and I. Rubin, “A framework and analysis for cooperative

search using uav swarms,” in Proceedings of the 2004 ACM symposium

on Applied computing. ACM, 2004, pp. 79–86.

[5] Y. Altshuler, V. Yanovsky, I. A. Wagner, and A. M. Bruckstein, “Efﬁcient

cooperative search of smart targets using uav swarms,” Robotica, vol. 26,

no. 4, pp. 551–557, 2008.

[6] Y. Altshuler, V. Yanovski, I. A. Wagner, and A. M. Bruckstein, “Multi-

agent cooperative cleaning of expanding domains,” The International

Journal of Robotics Research, vol. 30, no. 8, pp. 1037–1071, 2011.

[7] A. Bressan, M. Burago, A. Friend, and J. Jou, “Blocking strategies for

a ﬁre control problem,” Analysis and Applications, vol. 6, no. 03, pp.

229–246, 2008.

[8] A. Bressan and T. Wang, “On the optimal strategy for an isotropic block-

ing problem,” Calculus of Variations and partial differential equations,

vol. 45, no. 1-2, pp. 125–145, 2012.

[9] Z. Tang and U. Ozguner, “On non-escape search for a moving target by

multiple mobile sensor agents,” in 2006 American Control Conference.

IEEE, 2006, pp. 6–pp.

[10] T. G. McGee and J. K. Hedrick, “Guaranteed strategies to search for

mobile evaders in the plane,” in 2006 American Control Conference.

IEEE, 2006, pp. 6–pp.

[11] P. C. Hew, “Linear and concentric arc patrols against smart evaders,”

Military Operations Research, vol. 20, no. 3, pp. 39–48, 2015.

[12] D. Shishika and V. Kumar, “Local-game decomposition for multiplayer

perimeter-defense problem,” in 2018 IEEE Conference on Decision and

Control (CDC). IEEE, 2018, pp. 2093–2100.

[13] D. Shishika, J. Paulos, and V. Kumar, “Cooperative team strategies for

multi-player perimeter-defense games,” IEEE Robotics and Automation

Letters, vol. 5, no. 2, pp. 2738–2745, 2020.

[14] V. R. Makkapati and P. Tsiotras, “Optimal evading strategies and task

allocation in multi-player pursuit–evasion problems,” Dynamic Games

and Applications, vol. 9, no. 4, pp. 1168–1187, 2019.

[15] T. H. Chung, G. A. Hollinger, and V. Isler, “Search and pursuit-evasion

in mobile robotics,” Autonomous robots, vol. 31, no. 4, pp. 299–316,

2011.

[16] S. S. Kumkov, S. Le M

enec, and V. S. Patsko, “Zero-sum pursuit-evasion

differential games with many objects: survey of publications,” Dynamic

games and applications, vol. 7, no. 4, pp. 609–633, 2017.

[17] I. E. Weintraub, M. Pachter, and E. Garcia, “An introduction to pursuit-

evasion differential games,” in 2020 American Control Conference

(ACC). IEEE, 2020, pp. 1049–1066.

[18] E. Garcia, D. W. Casbeer, and M. Pachter, “Optimal strategies of the

differential game in a circular region,” IEEE Control Systems Letters,

vol. 4, no. 2, pp. 492–497, 2019.

[19] E. Garcia, D. W. Casbeer, A. Von Moll, and M. Pachter, “Multiple

pursuer multiple evader differential games,” IEEE Transactions on

Automatic Control, vol. 66, no. 5, pp. 2345–2350, 2020.

[20] R. M. Francos and A. M. Bruckstein, “Search for smart evaders with

swarms of sweeping agents,” IEEE Transactions on Robotics, vol. 38,

no. 2, pp. 1080–1100, 2021.

[21] R. Francos and A. Bruckstein, “Pincer-based vs. same-direction search

strategies after smart evaders by swarms of agents,” Proceedings of the

IEEE International Conference on Ubiquitous Robots; arXiv preprint

arXiv:2104.06940, 2023.

[22] S. Tisue and U. Wilensky, “Netlogo: A simple environment for modeling

complexity,” in International conference on complex systems, vol. 21.

Boston, MA, 2004, pp. 16–21.

[23] R. M. Francos and A. M. Bruckstein, “Search for smart evaders with

sweeping agents,” Robotica, pp. 1–36, 2021.