Chapter 4
Group theory
Group theory will be presented in this chapter as a tool for spectroscopy. Indeed group theory
makes it possible to
• construct and classify molecular orbitals,
• classify electronic, vibrational, rotational and nuclear spin wave functions,
• predict which states are allowed,
• predict physical properties (existence of electric dipole moment, optical activity etc.),
• predict selection rules (electric dipole transitions, configuration interaction. etc.)
However, group theory does not make any quantitative predictions. The interest of group
theory lies in simplifying some problems like those mentioned above that arise in molecular
spectroscopy.
4.1 Symmetry operations
4.1.1 Definition of a group
A group G is a set of elements A, B, C, ... connected by a combination rule (written as a
product, for example A · B) which has the following properties:
1. the closure: for all elements A and B of the group G, A · B = C is also an element of
the group G.
2. the associativity: the combination rule must be associative, i. e. A·(B·C)=(A·B)·C.
3. the identity: there must be an element, the identity E (also called unit), such that
E · R = R · E = R for all elements R of the group.
4. the inverses:eachelementR must have an inverse R
−1
which is also a group element
such that R · R
−1
= R
−1
· R = E.
101

102 CHAPTER 4. GROUP THEORY
In group theory, the elements considered are symmetry operations. For a given molecular
system described by the Hamiltonian
ˆ
H, there is a set of symmetry operations
ˆ
O
i
which
commute with
ˆ
H:
ˆ
O
i
,
ˆ
H
=0. (4.1)
ˆ
H and
ˆ
O
i
thus have a common set of eigenfunctions and the eigenvalues of
ˆ
O
i
can be used
as labels for the eigenfunctions (see Lecture Physical Chemistry III). This set of operations
defines (with the multiplication operation) a symmetry group. In molecular physics and
molecular spectroscopy two types of groups are particularly important, the point groups and
the permutation-inversion groups.
4.1.2 Point group operations and point group symmetry
The point groups adequately describe molecules that can be considered as rigid on the
timescale of the spectroscopic experiment, which means molecules that have a unique equi-
librium configuration with no observable tunneling between two or more equivalent configu-
rations.
The symmetry operations of the point groups are:
• the identity E which leaves all coordinates unchanged.
• the proper rotation C
n
by an angle of 2π/n in the positive trigonometric sense (i. e.
counter-clockwise). The symmetry axis with highest n is chosen as principal axis. If
a molecule has a unique C
n
axis with highest n, the molecule has a permanent dipole
moment that lies along this axis (e. g. H
2
O, NCl
3
in Figure 4.1). If a molecule has
several C
n
axes with highest n, the molecule has no permanent dipole moment (e. g.
CH
4
).
O
H
H
C
2
N
Cl
Cl
C
3
Cl
Figure 4.1: C
2
rotation of H
2
OandC
3
rotation of NCl
3
.
• the reflection through a plane σ; the reflections are classified into two categories:
PCV - Spectroscopy of atoms and molecules
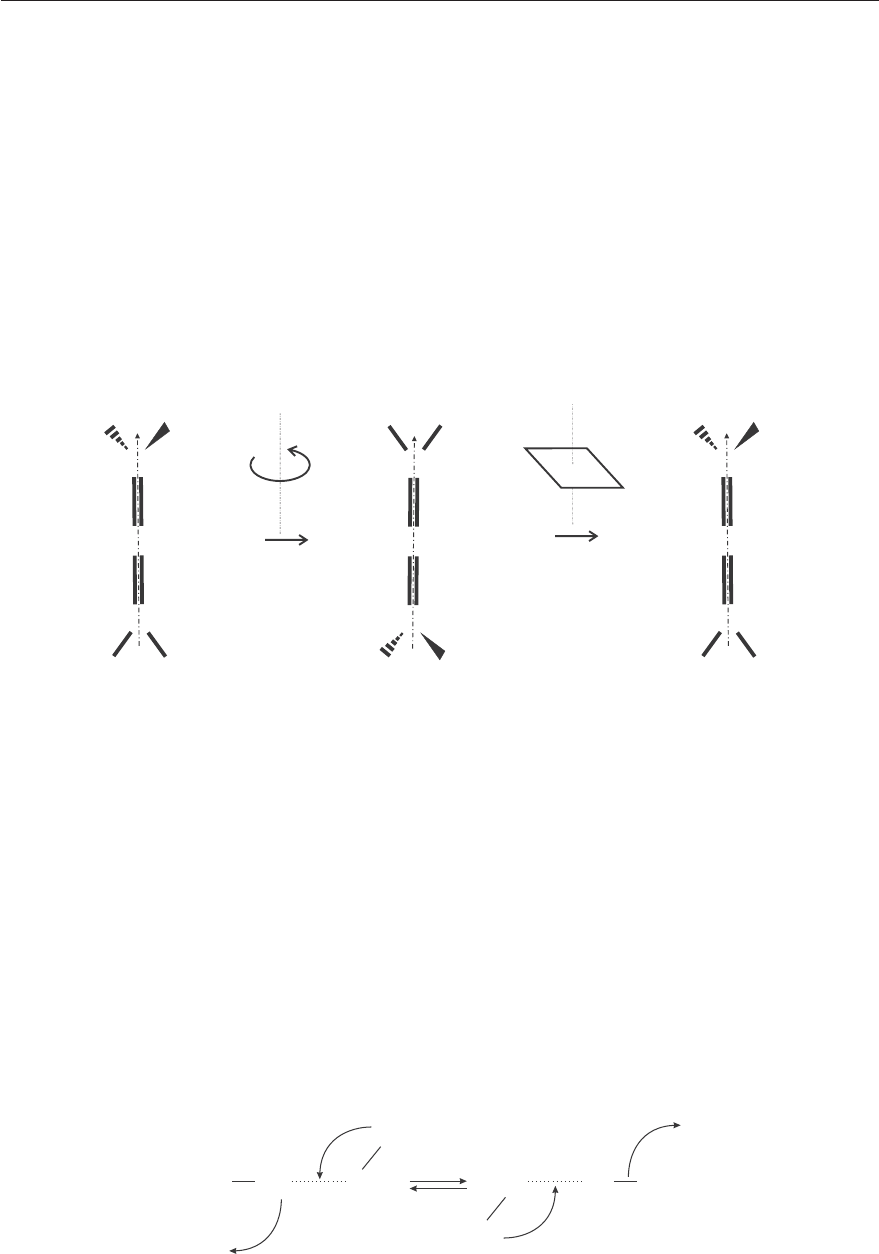
4.1. SYMMETRY OPERATIONS 103
– the reflections through a vertical plane, i. e. a plane which contains the symmetry
axis z are noted σ
v
,
– the reflections through an horizontal plane, i. e. a plane perpendicular to the
symmetry axis z are noted σ
h
.
• the inversion i of all coordinates through the inversion center.
• the improper rotation S
n
or rotation-reflection which consists in a rotation by an
angle of 2π/n around the z axis followed by a reflection through the plane perpendicular
to the rotational axis. Figure 4.2 shows the S
4
improper rotation of allene as an example.
z
(1)
C
(2)
C
(3)
C
(1)
H
(2)
H
(3)
H
(4)
H
xy
s
C
4
z
(3)
C
(2)
C
(1)
C
(1)
H
(2)
H
(3)
H
(4)
H
z
(1)
C
(2)
C
(3)
C
(3)
H
(4)
H
(1)
H
(2)
H
Figure 4.2: Decomposition of the improper rotation S
4
of allene.
A molecule having an improper operation as symmetry operation, i. e. a reflection, an im-
proper rotation or an inversion, cannot be optically active and is therefore achiral.
4.1.3 Permutation-inversion operations and CNPI groups
As mentioned already, the point groups are well suited to describe rigid molecules. However,
for floppy systems, especially clusters with tunneling splitting as shown in Figure 4.3, or when
the transition between two states does not hold the same symmetry, another, more general
definition is required.
F
(2)
H
(2)
F
(1)
H
(1)
F
(2)
H
(2)
H
(1)
F
(1)
Figure 4.3: Tunneling process in (HF)
2
.
To circumvent this problem, the complete nuclear permutation inversion (CNPI) groups have
PCV - Spectroscopy of atoms and molecules

104 CHAPTER 4. GROUP THEORY
been developed, originally by Christopher Longuet-Higgins and Jon T. Hougen (see Bunker
and Jensen, Molecular Symmetry and Spectroscopy, 1998). Their concept relies on the fact
that the symmetry operations, i. e. the permutation-inversion operations leave
ˆ
H unchanged.
The symmetry operations of the CNPI groups are:
• the permuation (ij) of the coordinates of two identical nuclei i and j which denotes
the exchange of the nucleus i with the nucleus j (see Figure 4.4 for examples),
• the cyclic permutation (ijk) of the coordinates of three identical nuclei i, j,andk,
i. e. the nucleus i will be replaced by the nucleus j, j by k and k by i (see Figure 4.4
for example),
O
H
(2)
H
(1)
(12)
O
H
(1)
H
(2)
N
H
(2)
H
(1)
(123)
H
(3)
N
H
(3)
H
(2)
H
(1)
H
(2)
F
(2)
F
(1)
H
(1)
(12)
H
(1)
F
(1)
F
(2)
H
(2)
Figure 4.4: Examples of (ij)and(ijk) permutations.
• all possible circular permutations of n identical nuclei (for example, the (1 2 3 4 5 6)
permutation in benzene),
• the inversion E
∗
of all coordinates of all particles through the center of the lab-fixed
frame,
• the permutationfollowedbyaninversion(ij)
∗
= E
∗
· (ij)ofallcoordinatesofall
particles
• the cyclic permutation followed by an inversion (ijk)
∗
of all coordinates of all
particles,
• all possible circular permutations followed by an inversion of all coordinates of n iden-
tical nuclei.
PCV - Spectroscopy of atoms and molecules

4.2. IMPORTANT CONCEPTS IN A GROUP 105
The permutation operations only affect identical nuclei, therefore the molecular Hamiltonian
is left unchanged upon these operations. Moreover the molecular Hamiltonian depends on
distances rather than positions, hence the inversion operation also leaves
ˆ
H unchanged.
The CNPI groups represent a more general description that can also be applied to rigid
molecules. Indeed each point group is isomorphous to a CNPI group although the symmetry
operations are not identical (for example, the inversion i of a point group symmetry is not
the same as the inversion of a permutation inversion group E
∗
).
———————————————————
Example: the point group C
3v
is isomorphous to S
3
= {E,(1 2 3), (1 3 2), (1 2), (1 3), (2 3)},which
means that there is a one to one correspondence between the two sets of operations.
———————————————————
However, one disadvantage of the CNPI groups is their size which can become very large. For
example, the CNPI for CH
4
contains 48 symmetry operations, and that of benzene 1036800!
In the case of non-rigid systems, this problem is usually solved by using a subgroup, i. e. a
subset of the group which forms a group under the same combination rule. These subgroups
are called molecular symmetry (MS) groups.
In the case of rigid molecules, most of the time the point groups are used. In the following,
we will consider rigid molecules only and restrict ourselves to point group symmetry, but all
concepts can be extended to the CNPI and MS groups.
4.2 Important concepts in a group
4.2.1 Order, conjugated elements and classes
The order of a group is equal to the number of elements in the group. The discrete
(or finite) groups have a finite order (for example C
2v
is a group of fourth order), while
continuous groups have infinite orders (C
∞v
for example).
Let us consider two operations
ˆ
O
i
and
ˆ
O
j
that leave
ˆ
H unchanged when applied individually.
Hence, they must also leave
ˆ
H unchanged when applied in succession. The notation
ˆ
O
i
·
ˆ
O
j
means that
ˆ
O
j
acts first, and
ˆ
O
i
second. In other words,
ˆ
O
i
·
ˆ
O
j
must be a symmetry operation
ˆ
O
k
if
ˆ
O
i
and
ˆ
O
j
are symmetry operations, which is a corollary of the closure property of a
group. Very often it is useful to build the so-called multiplication table which summarizes
all possible
ˆ
O
i
·
ˆ
O
j
combinations.
———————————————————
PCV - Spectroscopy of atoms and molecules
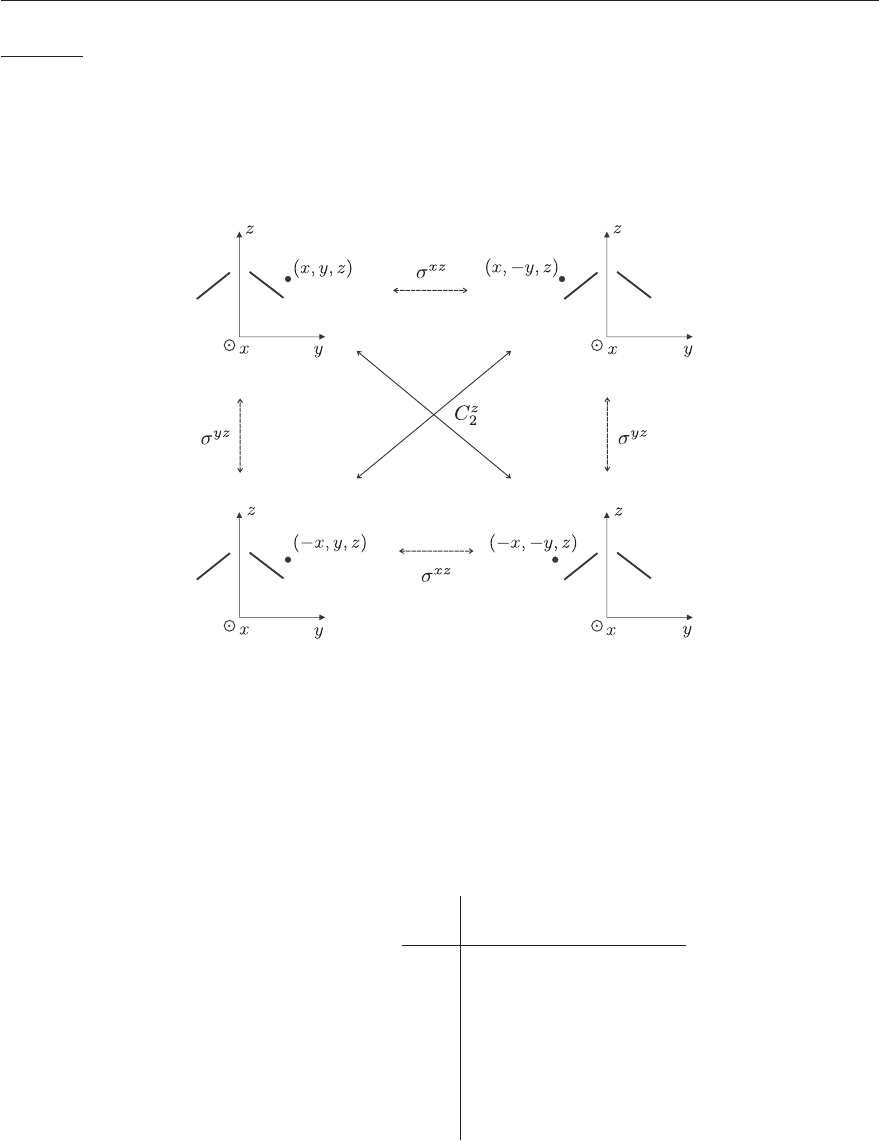
106 CHAPTER 4. GROUP THEORY
Example: the C
2v
group of H
2
O
The symmetry operations are E, C
z
2
, σ
xz
and σ
yz
. From Figure 4.5 one can verify that the successive
application of any two operations of the C
2v
point group is equivalent to the application of a third
group operation. For instance: σ
xz
· σ
yz
= C
z
2
, σ
xz
· σ
xz
= E, C
z
2
· σ
xz
= σ
yz
,etc.
Figure 4.5: C
2v
group operations and their effect on a water molecule. The dot indicates
schematically the coordinates (x, y, z) of an electron.
The multiplication table of the C
2v
point group with four symmetry operations (E, C
z
2
, σ
xz
, σ
yz
)is
thus a 4×4 table.
1
st
operation (right)
C
2v
EC
z
2
σ
xz
σ
yz
2
nd
operation (left)
E
EC
z
2
σ
xz
σ
yz
C
z
2
C
z
2
Eσ
yz
σ
xz
σ
xz
σ
xz
σ
yz
EC
z
2
σ
yz
σ
yz
σ
xz
C
z
2
E
Table 4.1: Multiplication table of the C
2v
point group.
———————————————————
AgroupG is said abelian or commutative when all operations commute:
ˆ
O
i
·
ˆ
O
j
=
ˆ
O
j
·
ˆ
O
i
. (4.2)
PCV - Spectroscopy of atoms and molecules
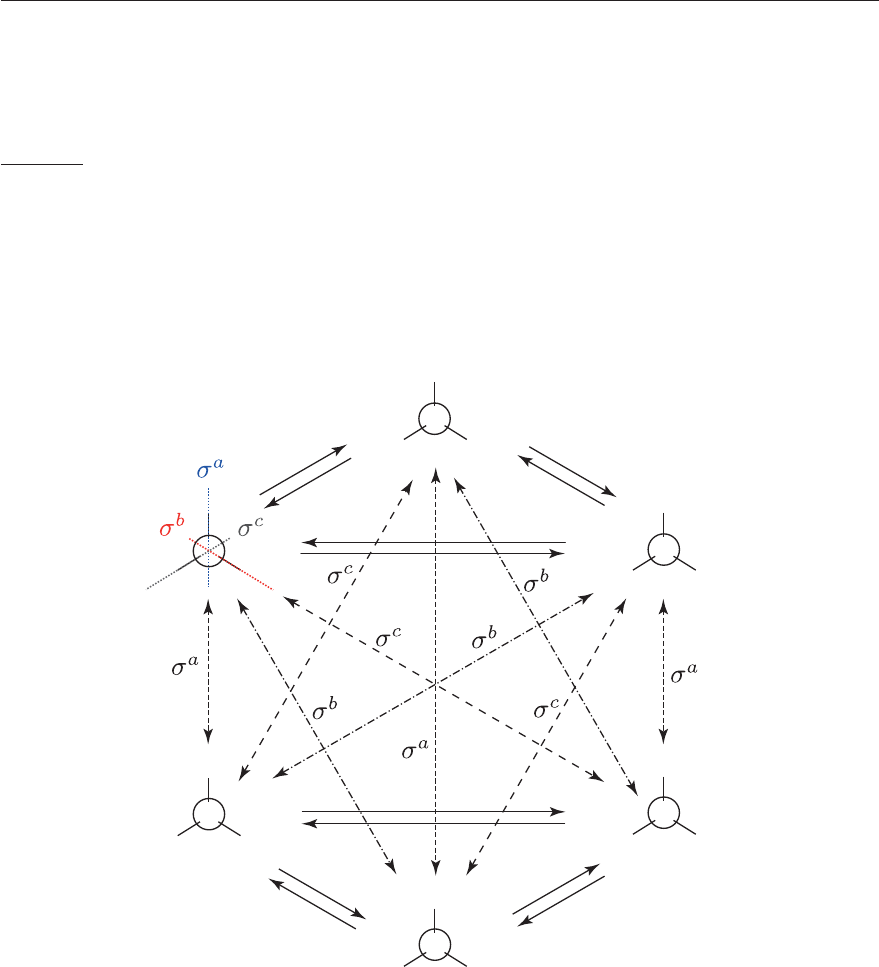
4.2. IMPORTANT CONCEPTS IN A GROUP 107
For example, the C
2v
group is abelian (see Table 4.1). However, not all groups are Abelian.
An example of a non-abelian group is the point group C
3v
.
———————————————————
Example: CH
3
Cl in the C
3v
group
The symmetry operations are E, C
3
, C
2
3
, σ
a
, σ
b
, σ
c
, hence the group is of order 6. With the help of
Figure 4.6, one can derive the multiplication table of the C
3v
point group. One sees that the group is
not Abelian because not all operations commute (e. g., C
3
· σ
a
= σ
c
and σ
a
· C
3
= σ
b
). Moreover, not
all operations are their own inverse (e. g., C
3
· C
3
= E).
Figure 4.6: The operations of the C
3v
point group with the example of the CH
3
Cl molecule
represented as a Newmann projection (adapted from F. Merkt and M. Quack in Handbook of
high-resolution spectroscopy, 2011).
PCV - Spectroscopy of atoms and molecules

108 CHAPTER 4. GROUP THEORY
1
st
operation (right)
C
3v
EC
3
C
2
3
σ
a
σ
b
σ
c
2
nd
operation (left)
E
EC
3
C
2
3
σ
a
σ
b
σ
c
C
3
C
3
C
2
3
Eσ
c
σ
a
σ
b
C
2
3
C
2
3
EC
3
σ
b
σ
c
σ
a
σ
a
σ
a
σ
b
σ
c
EC
3
C
2
3
σ
b
σ
b
σ
c
σ
a
C
2
3
EC
3
σ
c
σ
c
σ
a
σ
b
C
3
C
2
3
E
Table 4.2: Multiplication table of the C
3v
point group.
———————————————————
If
ˆ
O
i
,
ˆ
O
j
,and
ˆ
O
k
are all group elements and if they obey the relation
ˆ
O
k
·
ˆ
O
i
·
ˆ
O
−1
k
=
ˆ
O
j
, (4.3)
then
ˆ
O
i
and
ˆ
O
j
are called conjugated elements. All conjugated elements in a group form
aclass.
———————————————————
Example: Elements of the point group C
3v
that belong to the same class as C
3
We consider C
3
=
ˆ
O
i
and apply each operation
ˆ
O
k
of C
3v
according to Equation (4.3) with the help
of the multiplication table in order to find the conjugated elements of C
3
.
ˆ
O
i
ˆ
O
k
ˆ
O
−1
k
ˆ
O
k
·
ˆ
O
i
·
ˆ
O
−1
k
=
ˆ
O
j
ˆ
O
i
ˆ
O
k
ˆ
O
−1
k
ˆ
O
k
·
ˆ
O
i
·
ˆ
O
−1
k
=
ˆ
O
j
C
3
E E E · C
3
· E = C
3
C
2
3
E E E · C
2
3
· E = C
2
3
C
3
C
3
C
2
3
C
3
· C
3
· C
2
3
= C
3
C
2
3
C
3
C
2
3
C
3
· C
2
3
· C
2
3
= C
2
3
C
3
C
2
3
C
3
C
2
3
· C
3
· C
3
= C
3
C
2
3
C
2
3
C
3
C
2
3
· C
2
3
· C
3
= C
2
3
C
3
σ
a
σ
a
σ
a
· C
3
· σ
a
σ
c
= C
2
3
C
2
3
σ
a
σ
a
σ
a
· C
2
3
· σ
a
σ
b
= C
3
C
3
σ
b
σ
b
σ
b
· C
3
· σ
b
σ
a
= C
2
3
C
2
3
σ
b
σ
b
σ
b
· C
2
3
· σ
b
σ
c
= C
2
3
C
3
σ
c
σ
c
σ
c
· C
3
· σ
c
σ
b
= C
2
3
C
2
3
σ
c
σ
c
σ
c
· C
2
3
· σ
c
σ
a
= C
2
3
C
3
and C
2
3
are conjugated; they are elements of the same class of order 2.
Similarly, one can show that σ
a
, σ
b
and σ
c
form a class of order 3.
———————————————————
The order k of an element
ˆ
O
i
is the smallest integer k ≥ 1with
ˆ
O
k
i
= E. This property
PCV - Spectroscopy of atoms and molecules

4.2. IMPORTANT CONCEPTS IN A GROUP 109
exists for finite groups only.
With this definition, one can easily find that a rotation C
n
is of order n and a reflection σ is
of order 2. All elements of a class have the same order.
4.2.2 Representations and character table
Up to now, we have described each symmetry operation
ˆ
O of a group with respect to one
specific molecule. Now, we would like to get a more general picture and represent each
operation of the group with a n×n matrix B, n being the dimensionality of the representation.
This matrix represents how the vectors or functions chosen as basis set (of dimension n)
transform upon the application of
ˆ
O. Therefore, the matrix B depends on the coordinate
system, i. e. the vectors chosen to describe the system. Given a coordinate system ˜e,the
matrix representation B
(˜e)
of the operation
ˆ
O fulfils
y = B
(˜e)
x. (4.4)
With a new coordinate system ˜e
= S ˜e, the transformation is
y
= Sy,and
x
= Sx.
Therefore
y
= Sy = SB
(˜e)
x = SB
(˜e)
S
−1
x
= B
(˜e
)
x
(4.5)
The matrix B
(˜e
)
= SB
(˜e)
S
−1
forms a new, equivalent representation of the operation
ˆ
O.
The trace of a matrix remains unchanged upon an unitary coordinate transformation. Thus
Tr(B
(˜e
)
)=Tr(B
(˜e)
). (4.6)
The trace of a matrix representing an operation is also called the character of the opera-
tion χ. An interesting property is that all elements of a class have the same character.
———————————————————
Example : one-dimensional representation (n =1)ofC
2v
Case 1: one can use the functions Ψ
1
= x, Ψ
2
= y,orΨ
3
= z.
Ψ
1
= x : Ex= x Ψ
2
= y : Ey= y Ψ
3
= z : Ez= z
C
z
2
x = −xC
z
2
y = −yC
z
2
z = z
σ
xz
x = xσ
xz
y = −yσ
xz
z = z
σ
yz
x = −xσ
yz
y = yσ
yz
z = z
PCV - Spectroscopy of atoms and molecules
110 CHAPTER 4. GROUP THEORY
Therefore x, y,andz correspond to the following representations designated by Γ:
C
2v
EC
z
2
σ
xz
σ
yz
Γ
(z)
11 1 1
Γ
(x)
1 −11−1
Γ
(y)
1 −1 −11
Case 2:
instead of using x, y,orz, more complicated functions can be used to generate a one-
dimensional representation, such as x
2
, y
2
, z
2
, xy, xz or yz as listed in the fourth column of the
character table. For example, one takes the functions Ψ
4
= x
2
and Ψ
5
= xy:
Ψ
4
= x
2
: Ex
2
=(Ex)(Ex)=x
2
Ψ
5
= xy : Exy=(Ex)(Ey)=xy
C
z
2
x
2
=(C
z
2
x)(C
z
2
x)=x
2
C
z
2
xy =(C
z
2
x)(C
z
2
y)=xy
σ
xz
x
2
=(σ
xz
x)(σ
xz
x)=x
2
σ
xz
xy =(σ
xz
x)(σ
xz
y)=−xy
σ
yz
x
2
=(σ
yz
x)(σ
yz
x)=x
2
σ
yz
xy =(σ
yz
x)(σ
yz
y)=−xy
It is easy to verify that χ
(xy)
= χ
(x)
× χ
(y)
, a result that can be written as a direct product. To
evaluate a direct product, one multiplies the characters of each class of elements pairwise and
obtains as direct product a representation of the group:
Γ
(xy)
=Γ
(x)
⊗ Γ
(y)
=(1-11-1)⊗ (1 -1 -1 1) = (1 1 -1 -1).
Case 3:
one can also look at the transformation properties of rotations and for example take Ψ
6
= R
z
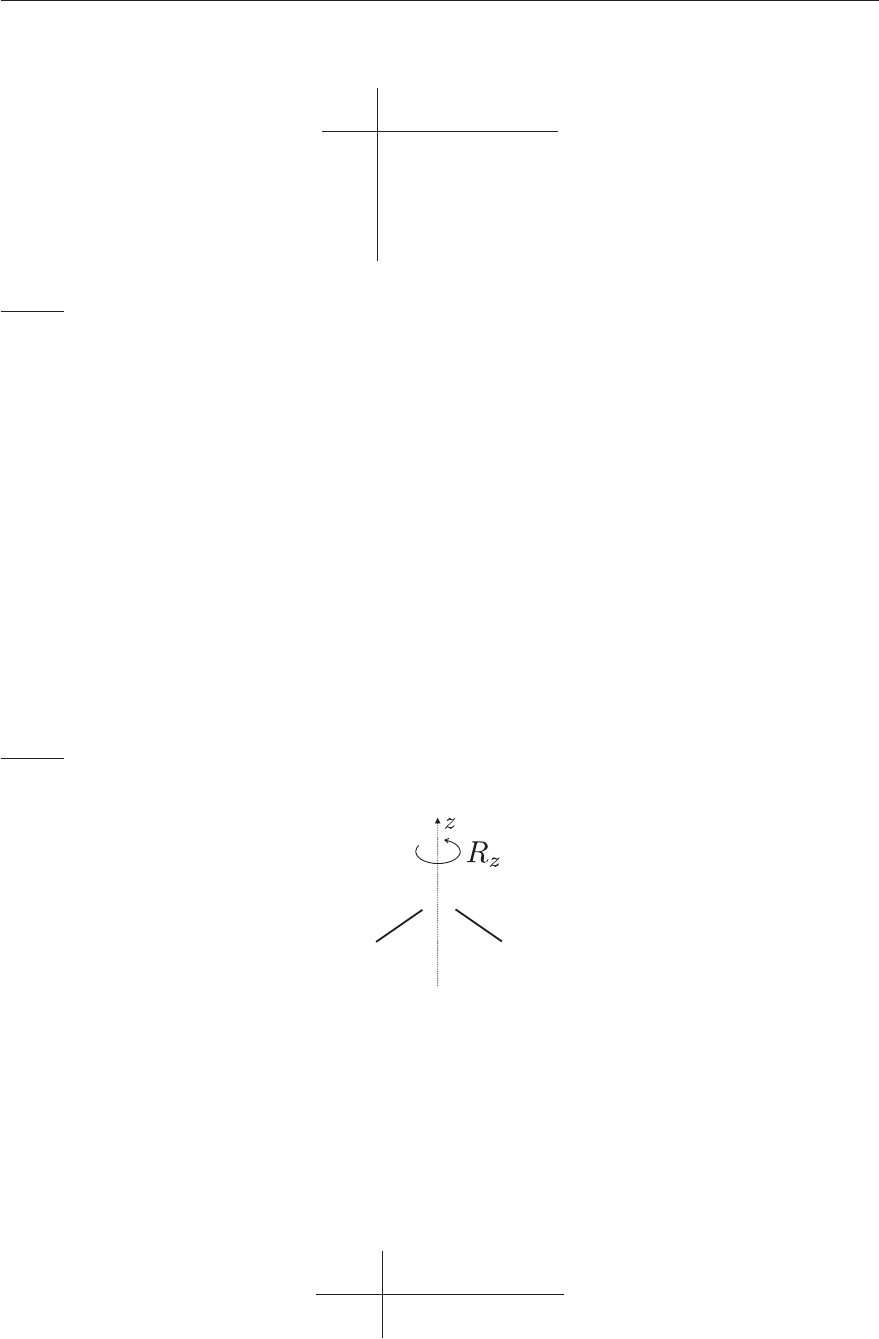
as illustrated in Figure 4.7.
Figure 4.7: The R
z
rotation of water.
Ψ
6
= R
z
: ER
z
= R
z
C
z
2
R
z
= R
z
σ
xz
R
z
= −R
z
Direction of rotation reversed.
σ
yz
R
z
= −R
z
Direction of rotation reversed.
R
z
transforms as follows:
C
2v
EC
z
2
σ
xz
σ
yz
Γ
(R
z
)
11−1 −1
———————————————————
PCV - Spectroscopy of atoms and molecules

4.2. IMPORTANT CONCEPTS IN A GROUP 111
Representations of higher dimensionality can be obtained by looking at the transformation
properties of two or more functions. Indeed, to construct an n-dimensional representation of
agroup,onetakesn linear independent functions or vectors Ψ
i
,i=1, ..., n spanning a given
n-dimensional space. Applying the group operations on Ψ
i
leads to a transformed function
which is a linear combination of the original functions:
ˆ
OΨ
i
=
n
j=1
b
ji
(
ˆ
O)Ψ
j
. (4.7)
———————————————————
Example: two dimensional representation
x
y
of the C
2v
group
E
⎛
⎜
⎝
x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
10
01
⎞
⎟
⎠
⎛
⎜
⎝
x
y
⎞
⎟
⎠
, with χ
(
x
y
)
E
=2
C
z
2
⎛
⎜
⎝
x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
−x
−y
⎞
⎟
⎠
=
⎛
⎜
⎝
−10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
x
y
⎞
⎟
⎠
, with χ
(
x
y
)
C
z
2
= −2
σ
xz
⎛
⎜
⎝
x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
x
−y
⎞
⎟
⎠
=
⎛
⎜
⎝
10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
x
y
⎞
⎟
⎠
, with χ
(
x
y
)
σ
xz
=0
σ
yz
⎛
⎜
⎝
x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
−x
y
⎞
⎟
⎠
=
⎛
⎜
⎝
−10
01
⎞
⎟
⎠
⎛
⎜
⎝
x
y
⎞
⎟
⎠
, with χ
(
x
y
)
σ
yz
=0
The two-dimensional representation of
x
y
has thus the following characters:
C
2v
EC
z
2
σ
xz
σ
yz
2 × 2 Matrix
⎛
⎜
⎝
10
01
⎞
⎟
⎠
⎛
⎜
⎝
−10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
−10
01
⎞
⎟
⎠
Γ
(
x
y
)
2 −200
———————————————————
If the matrices of all elements of a representation of a group can be simultaneously brought
into block-diagonal form by a given coordinate transformation, the representation is said to
be reducible,ifnot,itisirreducible.
The character table of a group lists all irreducible representations and gives for each rep-
resentation the character of each class of elements.
PCV - Spectroscopy of atoms and molecules
112 CHAPTER 4. GROUP THEORY
G C
1
= EC
2
... C
n
T
x
T
y
T
z
R
x
R
y
R
z
Γ
(1)
irr
χ
(1)
(C
1
) χ
(1)
(C
2
) ... χ
(1)
(C
n
)
Γ
(2)
irr
χ
(2)
(C
1
) χ
(2)
(C
2
)
.
.
.
.
.
.
.
.
.
Γ
(n)
irr
χ
(n)
(C
1
) χ
(n)
(C
2
) ... χ
(n)
(C
n
)
In a character table, Γ
(n)
designates the n-th irreducible representation, C
i
the i-th class of
elements and χ
(n)
(C
j
) the character of the elements of class j in the n-th representation.
There are as many irreducible representations as classes. Next to the characters of the el-
ements of the different classes, the character table also gives in the last columns how the
translations T
x
, T
y
and T
z
and the rotations R
x
, R
y
and R
z
transform.
———————————————————
Example: The character table of the C
2v
group
C
2v
EC
z
2
σ
xz
σ
yz
A
1
11 1 1z x
2
,y
2
,z
2
A
2
11−1 −1 xy R
z
B
1
1 −11−1 x xz R
y
B
2
1 −1 −11y yz R
x
x, y,andz correspond to the irreducible representations B
1
,B
2
,andA
1
, respectively as indicated in
the third column of the character table. R
z
transforms as A
2
as indicated in the fifth column of the
character table. One can verify that R
x
and R
y
transform as B
2
and B
1
, respectively.
The Γ
(
x
y
)
representation is not an irreducible representation of C
2v
because it is of dimension 2, and
C
2v
has one-dimensional irreducible representations only. Γ
(
x
y
)
is reducible, i. e., it corresponds to a
linear combination of irreducible representations: Γ
(
x
y
)
=B
1
⊕ B
2
.
———————————————————
Character tables exist for all groups. Many groups have a finite number of representations,
but groups with an infinite number of representations also exist such as D
∞h
and C
∞v
.
Important remark: The character of the unity operation (E) is always equal to the dimension
of the representation.
PCV - Spectroscopy of atoms and molecules

4.2. IMPORTANT CONCEPTS IN A GROUP 113
4.2.3 Reduction of reducible representations
There is a systematic mathematical procedure to perform the reduction of representations.
All representations in a character table form a set of orthogonal vectors that span the complete
space:
ˆ
O
χ
(i)
(
ˆ
O) × χ
(j)
(
ˆ
O)=hδ
ij
, (4.8)
where h represents the order of the group and
ˆ
O runs over all the elements of the group. (Note
that some classes of non-Abelian groups contain more than one element!). Any reducible
representation can thus be expressed as a linear combination of irreducible representations
Γ
red
=
k
c
red
k
Γ
(k)
, (4.9)
where Γ
(k)
represents an irreducible representation. The expansion coefficients c
red
k
can be
determined using the reduction formula Equation (4.10):
c
red
k
=
1
h
ˆ
O
χ
red
(
ˆ
O) × χ
k
(
ˆ
O) (4.10)
———————————————————
Example : two-dimensional representation spanned by 1s atomic orbitals
1s(1)
1s(2)
centred on the H
atoms of a water molecule H
2
OintheC
2v
group (see Figure 4.8)
O
H
(2)
H
(1)
Figure 4.8: 1s atomic orbitals on the H atoms of H
2
O.
E
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
10
01
⎞
⎟
⎠
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
thus χ
E
=2
C
z
2
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
1s(2)
1s(1)
⎞
⎟
⎠
=
⎛
⎜
⎝
01
10
⎞
⎟
⎠
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
thus χ
C
z
2
=0
σ
xz
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
1s(2)
1s(1)
⎞
⎟
⎠
=
⎛
⎜
⎝
01
10
⎞
⎟
⎠
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
thus χ
σ
xz
=0
σ
yz
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
=
⎛
⎜
⎝
10
01
⎞
⎟
⎠
⎛
⎜
⎝
1s(1)
1s(2)
⎞
⎟
⎠
thus χ
σ
yz
=2
PCV - Spectroscopy of atoms and molecules

114 CHAPTER 4. GROUP THEORY
C
2v
EC
z
2
σ
xz
σ
yz
A
1
11 11
A
2
11−1 −1
B
1
1 −11−1
B
2
1 −1 −11
2 × 2 Matrix
⎛
⎜
⎝
10
01
⎞
⎟
⎠
⎛
⎜
⎝
−10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
10
0 −1
⎞
⎟
⎠
⎛
⎜
⎝
−10
01
⎞
⎟
⎠
Γ
(1s)
20 02
Reduction of Γ
(1s)
=(2002):
c
(1s)
A
1
=
1
4
(2 × 1+0× 1+0× 1+2× 1) = 1
c
(1s)
A
2
=
1
4
(2 × 1+0× 1+0× (−1) + 2 × (−1)) = 0
c
(1s)
B
1
=
1
4
(2 × 1+0× (−1) + 0 × 1+2× (−1)) = 0
c
(1s)
B
2
=
1
4
(2 × 1+0× (−1) + 0 × (−1) + 2 × 1) = 1
⇒ Γ
(1s)
=A
1
⊕ B
2
.
This means that one can therefore construct one linear combination of the two 1s(H) orbitals of H
2
O
with A
1
symmetry (totally symmetric) and one with B
2
symmetry as will be shown in the following.
———————————————————
4.3 Useful applications of group theory
4.3.1 Determination of symmetrized linear combinations of atomic orbitals
To find the symmetrized linear combination of atomic orbitals (LCAO), one uses so-called
projectors
ˆ
P . The projector associated with the irreducible representation Γ is defined by
ˆ
P
Γ
=
1
h
ˆ
O
χ
(Γ)
(
ˆ
O) ×
ˆ
O. (4.11)
The application of
ˆ
P
Γ
onto the atomic orbitals provides a LCAO of symmetry Γ.
PCV - Spectroscopy of atoms and molecules
4.3. USEFUL APPLICATIONS OF GROUP THEORY 115
———————————————————
Example : symmetrized LCAOs of the two 1s orbitals on the H atoms of H
2
O.
ˆ
P
A
1
1s(1) =
1
4
[1 × E 1s(1) + 1 × C
z
2
1s(1) + 1 × σ
xz
1s(1) + 1 × σ
yz
1s(1)]
=
1
4
[1s(1) + 1s(2) + 1s(2) + 1s(1)] =
1
2
[1s(1) + 1s(2)]
ˆ
P
A
2
1s(1) =
1
4
[1 × E 1s(1) + 1 × C
z
2
1s(1) − 1 × σ
xz
1s(1) − 1 × σ
yz
1s(1)]
=
1
4
[1s(1) + 1s(2) − 1s(2) − 1s(1)] = 0
As expected, no A
2
linear combination can be formed from the 1s(H) functions. Similarly one finds
ˆ
P
B
1
1s(1) = 0 , and
ˆ
P
B
2
1s(1) =
1
2
[1s(1) − 1s(2)] .
The two LCAOs of symmetry A
1
and B
2
can be represented schematically in Figure 4.9.
O
H
(2)
H
(1)
O
H
(2)
H
(1)
A symmetry
1
B symmetry
2
Figure 4.9: Linear combinations of atomic orbital 1s(H) of H
2
OofsymmetryA
1
and B
2
.
The symmetrized LCAOs can then be used to determine the chemical bonds that can be formed with
the p orbitals on the O atom. First, one must determine the transformation properties of the p orbitals
on the O atom depicted schematically in Figure 4.10.
O
H
H
O
H
H
H
H
p
z
O
p
y
p
x
x
y
z
Figure 4.10: p orbitals on the O atom.
The p
x
,p
y
,andp
z
orbitals of the O atoms transform like x, y,andz, respectively as indicated in
Section 4.2.2. Hence: Γ
(p
x
)
=B
1
,Γ
(p
y
)
=B
2
,andΓ
(p
z
)
=A
1
as indicated in the third column of the
character table.
Only orbitals of the same symmetry can be combined to form bonding or antibonding molecular
PCV - Spectroscopy of atoms and molecules
116 CHAPTER 4. GROUP THEORY
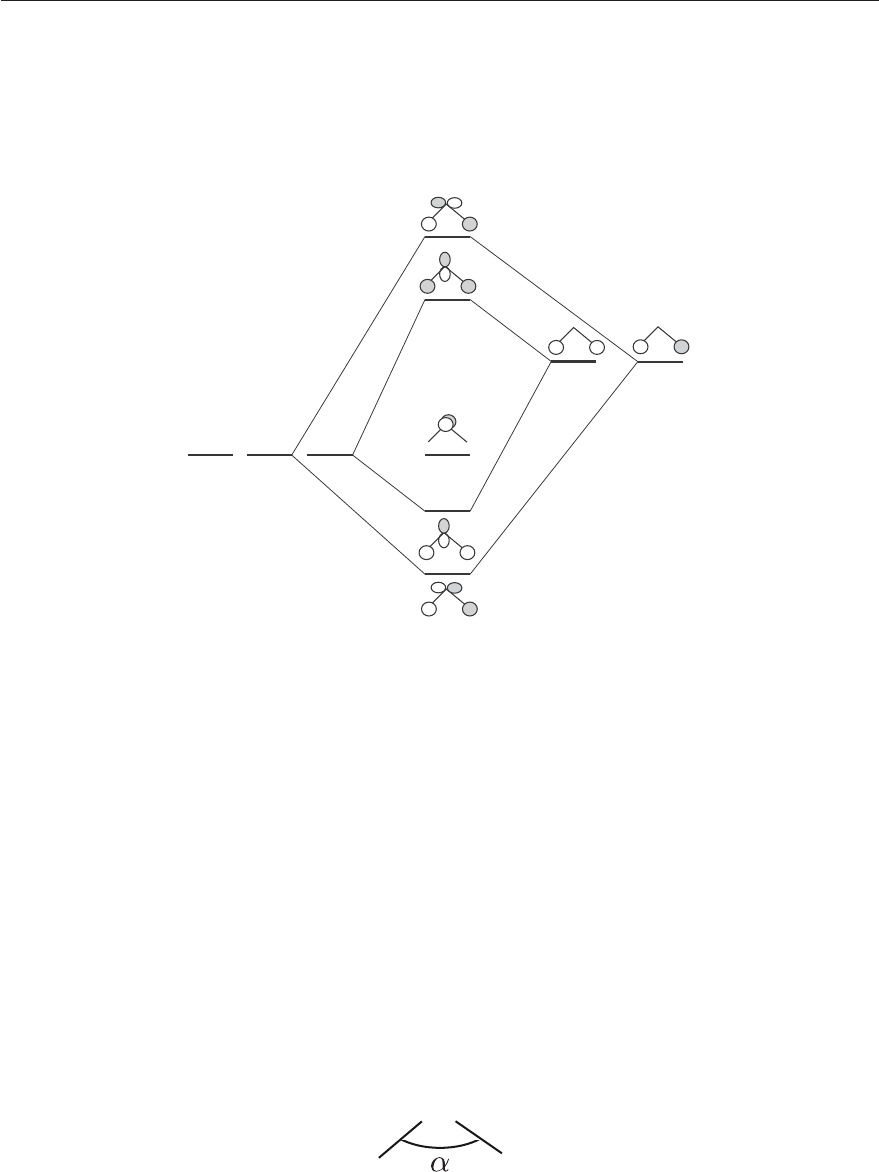
orbitals. The five symmetrized orbitals listed above can be used to form five molecular orbitals
according to the following diagram (Figure 4.11) which does not take the 1s and 2s orbitals on the
oxygen into account because only valence electrons are considered for the formation of chemical bonds.
H
1s
O
2p
p
x
p
y
B
1
B
2
p
z
A
1
b
1
B
2
A
1
a
1
b
2
a
1
b
2
*
*
Figure 4.11: Valence molecular orbitals of H
2
O built from symmetrized H(1s) “ligand” or-
bitals and the 2p atomic orbitals of O. The labels of the molecular orbitals refer to their
symmetry in lower case letters.
From the electronic configuration of each atom, there are six valence electrons (O ... (2p)
4
,H(1s)
1
)
to place in the Molecular Orbitals (MOs) following Pauli’s Aufbau-principle gives the ground state
configuration: ...(b
2
)
2
(a
1
)
2
(b
1
)
2
with an overall symmetry A
1
. Because four of the six electrons are
in bonding orbitals and two in a non bonding p
x
orbital, one expects two chemical bonds in H
2
O.
The energetical ordering of the two bonding MO of B
2
and A
1
symmetry depends on the HOH angle
α defined in Figure 4.12. Whereas the a
1
orbital becomes nonbonding at α = 180
◦
,theb
2
orbital
remains bonding at α = 180
◦
but becomes antibonding at small angles.
Figure 4.12: Bond angle α.
———————————————————
PCV - Spectroscopy of atoms and molecules
4.3. USEFUL APPLICATIONS OF GROUP THEORY 117
4.3.2 Symmetry of normal modes
We consider the 3N-dimensional reducible representation Γ
3N
spanned by the set of 3N
Cartesian coordinates of the N atoms in a molecule and reduce it into irreducible repre-
sentations of the corresponding group. The molecule can also be characterized by its 3N
displacement coordinates i. e. the translations (t), rotations (r) and vibrations (v). There-
fore:
Γ
3N
=Γ
t
⊕ Γ
r
⊕ Γ
v
(4.12)
The representation of the vibrational modes Γ
v
can be deduced from Γ
3N
subtracting the
representations Γ
t
and Γ
r
as indicated in the character table.
———————————————————
Example:
The vibrational modes of H
2
O
The total representation is 3 × 3 = 9-dimensional. All irreducible representations of C
2v
are one-
dimensional, and only three vibrational modes (3N-6) exist in H
2
O. The symmetry of these modes will
be obtained by eliminating the six irreducible representations corresponding to the three translational
and the three rotational degrees of freedom of the molecule.
Figure 4.13: Coordinates used to derive the Γ
9
representation of H
2
OintheC
2v
group.
In the basis set (or representation) Γ
9
= {x
1
,y
1
, ..., z
3
},theC
2v
symmetry operations are represented
by 9 × 9 matrices.
PCV - Spectroscopy of atoms and molecules

118 CHAPTER 4. GROUP THEORY
The matrix representing the identity E is given by:
E
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
x
1
y
1
z
1
x
2
y
2
z
2
x
3
y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
x
1
y
1
z
1
x
2
y
2
z
2
x
3
y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
1 00000000
0 1 0000000
001 000000
0001 00000
00001 0000
000001 000
0000001 00
00000001 0
000000001
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
x
1
y
1
z
1
x
2
y
2
z
2
x
3
y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Hence the character is χ
(Γ
9
)
(E) = 9 (in agreement with the dimension of the representation).
The matrix representing the rotation C
z
2
is given by:
C
z
2
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
x
1
y
1
z
1
x
2
y
2
z
2
x
3
y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
−x
2
−y
2
z
2
−x
1
−y
1
z
1
−x
3
−y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
0 00−10 00 00
0 0 00−10 0 0 0
000 0 0 10 00
−1000 00000
0 −10 0 0 00 00
001000 000
0 000 00-1 00
0 000 000-1 0
0 000 00001
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎜
⎝
x
1
y
1
z
1
x
2
y
2
z
2
x
3
y
3
z
3
⎞
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎟
⎠
Hence the character is χ
(Γ
9
)
(C
2
)=−1.
From the construction of these two matrices we notice that only atoms that are not exchanged by
the symmetry operations can contribute to the character; therefore in the following, we consider the
atoms that are “invariant” by the operation
ˆ
O only to determine χ
(Γ
9
)
(
ˆ
O).
The reflection σ
xz
exchanges the two H atoms so that only the O atom needs to be considered:
σ
xz
x
3
= x
3
; σ
xz
y
3
= −y
3
; σ
xz
z
3
= z
3
⇒ χ
(Γ
9
)
(σ
xz
)=1.
The reflection σ
yz
does not exchange any atom. For each atom, the x coordinate is inverted and the
y and z coordinates are preserved:
σ
xz
x
i
= −x
i
; σ
xz
y
i
= y
i
; σ
xz
z
i
= z
i
⇒ χ
(Γ
9
)
(σ
yz
)=−1+1+1− 1+1+1− 1+1+1=3
PCV - Spectroscopy of atoms and molecules

4.3. USEFUL APPLICATIONS OF GROUP THEORY 119
The reducible 9-dimensional representation is therefore:
C
2v
EC
z
2
σ
xz
σ
yz
A
1
11 1 1=Γ
z
A
2
1 1 -1 -1 =Γ
R
z
B
1
1-1 1 -1=Γ
x
=Γ
R
y
B
2
1-1 -1 1 =Γ
y
=Γ
R
x
Γ
9
9-1 1 3
The Γ
9
representation can then be reduced using the reduction formula of Equation (4.10)):
c
A
1
=
1
4
(9 − 1+1+3)=3
c
A
2
=
1
4
(9 − 1 − 1 − 3) = 1
c
B
1
=
1
4
(9+1+1− 3) = 2
c
B
2
=
1
4
(9 + 1 − 1+3)=3
Γ
9
=3A
1
⊕ A
2
⊕ 2B
1
⊕ 3B
2
.
From these nine irreducible representations, three correspond to translations (Γ
x
=B
1
,Γ
y
=B
2
,
Γ
z
=A
1
) and three correspond to rotations (Γ
R
x
=B
2
,Γ
R
y
=B
1
,Γ
R
z
=A
2
). The remaining three,
namely 2A
1
⊕ B
2
, correspond to the three vibrational modes of H
2
O(3N − 6=3,becauseH
2
Oisa
nonlinear molecule). To determine these modes one can use the projection formula of Equation (4.11).
Let us consider the vibrational mode of symmetry B
2
as an example. In practice it is convenient to
first treat the x, y and z displacements separately and then to combine the x, y,andz motions.
For the x-dimension:
ˆ
P
B
2
x
1
=
1
4
(1Ex
1
− 1C
z
2
x
1
− 1σ
xz
x
1
+1σ
yz
x
1
)
=
1
4
(x
1
+ x
2
− x
2
− x
1
)=0.
The B
2
mode does not involve x-coordinates.
For the y-andz-dimensions:
ˆ
P
B
2
y
1
=
1
4
(1Ey
1
− 1C
z
2
y
1
− 1σ
xz
y
1
+1σ
yz
y
1
)
=
1
4
(y
1
+ y
2
+ y
2
+ y
1
)=
1
2
(y
1
+ y
2
) .
ˆ
P
B
2
z
1
=
1
4
(1Ez
1
− 1C
z
2
z
1
− 1σ
xz
z
1
+1σ
yz
z
1
)
=
1
4
(z
1
− z
2
− z
2
+ z
1
)=
1
2
(z
1
− z
2
) .
The B
2
mode involves both y and z coordinates. Drawing the displacement vectors one obtains a
vectorial representation of the motion of the H atoms in the B
2
mode. The motion of the O atom
PCV - Spectroscopy of atoms and molecules
120 CHAPTER 4. GROUP THEORY
can be estimated in a same way or reconstructed by ensuring that the center of mass of the molecule
remains stationary.
Figure 4.14: Determination of the nuclear motion of the B
2
mode of water.
The mode can be easily identified as the asymmetric stretching mode.
———————————————————
4.3.3 Symmetry of vibrational levels
The nomenclature to label the vibrational states of a polyatomic molecule is
ν
v
1
1
,ν
v
2
2
, ··· ,ν
v
3N−6
3N−6
(4.13)
where ν
i
designate the mode and v
i
the corresponding vibrational quantum number. Usually
only the modes ν
i
for which v
i
= 0 are indicated. The notation
(v
1
,v
2
, ··· ,v
3N−6
) (4.14)
is also often used. For the ordering of the modes, the totally symmetric modes come first
in order of descending frequency, then the modes corresponding to the second irreducible
representation in the character table in order of descending frequency, etc.
To find the overall symmetry of the vibrational wavefunction one must build the direct
product
Γ
vib
=(Γ
ν
1
)
v
1
⊗ (Γ
ν
2
)
v
2
⊗···⊗(Γ
ν
3N−6
)
v
3N−6
. (4.15)
———————————————————
Example: The three vibrational modes of H
2
O ν
1
is the O-H symmetric stretching mode (˜ν
1
=3585 cm
−1
)
of symmetry A
1
, ν
2
is the H-O-H bending mode (˜ν
2
=1885 cm
−1
) of symmetry A
1
and ν
3
is the O-H
asymmetric stretching mode (˜ν
3
=3506 cm
−1
).
We consider the state with v
1
=2,v
2
=1,v
3
= 3. In the first notation, this will correspond to :
PCV - Spectroscopy of atoms and molecules

4.3. USEFUL APPLICATIONS OF GROUP THEORY 121
1
2
2
1
3
3
. In the second notation, it will correspond to (2 1 3). The symmetry of this vibrational state
is:
Γ
vib
(H
2
O, 1
2
2
1
3
3
)=A
1
⊗ A
1
ν
1
⊗ A
1
ν
2
⊗ B
2
⊗ B
2
⊗ B
2
ν
3
=B
2
.
———————————————————
4.3.4 Symmetry of electronic states and labels of configurations
Just as in the case of vibrational wave functions, the overall symmetry of an electronic
wavefunction is obtained from the direct product
Γ
el
=(Γ
1
)
n
1
⊗ (Γ
2
)
n
2
⊗···⊗(Γ
m
)
n
m
, (4.16)
where Γ
i
is the irreducible representation of orbital i and n
i
is the occupation number of
orbital i in the considered configuration. As totally filled subshells are always totally sym-
metric they do not influence the overall symmetry and can be omitted in equation 4.16.
———————————————————
Example: Electronic ground state configuration of H
2
OandH
2
O
+
:
H
2
O: ...
A
1
(b
2
)
2
(a
1
)
2
(b
1
)
2
(see Figure 4.11)
Γ
el
=B
2
⊗ B
2
(b
2
)
2
⊗ A
1
⊗ A
1
(a
1
)
2
⊗ B
1
⊗ B
1
(b
1
)
2
=A
1
Therefore the electronic ground state is labelled
˜
X
1
A
1
H
2
O
+
: ...
A
1
(b
2
)
2
(a
1
)
2
(b
1
)
1
Γ
el
=B
2
⊗ B
2
(b
2
)
2
⊗ A
1
⊗ A
1
(a
1
)
2
⊗ B
1
(b
1
)
1
=B
1
Therefore the electronic ground is labelled
˜
X
+
2
B
1
———————————————————
Example:
Electronic ground state configuration of the borane molecule BH
3
in the D
3h
point group.
Figure 4.15: BH
3
molecule with its coordinate system.
PCV - Spectroscopy of atoms and molecules
122 CHAPTER 4. GROUP THEORY
We follow the same procedure as for H
2
O in section 4.3.1, retain the 2s and 2p orbitals on the B atom
and the 1s orbitals on the H atoms. First, symmetrized “ligand” orbitals are constructed from the H
1s orbitals; then these are combined with the orbitals of the B atom to form bonding and antibonding
orbitals. For the ligand orbitals, a 3D-representation is spanned by the three 1s atomic orbitals on
the H atom.
D
3h
E 2C
3
3C
2
σ
h
2S
3
3σ
v
A
1
111111
A
2
11−11 1−1 R
z
E
2 −102−10x, y
A
1
111−1 −1 −1
A
2
11−1 −1 −11z
E
2 −10−210 R
x
,R
y
Γ
3D
301301
This representation can be reduced using the reduction formula of Equation (4.10):
c
A
1
=
1
12
[3 × 1 × 1+0× 2 × 1+1× 3 × 1+3× 1 × 1+0× 1 × 1+1× 3 × 1] = 1
c
A
2
=
1
12
[3 × 1 × 1+0+1× 3 × (−1) + 3 × 1 × 1+0+1× 3 × (−1)] = 0
c
E
=
1
12
[3 × 1 × 2+0+1× 3 × 0+3× 1 × 2+0+1× 3 × 0]=1
Γ
3D
=A
1
⊕ E
.
Figure 4.16 shows the ligand orbital of A
1
symmetry found by intuition. The ligand orbitals of E
symmetry are found by using the projection formula of Equation (4.11):
ˆ
P
E
1s(1) =
1
12
2 × E 1s(1) − 1 × C
3
1s(1) − 1 × C
2
3
1s(1) + 2 × σ
h
1s(1) − 1 × S
3
1s(1) − 1 × S
2
3
1s(1)
=
1
12
[2 × 1s(1) − 1s(2) − 1s(3) + 2 × 1s(1) − 1s(2) − 1s(3)]
=
1
3
1s(1) −
1
2
[1s(2) + 1s(3)]
.
To find the second orbital of E
symmetry, we can the projector
ˆ
P
E
to the the 1s(2) and 1s(3)
orbitals; we find two further molecular orbitals
1
3
[1s(2) -
1
2
[1s(1) + 1s(3)]] and
1
3
[1s(3) -
1
2
[1s(1) +
1s(2)]]. The three orbitals are linearly dependent. One can use linear algebra to eliminate one of these
three orbitals and to find an orthogonal set of two orbitals of E
symmetry (see Figure 4.16) using the
Gram-Schmidt orthogonalization procedure.
PCV - Spectroscopy of atoms and molecules
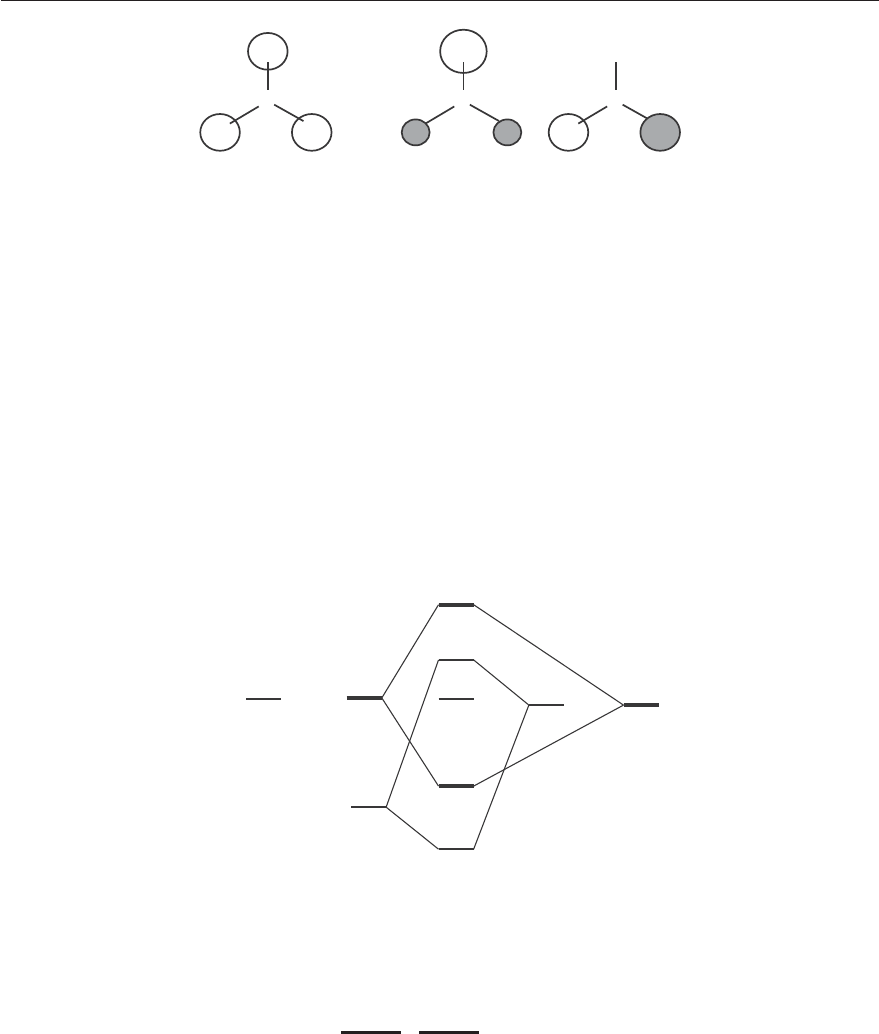
4.3. USEFUL APPLICATIONS OF GROUP THEORY 123
B
H
(1)
H
(2)
H
(3)
B
H
(1)
H
(2)
H
(3)
B
H
(1)
H
(2)
H
(3)
A1’ symmetry E’ symmetry
Figure 4.16: Ligand orbitals of BH
3
.
The molecular orbitals are finally found by determining the symmetry of the 2s and 2p orbitals of
the central B atom and combining the orbitals of the same symmetry into bonding and antibonding
orbitals (see Figure 4.17).
2s(C): A
1
↔ A
1
ligand orbital
p
x
(C), p
y
(C): E
↔ E
ligand orbital
2p
z
(C): A
2
The 2p
z
orbital of A
2
symmetry must remain nonbonding because there are no ligand orbitals of A
2
symmetry.
p
z
2p
x,y
2s
A''
2
E'
2a '
1
1e'
2e'
3a '
1
A'
1
E'
1a ''
2
A'
1
Figure 4.17: Valence molecular orbitals of BH
3
.
The electronic configuration of BH
3
(in total eight electrons) is therefore:
(1a
1
)
2
(2a
1
)
2
(1e
)
4
A
1
(1a
2
)
0
,
where the 1a
1
orbital is the 1s orbital on the B atom. Therefore, the ground state is
˜
X
1
A
1
.
———————————————————
PCV - Spectroscopy of atoms and molecules
124 CHAPTER 4. GROUP THEORY
Example: The case of a linear molecule.
As all homonuclear diatomic molecules, O
2
belongs to the point group D
∞h
. The character table and
direct product tables of D
∞h
are given in Tables 4.3 and 4.4, respectively.
D
∞h
E 2C
ϕ
∞
... ∞σ
v
i 2S
ϕ
∞
... ∞C
2
Σ
+
g
11... 11 1 ... 1 x
2
+ y
2
,z
2
Σ
−
g
11... −11 1 ... −1 R
z
Π
g
22cosϕ... 02−2cosϕ... 0 R
x
,R
y
xz, yz
Δ
g
22cos2ϕ ... 0 2 2 cos 2ϕ... 0 x
2
− y
2
,xy
...
... ... ... ... ... ... ... ...
Σ
+
u
11... 1 −1 −1 ... −1 z
Σ
−
u
11... −1 −1 −1 ... 1
Π
u
22cosϕ... 0 −22cosϕ... 0 x, y
Δ
u
22cos2ϕ ... 0 −2 −2 cos 2ϕ ... 0
... ... ... ... ... ... ... ... ...
Table 4.3: Character table of the D
∞h
point group.
⊗
Σ
+
Σ
−
ΠΔΦ...
Σ
+
Σ
+
Σ
−
ΠΔΦ...
Σ
−
Σ
+
ΠΔΦ...
Π
Σ
+
⊕ Σ
−
⊕ ΔΠ⊕ ΦΔ⊕ Γ ⊕ ...
Δ
Σ
+
⊕ Σ
−
⊕ ΓΠ⊕ H ...
Φ
Σ
+
⊕ Σ
−
⊕ I ...
...
... ... ... ... ... ...
Table 4.4: Direct product table of the point groups C
∞v
and D
∞h
.ForD
∞h
, the “gerade” (g)
or “ungerade” (u) character is determined as follows: g⊗g=u⊗u=gandg⊗u=u⊗g=u.
PCV - Spectroscopy of atoms and molecules

4.3. USEFUL APPLICATIONS OF GROUP THEORY 125
Referring back to Figure 3.10 we can derive the molecular orbitals of O
2
and determine the most
stable electronic configuration to be
(1σ
g
)
2
(1σ
∗
u
)
2
(2σ
g
)
2
(2σ
∗
u
)
2
(3σ
g
)
2
(1π
u
)
4
Σ
+
g
(1π
∗
g
)
2
(3σ
∗
u
)
0
.
All fully occupied orbitals contribute the totally symmetric representation Σ
+
g
to the electronic sym-
metry. The irreducible representations of the electronic states resulting from the above configuration
can be determined from the direct product
Π
g
⊗ Π
g
=Σ
g
⊕
Σ
−
g
⊕ Δ
g
.
Σ
−
g
appearsinsquarebracketsbecauseitistheanti-symmetric part of the direct product, whereas
Σ
g
⊕ Δ
g
is the symmetric part. Since the total electron wave function must be antisymmetric under
exchange of two electrons, the anti-symmetric spatial part combines with the symmetric spin part
giving rise to the
3
Σ
−
g
state, whereas the symmetric spatial part combines with the anti-symmetric
spin part giving
1
Σ
+
g
and
1
Δ
g
states.
———————————————————
4.3.5 Generalized Pauli principle and allowed states
The simplistic expression of the Pauli principle states that two electrons can not occupy the
same spin-orbital. In Section 2.1, we have seen that the wavefunction describing fermions
(particle with half integer spin) must be antisymmetric with respect to the permutation of
two particles, while the wavefunction describing bosons (particle with integer spin) must be
symmetric.
The generalized form of the Pauli principle states that the total wavefunction describing a
molecular system must transform under the group operations
ˆ
O
j
as the irreducible represen-
tation whose characters χ
irr
(
ˆ
O
j
) are given by
χ
irr
(
ˆ
O
j
)=
N
F
i
(−1)
P
i
(
ˆ
O
j
)
(4.17)
where N
F
is the number of types of identical fermions in the system. P
i
(
ˆ
O
j
) is the so-called
parity of the permutation of the i-th kind of fermions.
If the operation
ˆ
O
j
applies on bosons, then χ
irr
(
ˆ
O
j
)=+1.
If the operation
ˆ
O
j
applies on fermions, the parity is “even” (respectively “odd”) if
ˆ
O
j
can
be written as an even (resp. odd) number of permutations (nm). Therefore, χ
irr
(
ˆ
O
j
)=+1
if the permutation of fermions has an even parity and χ
irr
(
ˆ
O
j
)=−1 if the permutation of
PCV - Spectroscopy of atoms and molecules

126 CHAPTER 4. GROUP THEORY
fermions has an odd parity.
———————————————————
Example: the two fermions H
+
in H
2
O
The (1 2) permutation has an odd parity. Hence χ
irr
(1 2) = −1. In the C
2v
group, the operation that
corresponds to the permutation (1 2) is C
z
2
. Two irreducible representations exhibit χ
irr
(C
z
2
)=−1:
B
1
and B
2
.
The total wavefunction of water must transform as B
1
or B
2
. In the Born-Oppenheimer approxima-
tion, the total wavefunction can be written in the product form Ψ
tot
= Φ
el
Φ
vib
Φ
rot
Φ
ns
Φ
es
and its
symmetry can be determined by the direct product
Γ
tot
=Γ
el
⊗ Γ
vib
⊗ Γ
rot
⊗ Γ
ns
⊗ Γ
es
.
Since Γ
el
=A
1
and Γ
vib
=A
1
in the vibrational and electronic ground state, it imposes Γ
rot
⊗ Γ
ns
=
B
1/2
. This shows that not all combinations of rotational levels and nuclear spins are allowed.
———————————————————
Example: CO
2
in the D
∞h
In that case, all operations
ˆ
O
j
apply on bosons only, hence χ
irr
(
ˆ
O
j
) = +1. The total wavefunction
Φ
el
Φ
vib
Φ
rot
should transform as Σ
+
g
.
The vibronic (vibrational-electronic) ground state
:Γ
el
=Σ
+
g
and Γ
vib
=Σ
+
g
.
The rotational wavefunction must transform as Σ
+
g
.
It can be shown that for the CO
2
molecule in a rigid rotor approximation, the even values of J are
associated with rotational wavefunctions of Σ
+
g
symmetry, while the odd values of J are associated
with rotational wavefunctions of Σ
+
u
symmetry. Therefore only half of the rotational levels, with even
values of J (J =0, 2, 4...) are allowed in the electronic vibrational ground state.
The antisymmetric CO stretching ν
3
vibrational state: by applying the protocol described in Sec-
tion 4.3.2, one can find that Γ
ν
3
=Σ
+
u
. In that case, the rotational wavefunction must transform as
Σ
+
u
. Therefore only half of the rotational levels, with odd values of J (J =1, 3, 5...) are allowed in the
ν
3
vibrational state.
Rovibrational transitions (0 0 1)←(0 0 0) fulfil ΔJ = ±1, which in the spectrum gives rise to a P and
an R branches. But every other line is absent compared to the spectrum of CO shown in Figure 3.11
because of the missing states.
It can be shown that for an electronic transition to an electronic state of Π symmetry, this does not
hold and all J values are allowed.
———————————————————
PCV - Spectroscopy of atoms and molecules
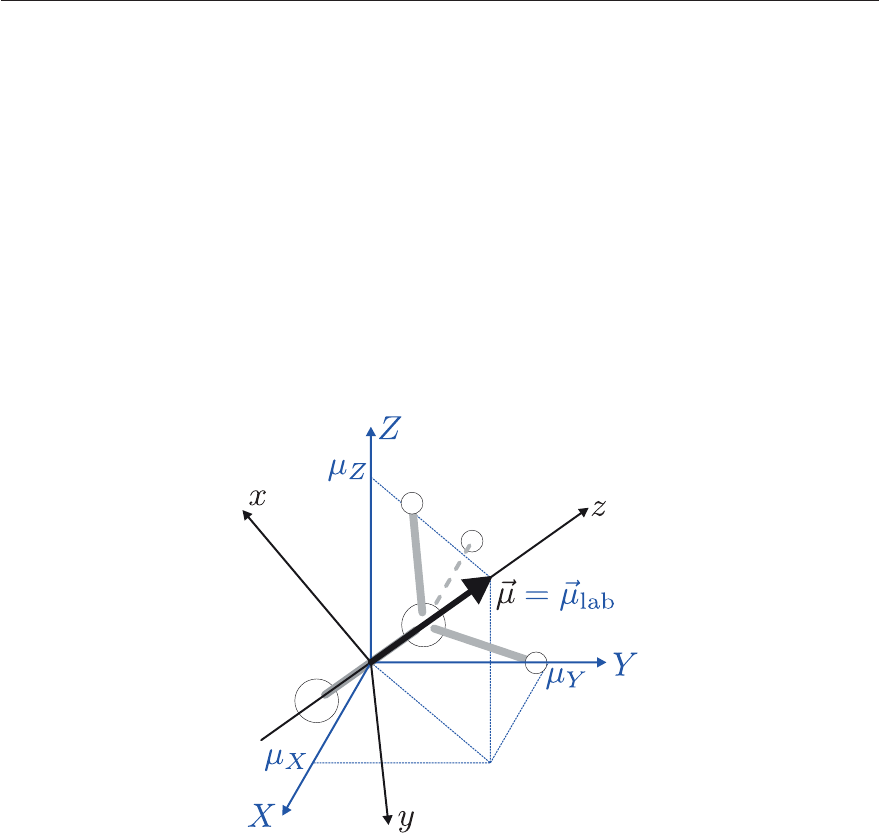
4.3. USEFUL APPLICATIONS OF GROUP THEORY 127
4.3.6 Selection rules with group theory
In the dipole approximation, the interaction between molecules and electromagnetic radiation
is assumed to only come from the interaction
ˆ
V = −
ˆ
μ
lab
·
E. (4.18)
μ
lab
is used here to distinguish the dipole moment of the molecule in the laboratory-fixed
frame from μ, which is the dipole moment in the molecule-fixed frame as illustrated in Fig-
ure 4.18 in the case of the CH
3
Cl molecule.
Figure 4.18: Relationship between the expression of the dipole moment μ =(μ
x
,μ
y
,μ
z
), ex-
pressed in the molecule-fixed reference frame (x, y, z), and that μ
lab
=(μ
X
,μ
Y
,μ
Z
) expressed
in the space-fixed (X, Y, Z) reference frame for CH
3
Cl; the permanent dipole-moment vector
μ lies along the z axis of the molecule-fixed reference frame.
The polarization vector
E of the radiation is defined in the laboratory-fixed frame (X, Y, Z),
whereas the components of μ are defined in the molecule-fixed frame (x, y, z) as follows:
μ
ξ
=
N
i=1
q
i
ξ
i
with ξ = x, y, z and q
i
is the charge of particle i. The space-fixed components μ
X
, μ
X
,and
μ
Z
of μ
lab
vary as the molecule rotates while the molecule-fixed components μ
x
, μ
y
,andμ
z
remain the same.
PCV - Spectroscopy of atoms and molecules

128 CHAPTER 4. GROUP THEORY
For a linearly polarized light
E =(0, 0,E),
ˆ
V = −ˆμ
Z
E. (4.19)
As the intensity of an electric dipole transition between an initial state Ψ
i
and a final state
Ψ
f
is proportional to Ψ
f
|
ˆ
V |Ψ
i
, the selection rule can be written as follows:
Ψ
f
|ˆμ
Z
|Ψ
i
=0. (4.20)
The wavefunctions Ψ
i
and Ψ
f
are expressed in the molecule-fixed frame (x, y, z); for simplicity,
the selection rules are usually expressed in terms of μ
x
, μ
y
,andμ
z
instead of μ
X
, μ
Y
,and
μ
Z
. Therefore one needs to express μ
X
, μ
Y
,andμ
Z
as functions of μ
x
, μ
y
,andμ
z
i. e. the
transformation from the space-fixed frame to the molecule-fixed frame.
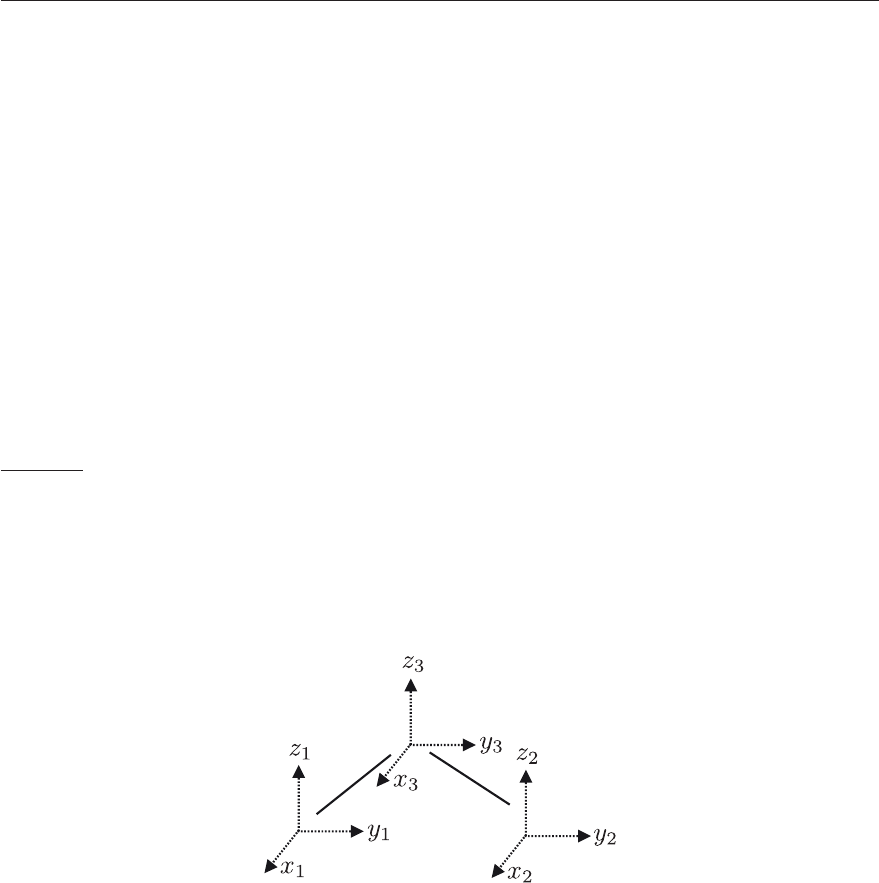
The relative orientation of the space-fixed and molecule-fixed coordinate systems is given by
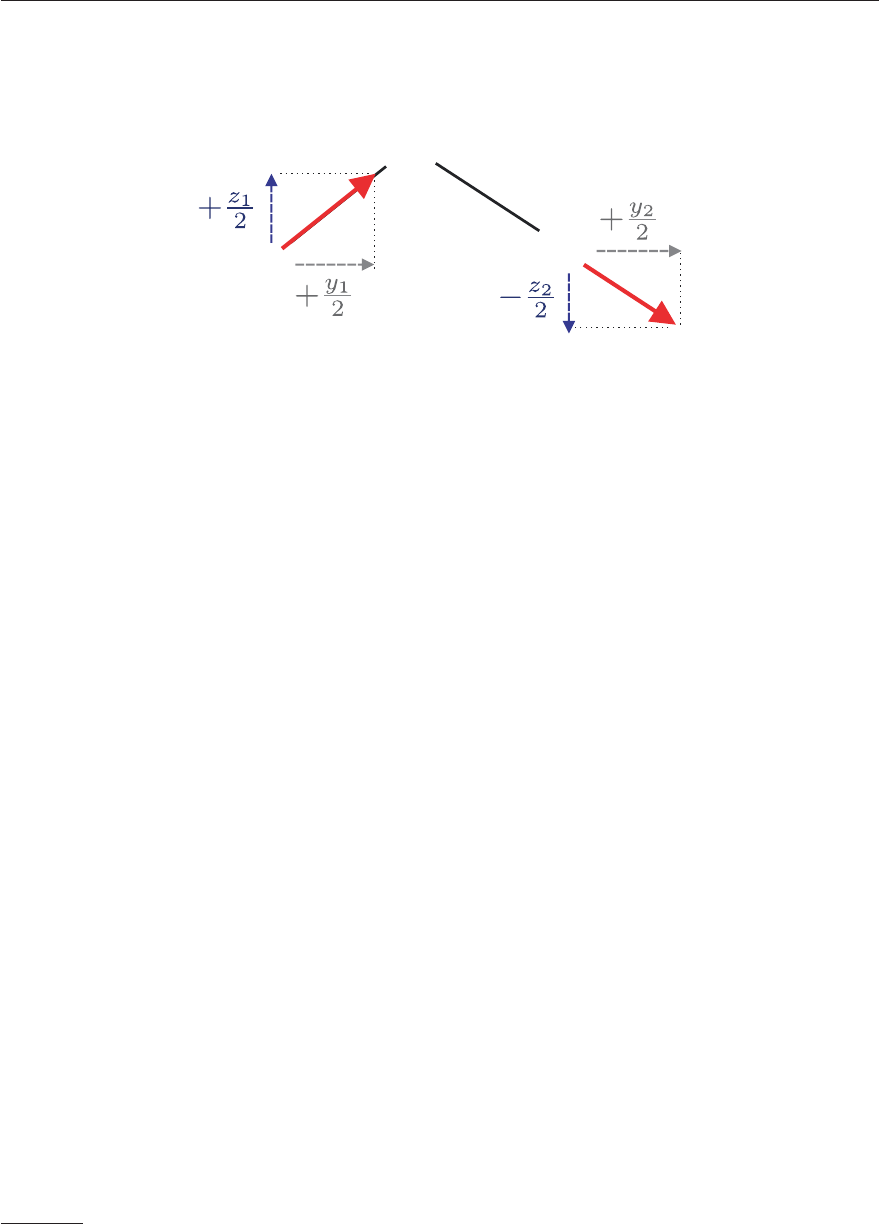
the three Euler angles (ϕ, θ, χ) defined by three successive rotations depicted in Figure 4.19:
1. the rotation around Z by ϕ which generates the coordinate system (x
,y
,z
)ingreyin
Figure 4.19
2. the rotation around y
by θ which generates the coordinate system (x
,y
,z
)inredin
Figure 4.19
3. the rotation around z
by χ which generates the coordinate system (x, y, z) in black in
Figure 4.19.
The transformation 1 can be written as follows:
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
= R
Z
(ϕ)
⎛
⎜
⎜
⎜
⎜
⎜
⎝
X
Y
Z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
cos ϕ sin ϕ 0
−sin ϕ cos ϕ 0
001
⎞
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎝
X
Y
Z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
(4.21)
The transformation 2 can be written as follows:
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
= R
y
(θ)
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
cos θ 0 −sin θ
01 0
sin θ 0cosθ
⎞
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
(4.22)
The transformation 3 can be written as follows:
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
= R
z
(χ)
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
=
⎛
⎜
⎜
⎜
⎜
⎜
⎝
cos χ sin χ 0
−sin χ cos χ 0
001
⎞
⎟
⎟
⎟
⎟
⎟
⎠
⎛
⎜
⎜
⎜
⎜
⎜
⎝
x
y
z
⎞
⎟
⎟
⎟
⎟
⎟
⎠
(4.23)
PCV - Spectroscopy of atoms and molecules
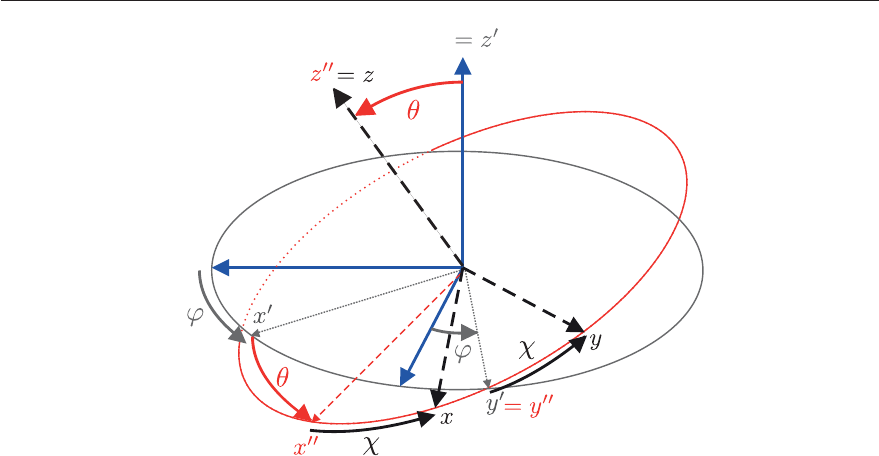
4.3. USEFUL APPLICATIONS OF GROUP THEORY 129
Figure 4.19: Euler angles θ, φ, χ defining the relative orientation of the space-fixed reference
frame (X, Y, Z) in blue and the molecule-fixed reference frame (x, y, z) in black. Starting from
the space-fixed reference frame, the molecule-fixed reference frame is obtained by 1) rotation
by an angle ϕ around the Z axis, leading to the intermediate (x
,y
,z
in grey) frame; 2)
rotation by an angle θ around the y
axis, leading to the second intermediate (x
,y
,z
in
red) frame; and 3) rotation by an angle χ around the z
axis.
Using these three equations, the laboratory- and molecule-fixed frames can be linked by the
following transformation:
⎡
⎢
⎢
⎢
⎢
⎣
x
y
z
⎤
⎥
⎥
⎥
⎥
⎦
= R
z
(χ)R
y
(θ)R
Z
(ϕ)
⎡
⎢
⎢
⎢
⎢
⎣
X
Y
Z
⎤
⎥
⎥
⎥
⎥
⎦
(4.24)
=
⎡
⎢
⎢
⎢
⎢
⎣
cos ϕ cos θ cos χ − sin ϕ sin χ sin ϕ cos θ cos χ +cosϕ sin χ −sin θ cos χ
−cos ϕ cos θ sin χ − sin ϕ cos χ −sin ϕ cos θ sin χ +cosϕ cos χ sin θ sin χ
cos ϕ sin θ sin ϕ sin θ cos θ
⎤
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎣
X
Y
Z
⎤
⎥
⎥
⎥
⎥
⎦
PCV - Spectroscopy of atoms and molecules

130 CHAPTER 4. GROUP THEORY
or its inverse
⎡
⎢
⎢
⎢
⎢
⎣
X
Y
Z
⎤
⎥
⎥
⎥
⎥
⎦
=
⎡
⎢
⎢
⎢
⎢
⎣
cos ϕ cos θ cos χ − sin ϕ sin χ −cos ϕ cos θ sin χ − sin ϕ cos χ cos ϕ sin θ
sin ϕ cos θ cos χ +cosϕ sin χ −sin ϕ cos θ sin χ +cosϕ cos χ sin ϕ sin θ
−sin θ cos χ sin θ sin χ cos θ
⎤
⎥
⎥
⎥
⎥
⎦
⎡
⎢
⎢
⎢
⎢
⎣
x
y
z
⎤
⎥
⎥
⎥
⎥
⎦
=
λ
⎡
⎢
⎢
⎢
⎢
⎣
x
y
z
⎤
⎥
⎥
⎥
⎥
⎦
, (4.25)
where λ is the direction cosine matrix. λ can thus be used to express the components of a vector in
the laboratory-fixed frame as a function of the components of the same vector in the molecule-fixed
frame, and especially μ
Z
as a function of μ
x
, μ
y
,andμ
z
:
μ
Z
= λ
Zx
μ
x
+ λ
Zy
μ
y
+ λ
Zz
μ
z
. (4.26)
In the Born-Oppenheimer approximation, the molecular wavefunctions Ψ
f
and Ψ
i
are expressed in the
product form
Ψ
f
= φ
el
φ
vib
φ
rot
φ
nspin
φ
espin
, and (4.27)
Ψ
i
= φ
el
φ
vib
φ
rot
φ
nspin
φ
espin
. (4.28)
The transition moment Ψ
f
|ˆμ
Z
|Ψ
i
cannowbewrittenasfollows:
φ
el
φ
vib
φ
rot
φ
nspin
φ
espin
|
α
λ
Zα
ˆμ
α
|φ
el
φ
vib
φ
rot
φ
nspin
φ
espin
. (4.29)
Equations (4.20) and (4.29) lead to the selection rules for an electric dipole transition.
Spin conservation upon electric dipole transition
The φ
nspin
functions depend on the nuclear spin variables only, and the φ
espin
functions depend on
the electron spin variables only. Their integration in Equation (4.29) can thus be separated:
φ
espin
|φ
espin
φ
nspin
|φ
nspin
φ
el
φ
vib
φ
rot
|
α
λ
Zα
ˆμ
α
|φ
el
φ
vib
φ
rot
. (4.30)
Because electron- and nuclear-spin functions are orthogonal, Equation (4.30) vanishes (transition
forbidden) unless φ
espin
= φ
espin
and φ
nspin
= φ
nspin
, which bring the selection rules:
• ΔS =0 interdiction of intercombination
• ΔI =0 nuclear-spin conservation rule
PCV - Spectroscopy of atoms and molecules

4.3. USEFUL APPLICATIONS OF GROUP THEORY 131
Angular momentum selection rules
The remaining rovibronic (rotational-vibrational-electronic) transition moment in Equation (4.30)
φ
el
φ
vib
φ
rot
|
α
λ
Zα
μ
α
|φ
el
φ
vib
φ
rot
can be further simplified.
A rotation of the molecule in space leads to a change of the Euler angles, and the rotational wave-
functions φ
rot
(ϕ, θ, χ) are expressed in the space-fixed frame as a function of these angles, while the
functions φ
el
, φ
vib
and μ
α
do not depend on the Euler angles: φ
el
(q
i
,Q), φ
vib
(Q), μ
α
(q
i
,Q). The
direction cosine elements λ
Zα
and φ
rot
only depend on ϕ, θ, χ and the integration can be further
separated in an integral over angular variables and an integral over electronic coordinates and normal
modes:
α
φ
rot
|λ
Zα
|φ
rot
φ
el
φ
vib
|ˆμ
α
|φ
el
φ
vib
. (4.31)
The integral φ
rot
|λ
Zα
|φ
rot
leads to angular momentum selection rules:
• ΔJ =0, ±1; 0 ↔ 0 angular momentum conservation (see also Chapter 2)
The projection quantum number M of J on the Z axis leads to further selection rules:
• if the polarization is along the Z axis, then ΔM =0
• if the polarization is along the X or Y axis, then ΔM = ±1
Finally,
• if the dipole moment lies on the z axis, the transition is said parallel and ΔΛ =0fordiatomic
molecules
• if the dipole moment lies on the x or y axis, the transition is said perpendicular and ΔΛ = ±1
for diatomic molecules
Further selection rules
The integral φ
el
φ
vib
|ˆμ
α
|φ
el
φ
vib
of Equation (4.31) represents a selection rule for transitions between
electronic and vibrational levels. Depending of the type of transitions investigated, its evaluation can
be simplified using the vanishing integral theorem and group theory: this theorem states that the
product Ψ
2
|
ˆ
O|Ψ
1
vanishes if the product of the symmetry representation of Ψ
∗
2
,
ˆ
O and Ψ
1
does not
contain the totally symmetric irreducible representation Γ
(sym)
irr
of the group, i. e.
Ψ
2
|
ˆ
O|Ψ
1
=0⇒ Γ(Ψ
∗
2
) ⊗ Γ(
ˆ
O) ⊗ Γ(Ψ
1
) ⊃ Γ
(sym)
irr
(4.32)
This theorem will be used in three cases in the following.
Rotational spectroscopy: φ
el
= φ
el
, φ
vib
= φ
vib
The integral φ
el
φ
vib
|ˆμ
α
|φ
el
φ
vib
of Equation (4.31) represents the expectation value of ˆμ
α
.Tran-
sitions are only allowed for molecules with a permanent dipole moment. The angular momentum
selection rules are as above.
PCV - Spectroscopy of atoms and molecules

132 CHAPTER 4. GROUP THEORY
Vibrational spectroscopy: φ
el
= φ
el
, φ
vib
= φ
vib
Since, in the BO approximation, only φ
el
and μ
α
depend on electron coordinates q
i
, the integration
over q
i
can be done first:
φ
vib
(Q)|φ
el
(Q, q
i
)|ˆμ
α
(Q, q
i
)|φ
el
(Q, q
i
)
q
i
ˆμ
el,α
(Q)
|φ
vib
(Q)
Q
= φ
vib
(Q)|ˆμ
el,α
(Q)|φ
vib
(Q). (4.33)
Whether Equation (4.33) vanishes or not, can be determined using the vanishing integral theorem.
Therefore the transition is allowed if
Γ
vib
⊗ Γ
α
⊗ Γ
vib
⊃ Γ
(sym)
irr
, (4.34)
where Γ
α
(α = x, y, z) transforms as the components of a vector and thus as α.
———————————————————
Example:
the case of H
2
O
The vibrational ground state φ
vib
= (0,0,0) has the symmetry Γ
vib
=A
1
The components of the dipole moment have the symmetries Γ
μ
x
=B
1
,Γ
μ
y
=B
2
,andΓ
μ
z
=A
1
.
The vibrational state φ
vib
= (1,0,0) has the symmetry Γ
vib
=A
1
.
Γ
vib
⊗ Γ
α
⊗ Γ
vib
=A
1
⊗
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⊗ A
1
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
The allowed vibrational transition originates from the z component of the transition dipole moment.
The vibrational φ
vib
= (0,0,1) has the symmetry Γ
vib
=B
2
.
B
2
⊗
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⊗ A
1
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
A
2
A
1
B
2
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
The allowed vibrational transition originates here from the y component of the transition dipole
moment. The component of the permanent dipole moment along the y axis is zero in H
2
O. Nevertheless
a transition can be observed. The condition for a vibrational transition to be observable is that a
change of the dipole moment must occur when exciting the vibration. This is obviously the case when
the antisymmetric stretching mode is excited in H
2
O.
One can show that transitions to all vibrational levels are allowed by symmetry in H
2
O. However,
overtones are weaker than fundamental excitations as discussed in the case of diatomic molecules in
Section 3.5.1.
———————————————————
PCV - Spectroscopy of atoms and molecules

4.3. USEFUL APPLICATIONS OF GROUP THEORY 133
Electronic spectroscopy: φ
el
= φ
el
The left hand side of Equation (4.33) can be written as
φ
vib
(Q)|φ
el
(Q, q
i
)|ˆμ
α
(Q, q
i
)|φ
el
(Q, q
i
)
q
i
μ
fi
el,α
|φ
vib
(Q)
Q
, (4.35)
where the inner integral represents an electronic transition moment μ
fi
el,α
obtained by inte-
gration over the electronic coordinates.
A transition is electronically allowed when μ
fi
el,α
= 0, which is fulfilled if
Γ
el
⊗ Γ
α
⊗ Γ
el
⊃ Γ
(sym)
irr
. (4.36)
———————————————————
Example:
the case of H
2
O
The electronic ground state is
˜
X
1
A
1
Γ
el
⊗ Γ
α
⊗ Γ
el
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⊗
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⊗ A
1
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
A
1
A
1
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
Electric dipole transitions to electronic states of B
1
,B
2
and A
1
symmetry are electronically allowed
and transitions to electronic states of A
2
symmetry are electronically forbidden in H
2
O.
———————————————————
If one assumes that the transition moment function μ
fi
el,α
(Q) varies slowly with Q,then
μ
fi
el,α
(Q) can be described by a Taylor series and one can in good approximation neglect
higher terms:
μ
fi
el,α
(Q)=
$
μ
fi
el,α
%
eq
+
3N−6
j
&
∂μ
fi
el,α
∂Q
j
'
eq
Q
j
+ ... (4.37)
In electronically allowed transitions the first term in Equation (4.37) is often the dominant
one and the transition moment (Equation (4.35)) becomes:
φ
vib
(Q)|φ
vib
(Q)
$
μ
fi
el,α
%
eq
. (4.38)
The intensity of a transition is proportional to the square of the transition moment and thus,
I ∝
(
(
φ
vib
(Q)|φ
vib
(Q)
(
(
2
. (4.39)
|φ
vib
(Q)|φ
vib
(Q)|
2
is called a Franck-Condon factor and represents the square of the
overlap of the vibrational wavefunctions. Equation (4.39) implies the vibrational selection
rule for electronically allowed transitions:
Γ
vib
⊗ Γ
vib
⊃ Γ
(sym)
irr
. (4.40)
PCV - Spectroscopy of atoms and molecules

134 CHAPTER 4. GROUP THEORY
———————————————————
Example: H
2
O
˜
X
1
A
1
(0, 0, 0) → H
2
O
˜
C
1
B
1
Γ
vib
=A
1
⇒ Γ
vib
!
=A
1
Only the symmetric stretching mode ν
1
and the bending mode ν
2
can be excited. The asymmetric
stretching mode ν
3
of B
2
symmetry can only be excited if v
3
is even.
———————————————————
Electronically forbidden transitions can become weakly allowed if the electronic and vibra-
tional degrees of freedom cannot be separated as in Equation (4.35). The condition for them
to be weakly observable is that
Γ
vib
⊗ Γ
el
Γ
ev
⊗ Γ
α
⊗ Γ
vib
⊗ Γ
el
Γ
ev
⊃ A
1
. (4.41)
———————————————————
Example:
Transitions from H
2
O
˜
X
1
A
1
(0,0,0) to electronically excited states of A
2
symmetry (electronically
forbidden) may become weakly allowed (vibronically allowed) if a non totally symmetric mode is ex-
cited.
˜
X
1
A
1
(0,0,0): Γ
el
=A
1
,Γ
vib
=A
1
,Γ
ev
=A
1
⊗ A
1
=A
1
A
2
(0,0,1): Γ
el
=A
2
,Γ
vib
=B
2
,Γ
ev
=A
2
⊗ B
2
=B
1
Γ
ev
⊗ Γ
α
⊗ Γ
ev
=B
1
⊗
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
B
1
B
2
A
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
⊗ A
1
=
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
A
1
A
2
B
1
⎫
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎭
The vibronically allowed transition originates from μ
x
.
———————————————————
PCV - Spectroscopy of atoms and molecules
