1
Reciprocal Space Mapping for Dummies
Samuele Lilliu
1
, Thomas Dane
2
1
University of Sheffield, Hicks Building, Hounsfield Road, Sheffield, S3 7RH (UK),
2
European Synchrotron Radiation Facility,
BP 220, Grenoble F-38043, France.
Abstract
Grazing Incidence X-ray Diffraction (GIXD) is a surface sensitive X-ray investigation technique (or
geometry configuration) that can reveal the structural properties of a film deposited on a flat
substrate
1-4
. The term grazing indicates that the angle between the incident beam and the film is small
(typically below 0.5°). This essential technique has been employed on liquid crystals
5,6
, nanoparticles
and colloids
7,8
, nanostructures
9
, corrosion processes
10,11
, polymers
12-14
, bio-materials
15-17
,
interfaces
11,18
, materials for solar cells
19-25
, photodiodes
26
, and transistors
27,28
, etc. Diffraction patterns
in GIXD geometry are typically captured with a 2D detector, which outputs images in pixel coordinates.
A step required to perform analyses such as grain size estimation, disorder, preferred orientation,
quantitative phase analysis of the probed film surface, etc.
29
, consists in converting the diffraction
image from pixel coordinates to the momentum transfer or scattering vector in sample coordinates
(the ‘reciprocal space mapping’)
30
. This momentum transfer embeds information on the crystal or
polycrystal and its intrinsic rotation with respect to the substrate. In this work we derive, in a rigorous
way, the reciprocal space mapping equations for a ‘3D+1S’ diffractometer in a way that is
understandable to anyone with basic notions of linear algebra, geometry, and X-ray diffraction.
Introduction
Two-dimensional X-ray diffraction (XRD
2
) is a well-established technique in the field of X-ray diffraction
(XRD)
29
. The main complication of data analysis in XRD
2
compared to one dimension XRD is the
remapping of detector pixel coordinates into momentum transfer or scattering vector coordinates.
The geometry of a two-dimensional X-ray diffraction system consists of three reference systems:
laboratory, detector, and sample. The laboratory coordinate system is the reference or global three
dimensional coordinate system. The sample coordinate system shares the same origin with the
laboratory system but its basis can be oriented in a different way. The detector coordinates system is
two-dimensional. The three reference systems are represented by orthogonal Cartesian basis
31-34
.
In this work we employ a ‘3D+1S’ diffractometer, where three diffractometer circles (3D) are used
for moving the 2D detector across the Ewald sphere, and one circle is used for orienting the sample.
The simplest detector orientation corresponds to the situation in which the normal to the detector is
coincident to the X-ray incident beam or, equivalently, points towards the origin of the laboratory
coordinate system, where the sample is placed (detector circle angles are zero). The simplest sample
orientation corresponds to the grazing case in which the sample surface is parallel to the direct beam
(sample circle angle is zero). Let’s assume that our sample is a powder of randomly oriented crystals
and consider a diffracting plane. The diffracting plane would project a cone of rays (Debye-Scherrer
ring) onto the detector
1
. Since the detector is perpendicular to incident beam and the sample is
parallel to the incident beam, the projection of the diffracting cone onto the detector would be a
perfect circle. In this case, converting detector’s pixel coordinates into scattering vector coordinates
is non-trivial. However, one might want to move the detector to non-zero azimuth and elevation to
visualize extra Debye-Scherrer rings. This complicates things and introduces distortions in the
diffraction pattern. In the most general case the Debye-Scherrer rings will have a tilted ellipse shape,
which result from the intersection of the diffracting cone with the tilted detector plane. In this case,
the conversion between pixels and scattering vector coordinates is more complicated.
2
We start our discussion by introducing the diffractometer geometry and the laboratory coordinate
system. We then show how to construct the rotation matrices for the detector rotation (3D). The next
step is to project a ray with the same direction of the exit wave versor
onto a rotated detector. The
projected ray is converted into the two-dimensional detector coordinates. At this point we have a set
of equations that convert the exit wave versor ray into an image point. These equations can be
inverted so that, given an image point, we can retrieve the ray information. We then introduce the
effect of the rotation of one sample circle and derive the equations required to reconstruct the
scattering vector in sample coordinates, which contains information on the crystal and its intrinsic
rotation with respect to the substrate.
Diffractometer Geometry and Laboratory System
For simplicity we refer to a common synchrotron beamline setup, such as the one employed at the
XMaS beamline (BM28, the European Synchrotron, ESRF)
35
, even though the following discussion can
be applied to similar configurations. As shown in Figure 1a-b, a chamber with a sample holder is
mounted on a 12 circle Huber diffractometer, placing the sample at the origin of the laboratory and
sample coordinate system.
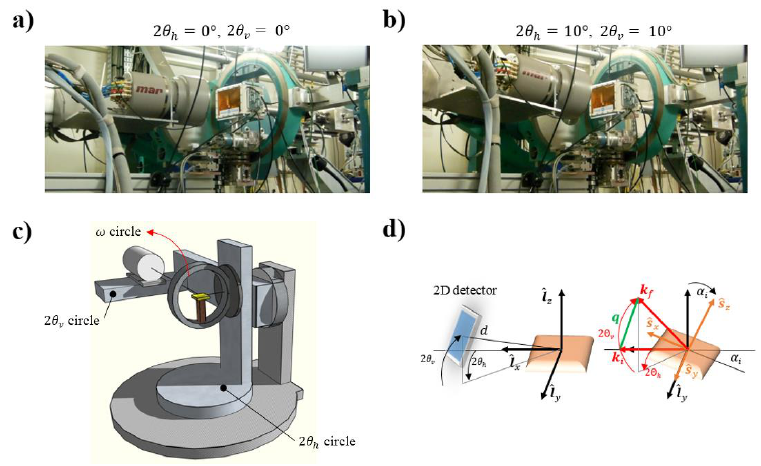
Figure 1 - Diffractometer Geometry. a) Detector at the ‘origin’ position with
and
. b) Detector
at
and
. c) Diffractometer sketch. d) Laboratory (
and sample (
)
coordinate systems; with the blue rectangle representing the detector ( is the sample-detector distance,
and
are the detector angular coordinates, is an extra motor that spins the detector about its normal) and
the orange rectangle representing the sample. The sample in the second picture of d) is tilted of an out-of-plane
incident angle
. The incident wave vector (direct X-ray beam) is
and the diffracted wave vector is
, with
and
being its angular coordinates. The scattering vector is
. Wave vectors and scattering
vector are discussed later in the text.
Here we consider two detector circles (
and
) and one sample pitch circle (
). We also add an
extra degree of freedom for the detector though a third detector circle , which rotates the detector
about its normal. The diffractometer geometry is depicted in Figure 1d.
3
The global coordinate system (or laboratory) coordinate (or reference) system is the standard
orthogonal Cartesian basis with origin at the diffractometer centre :
(1)
where
are unit vectors (versors), and is the identity matrix
31-34
. The horizontal detector circle
moves the detector counterclockwise with respect to
for
(see Figure 1d). The vertical
detector circle moves the detector clockwise (upwards) with respect to the
axis for
(when
). An out-of-plane incidence angle or pitch
moves the sample clockwise with respect
to
. The extra detector circle is not installed at the XMaS beamline, but could be used to rotate
counterclockwise the detector about its normal allowing combined grazing incidence wide angle x-ray
scattering (GIWAXS) and grazing incidence small angle x-ray scattering (GISAXS) for example
36
.
Tracking the Detector Movement
For simplicity we assume that the detector has a square shape. Given a fixed point on the detector
(e.g. its top-right corner), we would like to know the location of this point in the laboratory system
when the
,
, and circle angles are non-zero. This can be done by constructing a rotation
matrix that will rotate the point . When constructing the rotation matrix we need to pay attention
to the way the circles are mounted. In our case the circle is mounted on the
circle, which is
mounted on the
circle (Figure 1c). The way to build the total rotation matrix proceeds from the
inner circle to the outer circle as
30
. The following calculations can be
performed in MATLAB with Script 2, Supplementary Information.
The first rotation matrix
is counterclockwise
31-34
with respect to
and
represents the detector rotation about its normal:
(2)
The second rotation matrix
is counterclockwise about
(or clockwise about
)
and represents the
detector rotation in the vertical direction (elevation):
(3)
Note again that the convention used here is that a positive
rotation is clockwise about
, while
in ref.
36
a positive
rotation corresponds to a counterclockwise rotation about
.
The last rotation matrix
is counterclockwise about
and represents the
detector rotation in the horizontal direction (azimuth):
(4)
4
The total rotation matrix is:
(5)
With this rotation, the standard basis versors
rotate and the rotated basis becomes
. The rotated point ’, expressed in the basis (and not in the
basis) is located
at:
(6)
Note that
do not commute
37
. The matrix
represents an orthogonal (
) and
rigid transformation, which preserves the orientation of the transformed vectors (
).
When eq. (5) reduces to:
(7)
Projecting the Exit Wave Vector onto the Detector
We define
as the incident wave vector from the X-ray direct beam and
as the scattered or
diffracted (exit) wave vector (Figure 1d). The type of scattering considered here is due to the
absorption of incident radiation with subsequent re-emission (elastic scattering)
where is the wavelength. Generally speaking, when the direct beam hits a
crystalline sample, a diffracting ray is irradiated from the sample itself. The ray direction is given by
the direction of the exit wave versor
. The angle between the incident and the exit vector
is the Bragg angle and their difference is the scattering vector
. The exit wave vector
describes a sphere of radius called the Ewald sphere. More details on X-ray diffraction can be
found elsewhere
1,4,38,39
.
Using the subscript to highlight that the following vectors are expressed in laboratory
coordinates
30
, we express the exit wave vector as:
(8)
where the third expression in eq. (8) is in spherical coordinates and the last in Cartesian coordinates.
The way azimuth
(angle between the projection of
on the xy-plane and the x-axis) and
elevation
(angle between
and the xy-plane) are measured corresponds to the way azimuth
and elevation are measured for the detector (see Figure 1d).
The incident wave vector in laboratory coordinates
30
points towards the
axis:
(9)

5
therefore the scattering vector in laboratory coordinates
30
is:
(10)
The angle between the incident and exit vector is
. It is easy to verify that
Let’s consider a ray described by the product of a scalar (distance) and the exit wave
versor
(direction) pointing towards the unrotated detector and with its origin in the origin of the
laboratory system:
(11)
The length of the ray is controlled by the scalar . If the detector circle angles are zero, the detector’s
normal (versor) is:
(12)
We would like to calculate so that is on the detector plane. The plane can be described by the
scalar product
31-34
:
(13)
where is a point on the plane, and is the distance between the plane and the origin of the
laboratory coordinates. Substituting eq. (11) in eq. (13) we get:
(14)
When the detector is at non-zero circle angles (
,
, and )
rotates according to
(first
column):
(15)
Therefore the ray intersects the detector at:
(16)
If we use Cartesian coordinates for
:

6
(17)
We observe that since
is a versor
, and that therefore it only requires two
elements to be described. With eq. (16) or eq. (17) we can calculate the intersection between a ray
with origin in the origin of the laboratory system and the plane passing by the detector. The
intersecting point is represented in laboratory coordinates.
We will now represent the ray intersecting the detector plane in detector coordinates. The
following calculations can be performed in MATLAB with Script 4, Supplementary Information. The
image coordinates correspond to the way the image matrix is indexed. Depending on the convention
used, the row index (y-axis) and the column index (x-axis) might correspond to the top left
corner. If the image size is , then and , corresponds to the bottom right corner.
We would like to use a different coordinate system for the detector, having as the centre the pixel hit
by the direct beam (incident wave vector). If the direct beam points towards the centre of the
detector, we chose the centre of the detector reference system as
and
. This
corresponds to defining the following image coordinates as:
(18)
When the detector circle angles are zero, its origin expressed in laboratory coordinates is:
(19)
and its basis is:
(20)
When the detector circle angles
,
, are non-zero, the detector basis rotates according to:
(21)
Therefore a ray intersecting the detector at a point has the following coordinates in the detector
reference system:
(22)

7
which can also be rewritten as
. Eq. (22) can be rewritten by using the expression
for (eq. (16)) and the expression for
and
(eq. (21)) in spherical coordinates
(23)
and in Cartesian coordinates:
(24)
The following calculations can be performed in MATLAB with Script 6, Supplementary Information.

8
Case 1. The detector is at its origin (
):
(25)
Case 2. If we substitute
in eq. (25)
(26)
and
and
.
Case 3. With , if
(
, ),
, the projection of
is at the origin of the detector (see Example 3 case 3 in the
software).
Rotating the Sample Circles
We now consider the last reference system, the sample coordinates system , which is represented
by the versors
(see Figure 1d). Following You’s
30
formalism we indicate the crystal
momentum transfer in the reciprocal space coordinates as:
(27)
where
are the reciprocal lattice vectors:
1,4,38,39
If the basis of the reciprocal space is different
from the laboratory basis, we can then construct a matrix so that the momentum transfer is
expressed in the laboratory basis:
30
(28)
The crystal might have some intrinsic preferential orientation with respect to the sample substrate.
This is represented by a rotation matrix (orientation matrix) so that
30
:
(29)
The momentum transfer
gives information about the crystal and its orientation. The diffraction
condition is
30
:
(30)
where we have used the subscript to indicate that the vector
are expressed in the sample
reference system.
Now we would like to see what happens to these vectors when the sample circle is rotated. We
would like to calculate the effect of a sample rotation on the ray projected on the detector plane.
9
When all the sample circles are zero, the sample basis corresponds to the laboratory basis
. The rotation of any of the sample circles reorients the sample basis and the sample or
crystal itself, according to a rotation matrix given by the composition of these rotations. In case of
sample rotating circles mounted one on each other, the way to build the total rotation matrix proceeds
from the inner circle to the outer circle as
. Here we only consider the
case in which the pitch (
) is rotated. Therefore, we will just use one rotation matrix
. As mentioned
above, a positive pitch rotation corresponds to a clockwise rotation of the sample with respect to
(see Figure 1d), and the rotation matrix is:
(31)
A pitch rotation, changes the sample basis from where all the sample circles are zero, to:
(32)
In this simple case, the total rotation matrix is simply
. In the presence of such a rotation the
momentum transfer rotates according to
30
:
(33)
The diffraction condition is
30
:
(34)
The matrix
rotates the wave vectors
and
counterclockwise about
, and allows to
express them as
and
in sample coordinates
. Therefore the incident wave vectors in
the laboratory and sample reference system are (see ref.
30
equation (12), where
is our
):
(35)

10
The exit wave vectors in the laboratory and sample basis are:
(36)
where
and
are the azimuth and the elevation of
in spherical coordinates:
(37)
The rotated scattering vector in the laboratory and sample reference system are:
(38)
If we convert the detector coordinates from pixels to
we will be able to observe the reflection
at the same point on the detector as
varies. This is the most important concept of this paragraph.
If we exclude refraction effects
40
, by employing
as the image coordinates we can remove distortion
effects in the diffraction pattern introduced by a non-zero pitch. Note that eq.
is equivalent to the
relations mapping the image of the untilted fibre from the detector plane into reciprocal space, which
is reported in ref.
41
.
Finally, the reciprocal space mapping conversion procedure can be summarized as follows:
1. Define pixel reference system for the diffraction image. There might be cases in which,
when the detector and sample circle angles are zero, the direct beam is not at the centre of
the detector. In this case the origin of the image
cannot be at the centre of the
diffraction pattern, and has to be set to the point where the direct beam hits the detector (eq.
(18));
2. Extract image pixel coordinates from the diffraction image and retrieve
,
, and
. If the detector is mounted on the detector circles the distance can be calculated by
tracking the direct beam, as shown in ref.
40
. The angles
,
, are immediately available
if the detector is mounted on the detector circles. However there can be cases in which the
detector is mounted elsewhere (e.g. linear stages). In this case a calibration material (e.g. silver
behenate) can be used for the extraction of
,
, and .
3. Use eq. (24) to convert to
;
4. Use eq. (36) to obtain
from
;
5. Use eq. (38) to calculate the momentum transfer or scattering vector
in the sample
reference system;

11
6. Remap the intensities (interpolation) from the original diffraction image in coordinates
into suitable 2D coordinates for
, for example
as the ordinate and
as the abscissa.
Conclusion
In this work we have derived, in a rigorous way, the reciprocal space mapping equations for a ‘3D+1S’
diffractometer in a way that is understandable to anyone with basic notions of linear algebra,
geometry, and X-ray diffraction. With this set of equations, starting from the detector and sample
circle angles and the distance sample-detector one can convert a diffraction image represented in
pixel coordinates to the momentum transfer or scattering vector in the sample reference system.
References
1 Birkholz, M. Thin film analysis by X-ray scattering. (John Wiley & Sons, 2006).
2 Vlieg, E., Van der Veen, J., Macdonald, J. & Miller, M. Angle calculations for a five-circle
diffractometer used for surface X-ray diffraction. Journal of applied crystallography 20, 330-
337, (1987).
3 Feidenhans, R. Surface structure determination by X-ray diffraction. Surface Science Reports
10, 105-188, (1989).
4 Als-Nielsen, J. & McMorrow, D. Elements of modern X-ray physics. (John Wiley & Sons, 2011).
5 Ungar, G., Liu, F., Zeng, X., Glettner, B., Prehm, M., Kieffer, R. et al. in Journal of Physics:
Conference Series. 012032 (IOP Publishing).
6 Grelet, E., Dardel, S., Bock, H., Goldmann, M., Lacaze, E. & Nallet, F. Morphology of open films
of discotic hexagonal columnar liquid crystals as probed by grazing incidence X-ray diffraction.
The European Physical Journal E 31, 343-349, (2010).
7 Perlich, J., Schwartzkopf, M., Körstgens, V., Erb, D., Risch, J., Müller‐Buschbaum, P. et al.
Pattern formation of colloidal suspensions by dip‐coating: An in situ grazing incidence X‐ray
scattering study. Physica status solidi (RRL)-Rapid Research Letters 6, 253-255, (2012).
8 Renaud, G., Lazzari, R. & Leroy, F. Probing surface and interface morphology with Grazing
Incidence Small Angle X-Ray Scattering. Surface Science Reports 64, 255-380, (2009).
9 Bikondoa, O., Carbone, D., Chamard, V. & Metzger, T. H. Ageing dynamics of ion bombardment
induced self-organization processes. Scientific Reports 3, 1850, (2013).
10 Joshi, G. R., Cooper, K., Lapinski, J., Engelberg, D. L., Bikondoa, O., Dowsett, M. G. et al. (NACE
International).
11 Springell, R., Rennie, S., Costelle, L., Darnbrough, J., Stitt, C., Cocklin, E. et al. Water corrosion
of spent nuclear fuel: radiolysis driven dissolution at the UO2/water interface. Faraday
Discussions 180, 301-311, (2015).
12 Katsouras, I., Asadi, K., Li, M., van Driel, T. B., Kjaer, K. S., Zhao, D. et al. The negative
piezoelectric effect of the ferroelectric polymer poly(vinylidene fluoride). Nat Mater, (2015).
13 Müller-Buschbaum, P. Grazing incidence small-angle X-ray scattering: an advanced scattering
technique for the investigation of nanostructured polymer films. Anal Bioanal Chem 376, 3-
10, (2003).
14 Dane, T. G., Cresswell, P. T., Pilkington, G. A., Lilliu, S., Macdonald, J. E., Prescott, S. W. et al.
Oligo(aniline) nanofilms: from molecular architecture to microstructure. Soft Matter 9, 10501-
10511, (2013).
15 Al-Jawad, M., Steuwer, A., Kilcoyne, S. H., Shore, R. C., Cywinski, R. & Wood, D. J. 2D mapping
of texture and lattice parameters of dental enamel. Biomaterials 28, 2908-2914, (2007).
16 Simmons, L. M., Al‐Jawad, M., Kilcoyne, S. H. & Wood, D. J. Distribution of enamel crystallite
orientation through an entire tooth crown studied using synchrotron X‐ray diffraction.
European journal of oral sciences 119, 19-24, (2011).

12
17 Beddoes, C. M., Case, C. P. & Briscoe, W. H. Understanding nanoparticle cellular entry: A
physicochemical perspective. Advances in Colloid and Interface Science 218, 48-68, (2015).
18 Renaud, G. Oxide surfaces and metal/oxide interfaces studied by grazing incidence X-ray
scattering. Surface Science Reports 32, 5-90, (1998).
19 Staniec, P. A., Parnell, A. J., Dunbar, A. D., Yi, H., Pearson, A. J., Wang, T. et al. The nanoscale
morphology of a PCDTBT: PCBM photovoltaic blend. Advanced Energy Materials 1, 499-504,
(2011).
20 Agostinelli, T., Ferenczi, T. A., Pires, E., Foster, S., Maurano, A., Müller, C. et al. The role of
alkane dithiols in controlling polymer crystallization in small band gap polymer: Fullerene solar
cells. Journal of Polymer Science Part B: Polymer Physics 49, 717-724, (2011).
21 Lilliu, S., Agostinelli, T., Hampton, M., Pires, E., Nelson, J. & Macdonald, J. E. The Influence of
Substrate and Top Electrode on the Crystallization Dynamics of P3HT: PCBM Blends. Energy
Procedia 31, 60-68, (2012).
22 Lilliu, S., Alsari, M., Bikondoa, O., Macdonald, J. E. & Dahlem, M. S. Absence of Structural
Impact of Noble Nanoparticles on P3HT:PCBM Blends for Plasmon-Enhanced Bulk-
Heterojunction Organic Solar Cells Probed by Synchrotron GI-XRD. Scientific Reports, (2015).
23 Juraić, K., Gracin, D., Šantić, B., Meljanac, D., Zorić, N., Gajović, A. et al. GISAXS and GIWAXS
analysis of amorphous–nanocrystalline silicon thin films. Nuclear Instruments and Methods in
Physics Research Section B: Beam Interactions with Materials and Atoms 268, 259-262, (2010).
24 Treat, N. D., Brady, M. A., Smith, G., Toney, M. F., Kramer, E. J., Hawker, C. J. et al.
Interdiffusion of PCBM and P3HT reveals miscibility in a photovoltaically active blend.
Advanced Energy Materials 1, 82-89, (2011).
25 Rogers, J. T., Schmidt, K., Toney, M. F., Kramer, E. J. & Bazan, G. C. Structural order in bulk
heterojunction films prepared with solvent additives. Advanced Materials 23, 2284-2288,
(2011).
26 Büchele, P., Richter, M., Tedde, S. F., Matt, G. J., Ankah, G. N., Fischer, R. et al. X-ray imaging
with scintillator-sensitized hybrid organic photodetectors. Nature Photonics, (2015).
27 Tsao, H. N., Cho, D., Andreasen, J. W., Rouhanipour, A., Breiby, D. W., Pisula, W. et al. The
Influence of Morphology on High‐Performance Polymer Field‐Effect Transistors. Advanced
Materials 21, 209-212, (2009).
28 Nelson, T. L., Young, T. M., Liu, J., Mishra, S. P., Belot, J. A., Balliet, C. L. et al. Transistor paint:
high mobilities in small bandgap polymer semiconductor based on the strong acceptor,
diketopyrrolopyrrole and strong donor, dithienopyrrole. Advanced Materials 22, 4617-4621,
(2010).
29 He, B. B. Two-dimensional X-ray diffraction. (John Wiley & Sons, 2011).
30 You, H. Angle calculations for a `4S+2D' six-circle diffractometer. Journal of Applied
Crystallography 32, 614-623, (1999).
31 Banchoff, T. & Wermer, J. Linear algebra through geometry. (Springer Science & Business
Media, 2012).
32 Bloom, D. M. Linear algebra and geometry. (CUP Archive, 1979).
33 Kostrikin, A. I., Manin, Y. I. & Alferieff, M. E. Linear algebra and geometry. (Gordon and Breach
Science Publishers, 1997).
34 Shafarevich, I. R. & Remizov, A. Linear algebra and geometry. (Springer Science & Business
Media, 2012).
35 Hase, T. Beamline Description,
<http://www2.warwick.ac.uk/fac/cross_fac/xmas/description/> (2015).
36 Boesecke, P. Reduction of two-dimensional small-and wide-angle X-ray scattering data.
Applied Crystallography, (2007).
37 Murray, G. Rotation About an Arbitrary Axis in 3 Dimensions,
<http://inside.mines.edu/fs_home/gmurray/ArbitraryAxisRotation/> (2013).

13
38 Woolfson, M. M. An introduction to X-ray crystallography. (Cambridge University Press,
1997).
39 Warren, B. E. X-ray Diffraction. (Courier Corporation, 1969).
40 Lilliu, S., Agostinelli, T., Pires, E., Hampton, M., Nelson, J. & Macdonald, J. E. Dynamics of
crystallization and disorder during annealing of P3HT/PCBM bulk heterojunctions.
Macromolecules 44, 2725-2734, (2011).
41 Stribeck, N. & Nöchel, U. Direct mapping of fiber diffraction patterns into reciprocal space.
Journal of Applied Crystallography 42, 295-301, (2009).
42 Ohad, G. fit_ellipse, <http://www.mathworks.com/matlabcentral/fileexchange/3215-fit-
ellipse> (2003).

14
Supplementary Information
Symbolic Calculations
The following scripts are independent from the detector-GUI Matlab software and require the
Symbolic Math Toolbox.
Script 1 – Arbitrary matrix rotation constructor. This function is used in the following scripts.
function R = arb_rot_sim(a,vect)
% Rotation about arbitrary axis for symb calculations
%vect = vect / norm (vect);
u = vect(1); v = vect(2); w = vect(3);
u2 = u^2 ; v2 = v^2 ; w2 = w^2;
c = cos(a); s = sin(a);
R(1,1) = u2 + (1-u2)*c;
R(1,2) = u*v*(1-c) - w*s;
R(1,3) = u*w*(1-c) + v*s;
R(2,1) = u*v*(1-c) + w*s;
R(2,2) = v2 + (1-v2)*c;
R(2,3) = v*w*(1-c) - u*s;
R(3,1) = u*w*(1-c) - v*s;
R(3,2) = v*w*(1-c)+u*s;
R(3,3) = w2 + (1-w2)*c;
Script 2 – Calculates rotation matrices. See Tracking the Detector Movement.
%% Tracking the Detector Movement
clear all
syms h2 v2 om real % detector rotation angles (azimuth, elevation, omega)
Rx = arb_rot_sim(om,[1 0 0]') % eq.(2)
Ry = arb_rot_sim(v2,-[0 1 0]') % eq.(3)
Rz = arb_rot_sim(h2,[0 0 1]') % eq.(4)
Rxyz = simplify(Rz*Ry*Rx) % eq.(5), total rot. matrix
isequal(simplify(Rxyz'), simplify(Rxyz^-1)) % matrix orthogonality check
isequal(simplify(det(Rxyz)),1) % det = 1 check
Ryz = simplify(Rz*Ry) % eq.(7), total rot. matrix with om = 0
Script 3 – Projecting a ray onto the detector. Running Script 2 is required before running this script. See
Projecting the Exit Wave Vector onto the Detector.
%% Projecting a Ray onto the Detector
syms H2 V2 d real % ray azimuth and elevation, sample-dectector distance
syms vx vy vz real % ray Cartesian coordiantes
n = [1 0 0]' % eq.(9), normal versor to unrotated detector
[V(1) V(2) V(3)] = sph2cart(H2, V2, 1); V = V' % eq.(12), ray sph. coord
n2 = Rxyz*n % eq.(13), rotated versor
P = d*V/dot(V, n2) % eq.(14), intersection point with detector
Pnum = d*V % numerator in eq. (14)
Pden = dot(V, n2) % numerator in eq. (14)
Vxyz = [vx vy vz]' % eq.(15), ray Carthesian coordinates
P1 = d*Vxyz/dot(Vxyz, n2) % eq.(15), intersection point with detector
P1num = d*Vxyz % numerator in eq. (15)
P1den = dot(Vxyz, n2) % numerator in eq. (15)
Script 4 – Projecting a ray onto the detector. Running Script 3 is required before running this script.
%% Ray Projection on Detector Coordinate System
dy = [0 1 0 ]' % detector x axis
dz = [0 0 1 ]' % detector y axis
dx = [0 0 0 ]' % zero column, detector coord are in 2D
D = [dx , dy, dz] % eq.(18) detector basis
dy2 = Rxyz*dy % eq.(19) roatated detector x axis

15
dz2 = Rxyz*dz % eq.(19) rotated detector y axis
D2 = Rxyz*D % eq.(19) rotated detector coordinate system
x = simplify(dot(P, dy2)); % eq.(21), point P in detector coordiantes
y = simplify(dot(P, dz2)); % eq.(21), point P in detector coordiantes
x1 = simplify(dot(P1, dy2)); % eq.(22), point P in detector coordiantes
y1 = simplify(dot(P1, dz2)); % eq.(22), point P in detector coordiantes
x1 = simplify(subs(x1, vz, sqrt(1-vx^2-vy^2))) % eq.(22)
y1 = simplify(subs(y1, vz, sqrt(1-vx^2-vy^2))) % eq.(22)
simplify(subs(x1, om, 0)) % eq.(24)
simplify(subs(y1, om, 0)) % eq.(24)
Script 5 – Projecting a ray onto the detector. Running Script 4 is required before running this script. See Error!
Reference source not found..
%% Finding a Ray from a Point on the Detector
syms X Y real
[vx_s vy_s] = solve([X == x1, Y == y1], vx, vy) % inverting eq.(22)
simplify(vx_s(2)) % eq.(25), vx (only the second solution makes sense)
simplify(vy_s(2)) % eq.(25), vy
vz_s = simplify(sqrt(1-vx_s(2)^2-vy_s(2)^2))
subs(simplify(vx_s(2)), om, 0) % eq.26, vx
subs(simplify(vy_s(2)), om, 0) % eq.26, vy
Script 6 – Example 2. Running script 5 is required before running this script. See Error! Reference source not
found..
%% Example 2
% case 1
subs(vx_s(2), [h2 v2 om], [0 0 0]) % eq.(40), vx
subs(vy_s(2), [h2 v2 om], [0 0 0]) % eq.(40), vy
simplify(subs(vz_s, [h2 v2 om], [0 0 0])) % eq.(4), vz
% case 3
c3x = double(subs(vx_s(2), [h2 v2 X Y d om], [pi/6 pi/6 0 0 1 0])) % eq.(43)
c3y = double(subs(vy_s(2), [h2 v2 X Y d om], [pi/6 pi/6 0 0 1 0])) % eq.(43)
c3z = double(simplify(subs(vz_s, [h2 v2 X Y d om], [pi/6 pi/6 0 0 1 0])))%
eq.(43)
c3 = [c3x c3y c3z];
[ca ce cr] = cart2sph(c3x, c3y, c3z);
ca_deg = rad2deg(ca) % eq.(44)
ce_deg = rad2deg(ce) % eq.(44)
Script 7 – Scattering Vector.
%% Defining the Ray as the Scattering Vector
syms lam real % wave vector amplitude 2pi/lambda
k = 2*pi/lam;
ki = [1 0 0]'
kf = V
q = kf-ki % eq.(35)
simplify(acos(dot(ki, kf))) % Bragg angle
simplify(sqrt(dot(q,q))) % eq. (37) norm of q0
syms a b c real
a1 = [a 0 0]
a2 = [0 b 0]
a3 = [0 0 c]
b1 = 2*pi*(cross(a2, a3)/dot(a1,(cross(a2, a3))))
b2 = 2*pi*(cross(a3, a1)/dot(a2,(cross(a3, a1))))
b3 = 2*pi*(cross(a1, a2)/dot(a3,(cross(a1, a2))))

16
Script 8 – Unrotated exit wave vector. Running script 6 is required before running this script.
%% Rotating the sample circles
syms ai real
kfx = simplify(vx_s(2)) % eq.25, vx
kfy = simplify(vy_s(2)) % eq.25, vy
kfz = simplify(sqrt(1-vx_s(2)^2-vy_s(2)^2))
kf = [kfx; kfy; kfz]
Ai = arb_rot_sim(ai,-[0 1 0]'); % eq.(45) pitch rotation matrix
