Name:
Math 230
Mock Final Exam Detailed Solution
Disclaimer: This mock exam is for practice purposes only. No graphing calulators ≥ TI-89 is allowed on
this test. Be sure that all of your work is shown and that it is well organized and legible.
Warning: Some of the problems can be done different ways. I do not show them all.
This mock exam does not cover all the material that can be tested on the final. Please review all your
exams, quizzes, and homeworks.
Good luck!
Calculus Tutoring Center
DU 326
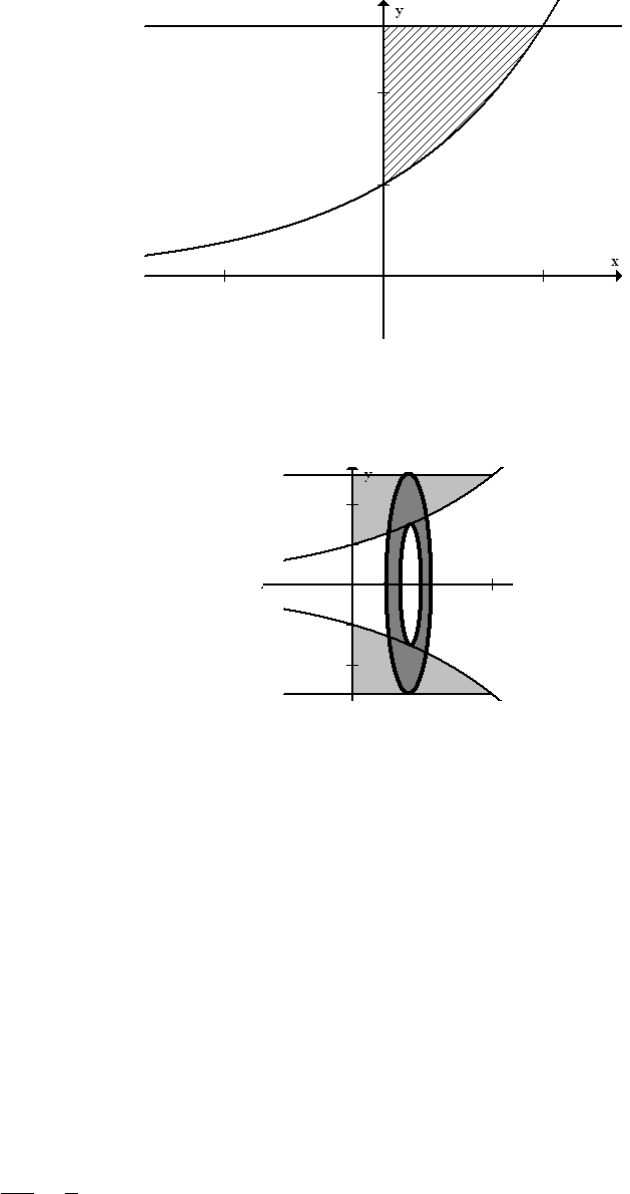
1. (16 points)
(a) Sketch the region bounded by y = e
x
, y = e, and x = 0.
(b) Set up, but do not evaluate, an integral which determines the volume of the solid generated by
revolving the region in (a) about the x-axis.
i. Formula for the Washer Method:
Z
b
a
π(R(x))
2
− π(r(x))
2
dx
ii. Find R(x):
R(x) = e
iii. Find r(x):
r(x) = e
x
iv. Bounds:
a = 0, b = 1
v. Use Formula:
Volume =
Z
1
0
π(e)
2
− π(e
x
)
2
dx
Volume = π
Z
1
0
e
2
− e
2
x dx
vi. Evaluating this integral isn’t too difficult. You should try doing it as practice. The integral
is
πe
2
2
+
π
2
(c) Set up, but do not evaluate, an integral which determines the volume of the solid generated by
revolving the region in (a) about the y-axis.
Using the Shell Method:

i. Formula for Shell Method:
Z
b
a
2π (radius) ·(height)
ii. Find Radius:
Radius = x
iii. Find Height:
Height = e −e
x
iv. Bounds:
a = 0, b = 1
v. Use the Formula:
Volume =
Z
1
0
2π(x)(e − e
x
) dx
vi. If you evaluate it, you should get V = π(e − 2)
Using the Washer Method:
i. Formula for Washer Method:
Z
d
c
π(R(y))
2
− π(r(y))
2
dx
ii. Find R(y):
R(y) = ln y
iii. Find r(y).
Since there is no inner radius, r(y) = 0.
iv. Bounds:
c = 1, d = e

v. Use the Formula:
Volume =
Z
e
1
π(R(y))
2
dy
Volume =
Z
e
1
π(ln y)
2
dy
vi. If you evaluate it, you should get V = π(e − 2)
2. (16 points) Compute the derivatives of the following functions. Do not simplify your answer.
(a) f(x) = tan
−1
(1 − 2
x
)
f
0
(x) =
1
1 + (1 − 2
x
)
2
· (−2
x
· ln 2) =
−2
x
ln 2
1 + (1 − 2
x
)
2
(b) f(x) = (x
2
+ 2)
x
i. We will use logarithmic differentiation
ii. Rewrite the function as y = (x
2
+ 2)
x
iii. Take ln of both sides
ln y = x ln(x
2
+ 2)
iv. Differentiation both sides
1
y
· y
0
= x ·
1
x
2
+ 2
· 2x + ln(x
2
+ 2)
y
0
= y
2x
2
x
2
+ 2
+ ln(x
2
+ 2)
y
0
= (x
2
+ 2)
x
2x
2
x
2
+ 2
+ ln(x
2
+ 2)
3. (10 points) Find the length of the curve y =
x
2
8
− ln x from x = 1 to x = 4.
Formula for Arc Length:
Z
b
a
p
1 + (y
0
)
2
dx
(a) Write out y:
y =
x
2
8
− ln(x)
(b) Find y
0
y
0
=
x
4
−
1
x
y
0
=
x
2
− 4
4x

(c) Find 1 + (y
0
)
2
1 +
x
2
− 4
4x
2
= 1 +
(x
2
− 4)
2
16x
2
=
16x
2
+ (x
2
− 4)
2
16x
2
=
16x
2
+ x
4
− 8x
2
+ 16
16x
2
=
x
4
+ 8x
2
+ 16
16x
2
=
(x + 4)
2
16x
2
(d) Use formula:
Z
4
1
p
1 + (y
0
)
2
dx
=
Z
4
1
r
(x + 4)
2
16x
2
dx
=
Z
4
1
x
2
+ 4
4x
dx
=
Z
4
1
x
2
4x
+
4
4x
dx
=
Z
4
1
x
4
+
1
x
dx
=
x
2
8
+ ln(x)
4
1
15
8
+ ln(4)
4. (12 points) Let f(x) = 2e
3x
+ x
(a) Use f
0
(x) to explain why f
−1
(x) exists on (−∞, ∞).
Solution: If a function is always increasing or always decreasing, then it is 1-1. When a func-
tion is 1-1, it has an inverse function f
−1
(x). So let’s see if f(x) is always increasing or always
decreasing.
f
0
(x) = 6e
3x
+ 1
and
f
0
(x) = 6e
3x
+ 1 > 0
for all x. Therefore, f(x) is always increasing and we can conclude is 1-1.
Since it’s 1-1, f
−1
(x) exists for all x.

(b) Find
f
−1
0
(2). Note: f (0) = 2.
We have a formula for this:
(f
−1
)
0
(2) =
1
f
0
(f
−1
(2))
i. Find f
−1
(2).
By definition, f
−1
(2) = b if f(b) = 2. We are given that f(0) = 2. Therefore, f
−1
(2) = 0.
ii. Find f
0
(x)
f
0
(x) = 6e
3x
+ 1
iii. Evaluate f
0
(f
−1
(2))
f
0
(0) = 6e
0
+ 1 = 7
iv. Plug it back into the formula
(f
−1
)
0
(2) =
1
f
0
(f
−1
(2))
=
1
7
5. (16 points) Compute the following limits
(a) lim
x→0
x
2
1 − cos(2x)
lim
x→0
x
2
1 − cos(2x)
LH0/0
→ lim
x→0
2x
2 sin(2x)
LH0/0
→ lim
x→0
2
4 cos(4x)
=
1
2
(b) lim
n→∞
1 −
1
2n
3n
This problem has two approaches. My approach for this problem will be to rewrite
1 −
1
2n
3n
as
1 −
1
2n
3n
= e
3n ln
(
1−
1
2n
)

This limit will exist as long as lim
n→∞
3n ln
1 −
1
2n
exists.
lim
n→∞
3n ln
1 −
1
2n
= lim
n→∞
ln
1 −
1
2n
1
3n
LH0/0
→ lim
n→∞
1
1−
1
2n
·
1
2n
2
−
1
3n
2
= lim
n→∞
1
1−
1
2n
·
1
2
1
3
= −
3
2
Therefore,
lim
n→∞
1 −
1
2n
3n
= e
−3/2
6. (50 points) Evaluate the following integrals:
(a)
Z
3x − 5
x
2
− 4x + 3
dx
i. We will do this problem by using partial fractions.
3x − 5
x
2
− 4x + 3
=
A
x − 1
+
B
x − 3
ii. We need to find A and B
iii. Multiply both sides by the common denominator (x − 1)(x − 3)
3x − 5 = A(x − 3) + B(x − 1)
iv. Plug in x = 3, we get
4 = 2B → B = 2
v. Plug in x = 1, we get
−2 = −2A → A = 1
vi. Rewrite the integral and evaluate
Z
3x − 5
x
2
− 4x + 3
dx =
Z
1
x − 1
+
2
x − 3
dx
= ln |x − 1| + 2 ln |x − 3| + C

(b)
Z
sec
4
(x) dx
i. Since the integrand is a power of a trig function, we’ll try the method from the Trig Integral
section. Note that the power of sec(x) is even.
ii. Pull out a factor of sec
2
(x)
Z
sec
2
(x) · sec
2
(x) dx
iii. Rewrite the rest of the sec
2
(x)s as 1 + tan
2
(x).
Z
(1 + tan
2
(x)) sec
2
(x) dx
iv. Let u = tan(x) and du = sec
2
(x) dx
v. Now substitute
Z
(1 + tan
2
(x)) sec
2
(x) dx =
Z
(1 + u
2
) du
vi. Evaluate the integral
Z
(1 + u
2
) du = u +
1
3
u
3
+ C
vii. Replace u with tan(x)
Z
sec
4
(x) dx = tan(x) +
1
3
tan
3
(x) + C
(c)
Z
x
2
√
4 − x
2
dx
i. This method requires trig substitution.
ii. Let x = 2 sin(θ) and dx = 2 cos(θ) dθ
Z
x
2
√
4 − x
2
dx =
Z
4 sin
2
(θ)
p
4 − 4 sin
2
(θ)
2 cos(θ) dθ
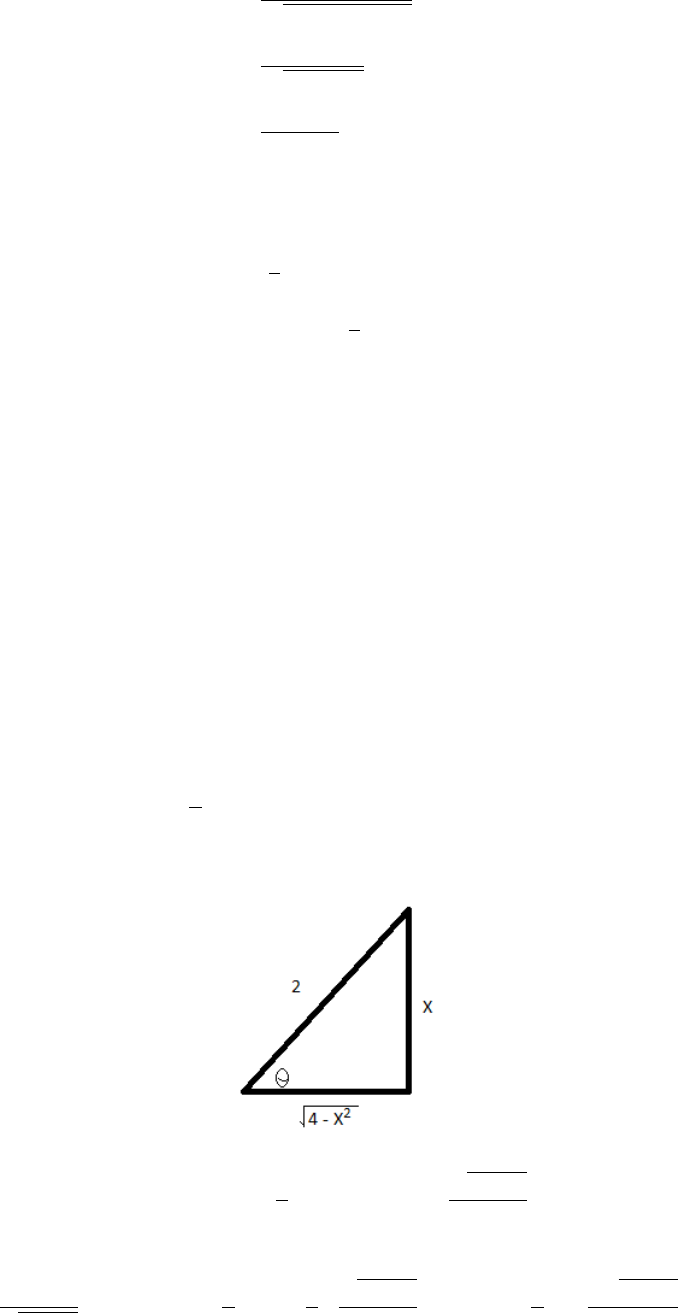
iii. Simplify the integrand
=
Z
4 sin
2
(θ)
p
4(1 − sin
2
(θ))
2 cos(θ) dθ
=
Z
4 sin
2
(θ)
p
4 cos
2
(θ)
2 cos(θ) dθ
=
Z
4 sin
2
(θ)
2 cos(θ)
2 cos(θ) dθ
=
Z
4 sin
2
(θ) dθ
iv. We need the trig identity: sin
2
(θ) =
1
2
(1 − cos(2θ))
4 sin
2
(θ) = 4 ·
1
2
(1 − cos(2θ))
= 2(1 − cos(2θ))
= 2 − 2 cos(2θ)
v. Resume the integral
Z
4 sin
2
(θ) dθ =
Z
2 − 2 cos(2θ) dθ
= 2θ − sin(2θ) + C
vi. We need the trig identity sin(2θ) = 2 sin(θ) cos(θ)
Z
4 sin
2
(θ) dθ = 2θ − 2 sin(θ) cos(θ) + C
vii. Use x = 2 sin(θ) → sin(θ) =
x
2
and the following triangle to get back to a function in terms
of x.
θ = sin
−1
x
2
and cos(θ) =
√
4 − x
2
2
viii. Final Answer
Z
x
2
√
4 − x
2
dx = 2 sin
−1
x
2
− 2 ·
x
2
·
√
4 − x
2
2
= 2 sin
−1
x
2
−
x
√
4 − x
2
2
+ C
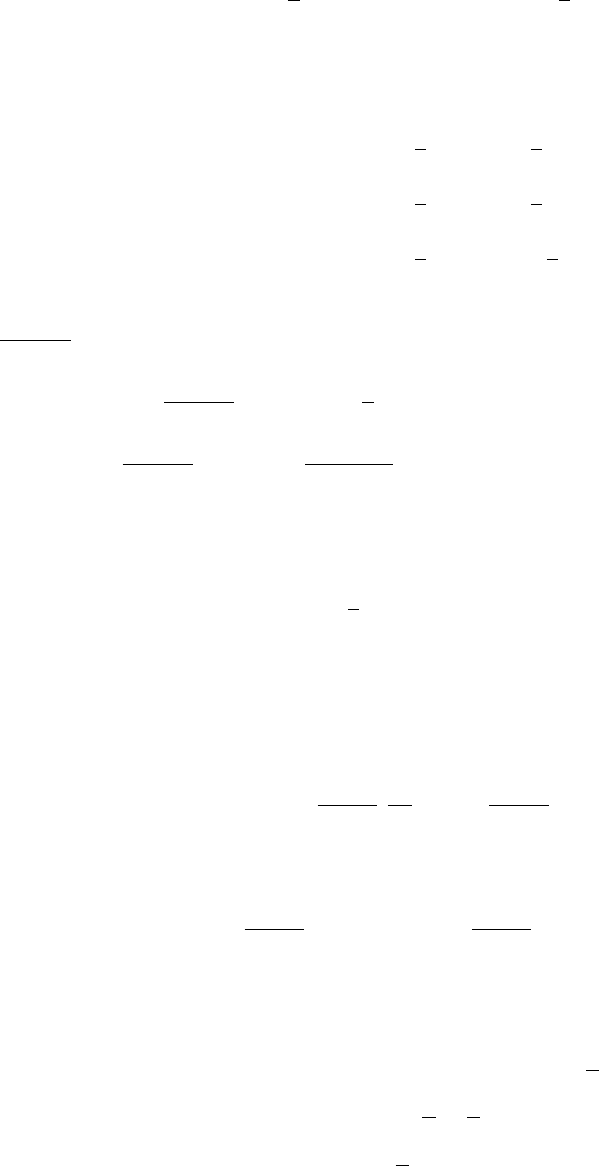
(d)
Z
x
2
ln x dx
i. Let’s try integration by parts.
ii. Let u = ln(x) and dv = x
2
dx
u = ln(x) dv = x
2
dx
du =
1
x
dx v =
1
3
x
3
iii. Formula for integration by parts:
R
u dv = uv −
R
v du
Z
x
2
ln(x) dx =
1
3
x
3
ln(x) −
1
3
Z
x
2
dx
=
1
3
x
3
ln(x) −
1
9
x
3
+ C
=
1
3
x
3
ln(x) −
1
3
+ C
(e)
Z
∞
1/2
4
1 + 4x
2
dx
i. This looks like
Z
1
a
2
+ x
2
dx, which is
1
a
tan
−1
(x/a). But we need to do a substitution first.
ii. Rewrite
Z
∞
1/2
4
1 + 4x
2
dx as
Z
∞
1/2
4
1 + (2x)
2
dx
iii. Let u = 2x and du = 2 dx
iv. We need to change the bounds:
If x =
1
2
, then u = 2(1/2) = 1
If x = ∞, then u = 2(∞) = ∞
v. Substitute everything in and we get
Z
∞
1
4
1 + u
2
du
2
=
Z
∞
1
2
1 + u
2
du
vi. Evaluate the integral. Note this is an improper integral!
Z
∞
1
2
1 + u
2
du = lim
t→∞
Z
t
1
2
1 + u
2
du
= lim
t→∞
2 tan
−1
(u)
t
1
= lim
t→∞
2 tan
−1
(t) − 2 tan
−1
(1)
= 2 lim
t→∞
tan
−1
(t) − 2 ·
π
4
= 2 ·
π
2
−
π
2
=
π
2

7. (10 points) Find the sum of the series
∞
X
n=1
1
2
n
+
(−1)
n
3
n
(a) Split the series into two separate series
∞
X
n=1
1
2
n
+
(−1)
n
3
n
=
∞
X
n=1
1
2
n
+
∞
X
n=1
(−1)
n
3
n
(b) Rewrite as a geometric series
∞
X
n=1
1
2
n
+
∞
X
n=1
(−1)
n
3
n
=
∞
X
n=1
1
2
n
+
∞
X
n=1
−1
3
n
(c) Warning!! The formula for a geometric series is
∞
X
n=1
ar
n−1
=
a
1 − r
or
X
n=0
ar
n
=
a
1 − r
(d) Since the index is n = 1, the exponent needs to be r
n−1
.
X
n=1
1
2
n
=
∞
X
n=1
1
2
1
2
n−1
=
1/2
1 − 1/2
= 1
X
n=1
−1
3
n
=
∞
X
n=1
−1
3
·
−1
3
n−1
=
−1/3
1 − (−1/3)
= −
1
4
(e) Finish the problem
∞
X
n=1
1
2
n
+
(−1)
n
3
n
= 1 +
−1
4
=
3
4
8. (16 points) For each of the following series, determine whether it is convergent or divergent. Justify
your answer.
(a)
X
n=2
1
(n + 1) ln(n + 1)
i. We’ll use the integral test.
ii. Recall that if the series satisfies the condtions for the integral test and the integral
Z
∞
2
1
(x + 1) ln(x + 1)
dx
converges, then so does the series.
iii. Let u = ln(x + 1) and du =
1
x + 1
dx
iv. Change the bounds:
If x = 2, u = ln(3)
If x = ∞, u = ln(∞ + 1) = ∞

v. Substitute everything and evaluate
Z
∞
2
1
(x + 1) ln(x + 1)
dx =
Z
∞
ln 3
1
u
du
= lim
t→∞
Z
t
ln 3
1
u
du
= lim
t→∞
ln(u)|
t
ln 3
= lim
t→∞
ln t − ln(ln 3)
= ∞
vi. Since the integral diverges, by the Integral Test the series
X
n=2
1
(n + 1) ln(n + 1)
also diverges.
(b)
X
1
n + 2
n
i. Let’s try a comparison test. Since I see 2
n
on the denominator and it’s the dominant term
in the sequence, I anticipate the series converges. With a direct comparison test, my job is
to find a larger series that converges.
ii. Since n + 2
n
> 2
n
for n ≥ 1, we have
1
n + 2
n
≤
1
2
n
iii. This means we have the following direct comparison
X
1
n + 2
n
≤
X
1
2
n
=
X
1
2
n
iv. Since
X
1
2
n
is geometric and converges (−1 <
1
2
< 1), it forces our smaller series
X
1
n + 2
n
to converge as well.
9. (12 points) Determine whether each of the following series is absolutely convergent, conditionally
convergent, or divergent. Justify your answer.
(a)
∞
X
n=1
(−1)
n+1
sin(n)
n(n + 1)
i. If you can show
X
|a
n
| converges, then
X
a
n
converges absoutely. We usually use this
approach when we have a sin(n) or cos(n) function in our sequence.
ii. Let’s determine the convergence of
X
(−1)
n+1
sin(n)
n(n + 1)

X
(−1)
n+1
sin(n)
n(n + 1)
=
X
|sin(n)|
n(n + 1)
≤
X
1
n(n + 1)
=
X
1
n
2
+ n
≤
X
1
n
2
iii. And
X
1
n
2
converges by p-series (p = 2).
iv. By the Direct Comparison Test, since
X
(−1)
n+1
sin(n)
n(n + 1)
converges,
∞
X
n=1
(−1)
n+1
sin(n)
n(n + 1)
converges absolutely.
(b)
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
i. Let’s go ahead and try the Alternating Series Test. Let b
n
=
n + 1
n
2
ln(n)
b
n
=
n + 1
n
2
ln(n)
> 0 for n ≥ 2
b
n
is decreasing (you can trust me)
lim
n→∞
n + 1
n
2
ln(n)
= 0
Since b
n
satisfies the requirements for the alternating series test, we can say
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
converges
ii. But the question is to determine if it’s absolutely or conditionally convergent. The alternat-
ing series test does not determine this. To check for absolute or conditional, we determine
if
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
converges or diverges
iii. Let’s go ahead and try to simplify and/or compare this to other known series.
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
=
∞
X
n=2
n + 1
n
2
ln(n)
≥
∞
X
n=2
n
n
2
ln(n)
=
∞
X
n=2
1
n ln(n)
which diverges by the integral test

I’ll let you verify this diverges by the integral test.
iv. Since
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
diverges and
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
converges , we conclude
∞
X
n=2
(−1)
n+1
n + 1
n
2
ln(n)
converges conditionally
10. (12 points) Find the radius of convergence and interval of convergence of the series
∞
X
n=1
(−1)
n
n
x − 3
2
n
.
(a) When asked to find the interval and radius of convergence, we start by using the Ratio Test.
(b) You should write out a
n+1
and a
n
so you don’t mess it up on the test.
a
n
=
(−1)
n
(x − 3)
n
n2
n
a
n+1
=
(−1)
n+1
(x − 3)
n+1
(n + 1)2
n+1
(c) Now set up the Ratio Test
L = lim
n→∞
a
n+1
a
n
= lim
n→∞
(−1)
n+1
(x − 3)
n+1
(n + 1)2
n+1
·
n2
n
(−1)
n
(x − 3)
n
= lim
n→∞
(−1)
n+1
(−1)
n
·
2
n
2
n+1
·
n
n + 1
·
(x − 3)
n+1
(x − 3)
n
=
x − 3
2
lim
n→∞
(−1)
n
n + 1
=
x − 3
2
· 1
(d) The Ratio Test says if L < 1, the series converges. Since L =
x − 3
2
, we solve
x − 3
2
< 1
−1 <
x − 3
2
< 1
−2 < x − 3 < 2
1 < x < 5
(e) The radius of convergence is R = 2.

(f) We need to check the endpoints of the interval of convergence since it’s possible the series will
converge at x = 1 or x = 5.
i. x = 5
∞
X
n=1
(−1)
n
n
5 − 3
2
n
∞
X
n=1
(−1)
n
n
1
n
∞
X
n=1
(−1)
n
n
which converges by th AST.
ii. x = 1
∞
X
n=1
(−1)
n
n
1 − 3
2
n
∞
X
n=1
(−1)
n
n
(−1)
n
∞
X
n=1
1
n
which diverges by the p-series (p = 1)
(g) The interval of convergence is (1, 5] with radius R = 2
11. (8 points) Find the Taylor Series centered at a = 0 for
Z
cos(x
2
) dx by using the Taylor Series for
cos(x) at a = 0.
(a) Note: A Taylor Series centered at a = 0 is called a Macluarin Series.
(b) There is a list of Macluarin Series you need to memorize from the textbook. One of them is the
Maclaurin Series for cos(x).
cos(x) =
X
(−1)
n
x
2n
(2n)!
(c) To find cos(x
2
), replace x with x
2
in the above serires.
cos(x
2
) =
X
(−1)
n
(x
2
)
2n
(2n)!
=
X
(−1)
n
x
4n
(2n)!
(d) The original question asks us to integrate cos(x
2
). Integrating the Macluarin Series of cos(x
2
)
will be easy.
Z
cos(x
2
) dx =
Z
X
(−1)
n
x
4n
(2n)!
dx =
X
Z
(−1)
n
x
4n
(2n)!
=
X
(−1)
n
x
4n+1
(2n)!(4n + 1)

12. (10 points)
(a) Determine the third degree Taylor Polynomial P
3
(x) for f(x) = ln(2 + x) at a = −1.
i. First, organize a table to find c
n
f(x) = ln(2 + x) → c
0
=
f(−1)
0!
=
0
0!
= 0
f
0
(x) =
1
2 + x
→ c
1
=
f
0
(−1)
1!
=
1
1!
= 1
f
00
(x) =
−1
(2 + x)
2
→ c
2
=
f
00
(−1)
2!
=
−1
2!
= −
1
2
f
000
(x) =
2
(2 + x)
3
→ c
3
=
f
000
(−1)
3!
=
2
3!
=
1
3
ii. 3-rd degree Taylor Polynomial:
3
X
n=0
c
n
(x + 1)
n
= c
0
+ c
1
(x + 1) + c
2
(x + 1)
2
+ c
3
(x + 1)
3
P
3
(x) = 0 + 1(x + 1) −
1
2
(x + 1)
2
+
1
3
(x + 1)
3
P
3
(x) = 1 + x −
1
2
(x + 1)
2
+
1
3
(x + 1)
3
(b) Is P
0
3
(x) the second degree Taylor Polynomial for f
0
(x) at a = −1? Explain.
i. Let’s take a look at P
0
3
(x)
P
0
3
(x) = 1 − (x + 1) + (x + 1)
2
ii. Let’s look at the Taylor Series for g(x) = f
0
(x) =
1
2 + x
at a = −1
iii. Organize a table to find c
n
g(x) =
1
2 + x
→ c
0
=
g(−1)
0!
=
1
1!
= 1
g
0
(x) =
−1
(2 + x)
2
→ c
1
=
g
0
(−1)
1!
=
−1
1!
= −1
g
00
(x) =
2
(2 + x)
3
→ c
2
=
g
00
(−1)
2!
=
2
2!
= 1
which gives us
f
0
(x) ≈ T
2
(x) = 1 − 1(x + 1) + 1(x + 1)
2
which is exactly P
0
3
(x).
13. (6 points) Is
∞
X
n=1
a
n
is a serires for which
P
a
n
= −2, and s
n
is the n-th partial sum for the series,
determine:
(a) lim
n→∞
a
n
=
Solution: Since we know
X
a
n
= −2, it means the series converges. We have a theorem that
states if a series
X
a
n
converges, then lim
n→∞
a
n
= 0
(b) lim
n→∞
s
n
=
Solution: By definition, if a series converges when
X
a
n
= lim
n→∞
s
n
Since
P
a
n
= −2, we have
lim
n→∞
s
n
= −2
14. (6 points) If
P
c
n
x
n
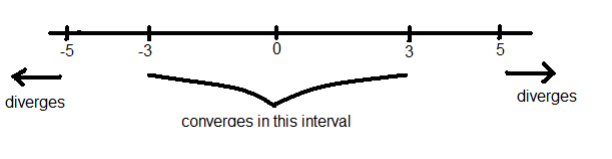
is a convergent power series for x = 3 but not x = 5, can you conlcude that it
converges for (i) x = −2, (ii) x = −3, (iii) x = −6. Explain.
Solution: Based on the information given, we know at least this much about where the series con-
verges. Note, the power series is centered at a = 0.
(a) Since the center is a = 0 and the series converges at x = 3, we know it must converge at least on
the interval (−3, 3). Remember the center a = 0 is the center of the interval of convergence. If
we know it converges 3 units to the right of the center, it must converge up to 3 units to the left.
(b) Does it converge at x = −2?
Yes it does. Worst case scenario, the interval of convergence is (−3, 3]. Since x = −2 is in the
interval, we know it must converge at x = −2.
(c) Does it converge at x = −3?
We cannot conclude anything at x = −3. Remember that we always checked the endpoints of
the interval of convergence. If we wanted to know if it converged at x = −3, we would need to
plug it in and see what happens. Since we don’t know c
n
, we can’t determine convergence.
(d) Does it converge at x = −6?
From the graph, you see that once you go outside the interval (−5, 5), the series is guaranteed to
diverge. If the series can’t converge at x = 5, it can’t converge at any x-value beyond 5. Since
this has to be symmetric about the center, we can also conclude that the series can’t converge
for any x-value less than -5.
No, the series does not converge at x = −6
