
HAL Id: hal-01276223
https://inria.hal.science/hal-01276223
Submitted on 19 Feb 2016
HAL is a multi-disciplinary open access
archive for the deposit and dissemination of sci-
entic research documents, whether they are pub-
lished or not. The documents may come from
teaching and research institutions in France or
abroad, or from public or private research centers.
L’archive ouverte pluridisciplinaire HAL, est
destinée au dépôt et à la diusion de documents
scientiques de niveau recherche, publiés ou non,
émanant des établissements d’enseignement et de
recherche français ou étrangers, des laboratoires
publics ou privés.
Lower bound of the covering radius of binary irreducible
Goppa codes
Sergey Bezzateev, Natalia Shekhunova
To cite this version:
Sergey Bezzateev, Natalia Shekhunova. Lower bound of the covering radius of binary irreducible
Goppa codes. WCC2015 - 9th International Workshop on Coding and Cryptography 2015, Anne
Canteaut, Gaëtan Leurent, Maria Naya-Plasencia, Apr 2015, Paris, France. �hal-01276223�

Lower Bound of the Covering Radius of Binary
Irreducible Goppa Codes
Sergey Bezzateev and Natalia Shekhunova
Saint Petersburg State University of Aerospace Instrumentation, Russia
?
Abstract. The lower bound of the covering radius of binary irreducible
Goppa codes is obtained.
1 Introduction
The covering radius of a linear code C with a length n is defined as the least
integer R(C) such that for any vector x of an n- dimensional space that does not
belong to code C, a codeword c ∈ C is found that is located at a distance not
exceeding R(C). It follows from this definition that the covering radius R(C) of
the binary linear code C can be written as:
R(C) = max {min {w t(x ⊕ c), c ∈ C} , x ∈ Z
n
2
} .
It is known that the problem of finding the covering radius for different classes
of block codes remains topical for a long time because it presents one of the
versions of the classical problem of discrete mathematics: the covering of n -
dimensional vector space with the least number of spheres of radius R(C) in
Hamming metric so that every vector of the space belongs at least to one of the
spheres. The upper and lower bounds of the covering radius for many classes of
block codes were obtained and discussed in papers [1–6].
This paper presents the lower bound of the covering radius of binary irre-
ducible Goppa codes.
Let us consider some definitions that we will use to prove the main result of
this paper.
It is well-known that binary Goppa codes can be defined [7] by a Goppa
polynomial G(x) ∈ IF
2
m
[x], deg G(x) = t and set of numerators of codeword
positions
L = {α
1
, α
2
, . . . , α
n
, α
i
∈ GF (2
m
), G(α
i
) 6= 0}.
Definition 1. [8] A binary vector a = (a
1
a
2
. . . a
n
) is a codeword of Γ (L, G)-
code if the following congruence is satisfied
n
X
i=1
a
i
1
x − α
i
≡ 0 mod G(x).
?
The research leading to these results has received funding from the Ministry of
Education and Science of the Russian Federation according to the project part of
the state funding assignment No. 2.2716.2014/, July 17th, 2014.

Definition 2. [8] The Goppa code is called a separable code if its Goppa poly-
nomial G(x) has no multiple roots.
Definition 3. [8] The separable (L, G) - code with L ⊂ GF (2
m
) and deg G(x) = t
is called a reducible one if all t roots of a polynomial G(x) belong to GF (2
m
).
The length of the code is equal to n = 2
m
− t.
Definition 4. [8] The (L, G) - code is called an irreducible one if the Goppa
polynomial G(x) is irreducible over GF (2
m
). The length of this code is equal to
n = 2
m
.
The known results on the covering radius of different classes of codes were ex-
tended in paper [9] and the upper bound of the covering radius of the irreducible
Goppa codes was presented:
R(C) ≤ 2t + 1, if 2
m
≥ 4(t − 1)
4t+2
2
1 +
q
1 −
1
(t−1)
4t
4t+2
. (1)
O.Moreno [10] in 1981 proved that, when m is odd, the irreducible binary
Goppa co des with parameters (2
m
, 2
m
− 2m, 5) are quasi-perfect and hence the
covering radius is equal to 3. Later G.L.Feng and K.K.Tzeng [11] showed that
when m is even the covering radius is 4.
In general case the lower bound of the covering radius of Goppa codes is
known for reducible separable Goppa codes only. It was proved by A. Tietavainen
[12]. He used the ”Superco de Lemma” for the proof of the lower bound of the
covering radius of reducible separable Goppa codes.
Lemma 1. (The Supercode Lemma from [1, 13]) Let C
1
and C
2
be linear codes
and C
1
⊂ C
2
. Then
R(C
1
) ≥ min {wt(x), x ∈ C
2
\ C
1
} = d(C
2
),
where d(C
2
) is the minimum distance of the code C
2
.
It is obvious that for the reducible Goppa code C
1
with
G
1
(x) =
t
Y
i=1
(x − α
j
i
), L
1
= GF (2
m
) \ {α
j
1
, α
j
2
, . . . , α
j
t
},
for example, Goppa code C
2
with
G
2
(x) =
t−1
Y
i=1
(x − α
j
i
), L
2
= L
1
can be chosen as a supercode. It means that in this case
R(C
1
) ≥ d(C
2
) ≥ 2(t − 1) + 1 = 2t − 1.

However, for the irreducible Goppa code C
1
with the Goppa polynomial G
1
(x) ∈
IF
2
m
[x] and L = GF (2
m
) the supercode C
2
with G
2
(x) =
G
1
(x)
x−β
, G
1
(β) = 0,
β ∈ GF (2
mt
), L = GF (2
m
) is the same as the code C
1
, and hence it is impossible
to use Lemma 1.
Therefore, ”The Supercode Lemma” cannot be used for constructing the
lower bound of the covering radius of irreducible Goppa codes. In general case
for any binary code, a lower bound to the covering radius of the code is R(C),
given by sphere-covering b ound :
R(C)−1
X
i=0
µ
n
i
¶
+ γ
0
µ
n
R(C)
¶
= 2
n−k
, where 0 < γ
0
≤ 1. (2)
As far as we know, the nontrivial lower bound of the covering radius of
irreducible Goppa codes has not been presented. The exhaustive algorithm for
determining the coset leader weight distribution was presented in [14] and some
results on covering radius for irreducible binary Goppa codes with lengths 32, 64
and 128 were obtained.
Below, we will prove that the lower bound of the covering radius of all binary
irreducible Goppa codes of dimension k = 2
m
− mt, t = deg G(x), L = GF (2
m
)
is defined by the following relation
R(C) ≥ 2t − 1. (3)
In Section 3 we compare new bound (3) for covering radius and results ob-
tained in [14].
2 Main result
We will use the results from [15, 16] for the proof of the lower bound of the
covering radius of all binary irreducible Goppa codes.
Let us consider a binary irreducible Goppa code C of the length n = 2
m
and
dimension k = n−mt, with the Goppa polynomial G(x) ∈ IF
2
m
[x], deg G(x) = t,
and L = GF (2
m
).
Proposition 1. (Lemma 2 from [16]) For every syndrome S
j
(x) ≡
n
P
i=1
e
j
i
1
x−α
i
mod G(x)
of a binary irreducible Goppa code C there exists its rational fraction
ϕ
0
j
(x)
ϕ
j
(x)
such
that
ϕ
0
j
(x)
ϕ
j
(x)
≡ S
j
(x) mod G(x), (4)
where ϕ
j
(x) is a separable polynomial with coefficients from GF (2
m
),
deg ϕ
j
(x) ≤ t, ϕ
0
j
(x) is a formal derivative of the polynomial ϕ
j
(x).
e = (e
1
e
2
. . . e
n
) is an error vector, wt(e) ≤ R(C).
Theorem 1. [8]
The number of normalized polynomials of the degree ` irreducible over the
field GF (2
m
) is determined by the value
I
2
m
(`) =
1
`
X
d|`
µ(d)2
m
`
d
,
where µ(d) is the M¨obius function:
µ(d) =
1 if d = 1 ;
(−1)
r
if d is a product of r different prime numbers;
0 in all other cases.
Lemma 2. [17]
The number of unitary separable polynomials of degree ` > 1 with coefficients
from the field GF (2
m
) is M
`
2
m
= 2
m`
− 2
m(`−1)
.
The number of different nonzero syndromes S
j
(x) is defined by the value
2
mt
− 1 and the number of different separable polynomials ϕ
j
(x) corresponding
to these syndromes (4) is defined by M − 1 = 2
mt
− 1. Where M is the number
of all separable polynomials from IF
2
m
[x] of degree less or equal t [15, 16] :
M = M
1
+ M
2
+ . . . + M
t
= 2
mt
,
M
1
= 2
m
,
where M
1
is the number of reducible separable polynomials
of the first degree,
M
2
= M
2
+
f
M
2
= M
2
2
m
= 2
2m
− 2
m
,
where M
2
is the numb er of reducible separable polynomials
of the second degree,
f
M
2
is the number of irreducible over GF (2
m
) p olynomials
of the second degree,
M
2
=
µ
2
m
2
¶
= 2
2m−1
− 2
m−1
,
f
M
2
= I
2
m
(2) =
2
2m
−2
m
2
,
.
.
.
M
t
= M
t
+
f
M
t
= M
t
2
m
= 2
tm
− 2
(t−1)m
,
where M
t
is the numb er of reducible separable polynomials
of degree t,
f
M
t
is the number of irreducible over GF (2
m
) p olynomials
of degree t,
f
M
t
= I
2
m
(t), M
t
= M
t
2
m
−
f
M
t
= 2
tm
− 2
(t−1)m
− I
2
m
(t).
(5)
Let us denote by T
i
the number of different coset leaders of weight i of the
code C. It is known that the following relations:
T
0
= 1, T
1
= n = 2
m
, T
2
=
µ
n
2
¶
, T
t
=
µ
n
t
¶
,
R(C)
X
i=0
T
i
= 2
n−k
are fulfilled for the code C.

Theorem 2. For the binary irreducible Goppa code C of dimension k = 2
m
−
mt , Goppa polynomial G(x), deg G(x) = t and locator set L = GF (2
m
), the
minimum weight τ of the coset leader e = (e
1
e
2
. . . e
n
) corresponding to the
syndrome
S(x) =
ϕ
0
(x)
ϕ(x)
, where ϕ(x) is the irreducible polynomial of the second degree,
satisfies the relation
τ ≥ 2t − 1.
Proof. Let us consider the syndromes S(x) satisfying the following relation:
ϕ
0
(x)
ϕ(x)
≡ S(x) mod G(x),
ϕ(x) is the irreducible polynomial, deg ϕ(x) = 2.
(6)
Let the error vector e = (e
1
e
2
. . . e
n
) be a coset leader of the code C corre-
sponding to syndrome S(x) that satisfies relation(6).
S(x) ≡
n
P
i=1
e
i
1
x−α
i
≡
σ
0
(x)
σ (x )
mod G(x), wt(e) = τ ≤ R(C),
σ(x) =
Q
e
j
6=0
(x − α
j
), deg σ(x) = τ.
Then
σ
0
(x)ϕ(x) + ϕ
0
(x)σ(x)
σ(x)ϕ(x)
≡ 0 mod G(x).
Since the formal derivative is in the numerator, the relation can be rewritten as
σ
0
(x)ϕ(x)+ϕ
0
(x)σ(x)
σ (x) ϕ(x)
≡
ω
2
(x)
ψ (x)
≡ 0 mod G(x),
ψ(x) = σ(x)ϕ(x), ω
2
(x) = ψ
0
(x).
deg ω(x) ≥ t and, therefore deg ψ
0
(x) ≥ 2t, deg ψ(x) ≥ deg ψ
0
(x) + 1 = 2t + 1.
So, τ = deg σ(x) = deg ψ(x) − deg ϕ(x) ≥ 2t − 1.
Remark 1. According to (5), there exist only
f
M
2
=
2
2m
−2
m
2
different syndromes
S(x) satisfying relation (6).
Corollary 1. The lower bound of the covering radius R(C) of the binary irre-
ducible Goppa code C of dimension k = 2
m
−mt with G(x) ∈ IF
2
m
[x], deg G(x) =
t and L = GF (2
m
) is defined by the inequality
R(C) ≥ τ ≥ 2t − 1.
Corollary 2. The lower bound of the number of coset leaders of the code C,
with the weight not less than 2t − 1 is defined by the number
f
M
2
of different
syndromes S(x) satisfying relation (6):
R(C)
X
i=2t−1
T
i
≥
f
M
2
=
2
2m
− 2
m
2
.
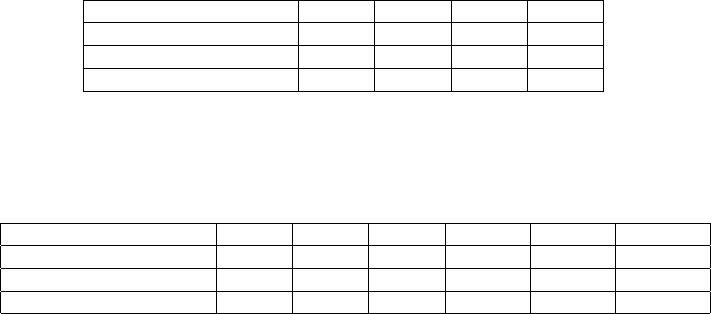
3 Examples
As examples we present Table 1 and Table 2 showing the values of the covering
radius results for irreducible binary Goppa codes that were obtained in [14] by
using algorithm to evaluate the coset leader weight distribution, sphere-covering
bound (2) and new lower bound of covering radius (3) for some binary codes
described in [14].
Table 1. The covering radius of (32, k) irreducible binary Goppa codes.
Goppa code (n, k, d) (32,22,5) (32,17,7) (32,11,9) (32,6,11)
covering radius [14] 3 6 8 12
new lower bound (3) 3 5 7 9
sphere-covering bound (2) 3 4 6 7
Table 2. The covering radius of (64, k) and (128, 93) irreducible binary Goppa codes.
Goppa code (n, k, d) (64,52,5) (64,46,7) (64,40,9) (64,34,11) (64,28,13) (128,93,11)
covering radius [14] 4 5 7 9 12 9
new lower bound (3) 3 5 7 9 11 9
sphere-covering bound (2) 3 4 6 8 10 7
4 Conclusion
The lower bound of the covering radius of binary irreducible Goppa codes with
the Goppa polynomial of degree t and L = GF (2
m
) is obtained:
R(C) ≥ τ ≥ 2t − 1 if the code dimension is k = 2
m
− mt.
It should be mentioned that to establish the bound it was convenient to adopt
the method that we had used for designing the class of binary Goppa codes that
are perfect in the weighted Hamming metric [15, 16].
5 Acknowledgments
The authors would like to thank the reviewers for comments and fruitful sug-
gestions which helped to improve the presentation of this paper.
References
1. Cohen, G.D., Karpovsky, M.G., Mattson, H.F.,Jr., Schatz, J.R.: Covering radius
survey and recent results, IEEE Trans. Inform. Theory, 31 , 328-343 (1985).
2. Cohen, G.D.,Lobstein, A.C., Sloane, N.J.A.: Further Results of the Covering radius
of codes, IEEE Trans. Inform. Theory ,32 , 680-694 (1986).
3. Vladuts, S. G., Skorobogatov, A. N.: Covering radius for long BCH codes, Problemy
Peredachi lnlormatsii, vol. 25, 38-45 (1989). Translated in: Problems of Inform.
Transm., vol. 25, No. 1, 28-34 (1989).
4. Moreno, C. J. , Moreno, O.: Exponential sums and Goppa codes I, Proc. American
Math. Sac., vol. 111, 523-531 (1991).
5. Cohen, G.D., Litsyn, S.N., Lobstein, A.C., Mattson, H.F., Jr.: Covering radius
1985 1994, Appl. Algebra Eng. Comm. Comp., 8 , 173-239 (1997).
6. Cohen, G., Honkala, I., Litsyn, S., Lobstein, A.: Covering codes. North-Holland,
Amsterdam (1997).
7. Goppa, V.D.: A new class of linear error correcting codes, Probl. Inform.Transm.
vol.6, no.3, 24-30 (1970).
8. MacWilliams, F.J., Sloane, N.J.A.: The Theory of Error-Correcting Codes. Ams-
terdam, Netherlands, North-Holland (1977).
9. Levy-dit-Vehel, F., Litsyn, S.: Parameters of Goppa codes revisited, IEEE Trans.
Inform. Theory, 1811-1819 (1997).
10. Moreno, O.: Goppa codes related quasi-perfect double-error-correcting codes, in
”Abstracts of Papers,” IEEE Internat. Sympos. Inform. Theory, Santa Monica,
Calif.,(1981).
11. Feng,G.L., Tzeng, K.K.: On Quasi-perfect property of double-error-correcting
Goppa codes and their complete decoding, Information and Control, 61, 132-146
(1984).
12. Tietavainen,A.: Codes and character sums ,Lecture Notes in Computer Science
388, Codes theory and Applications, 3-12 (1987).
13. Cohen, G., Frankl, P.: Good coverings of Hamming spaces with spheres, Discrete
Mathematics, 56, 125-131 (1985).
14. Grassl,M.,Tomlinson, M. , Tjhai, C.J., Jibril,M., Ahmed, M.Z.:Results On The
Covering Radius Of Some Best Known Binary Codes,(unpublished)
15. Bezzateev, S.V., Shekhunova, N.A.: Class of binary generalized Goppa codes p er-
fect in weighted Hamming metric, Proc. of WCC-2011, Paris, 233-242 (2011).
16. Bezzateev, S., Shekhunova, N.: Class of generalized Goppa co des perfect in
weighted Hamming metric, Designs, Codes and Cryptography, v.66, n.1-3, 391-
399 (2013).
17. Carlitz L.: The arithmetic of polynomials in a Galois field. Am. J. Math. 54, 39-50
(1932).
