
Population projection
Ernesto F. L. Amaral
October 15–29, 2019
Demographic Methods (SOCI 320)

Population projection
• Transition matrices
• Structural zeros
• The Leslie matrix subdiagonal
• The Leslie matrix first row
• Projecting fillies, mares, seniors
2

Transition matrices
• Transition matrices are tables used for population
projection
• Official presentations of projections are often
filled with disclaimers cautioning the reader that
projections are not predictions
– They do not tell us what the world will be like but only
what the world would be like if a particular set of
stated assumptions about future vital rates turned out
to be true
• The assumptions may or may not bear any
relation to what actually happens
3

Disingenuous disclaimers
• Projection is not just a game with computers and
pieces of paper
• We do projections for a purpose to foresee the
future of the population
• The choice of credible assumptions about vital
rates is an important part of the art and science of
projection
– As are the formulas we use to implement the
calculations
– In this chapter, we concentrate on the formulas
4

Previous failures
• The record of demographers at guessing future
vital rates has not been good
• The community failed to predict
– The Baby Boom of the 1950s and 1960s
– The Baby Lull of the 1970s and 1980s
– It largely failed to predict the continuing trend toward
lower mortality at older ages in industrialized countries
• We do not yet understand the mechanisms that
drive demographic change
– We need deeper theories with better predictive power
5

But we are doing good
• Despite these failures with previous predictions,
demographers do better than economists,
seismologists...
• Choice of assumptions about future fertility,
mortality, marriage, divorce, and immigration may
be difficult
• But methods for using those assumptions to
calculate future population sizes and age
distributions are well developed and satisfactory
6

Focus of this chapter
• We study these methods of calculation
• Tools based on matrices and vectors
• Projection over discrete steps of time
• Populations split up into discrete age groups
7

Several characteristics
• Sophisticated projections can treat a population
classified by many characteristics
– Sex, age, race, ethnicity, education, marital status,
income, locality
– So much detail is not common
• Progress is being made, under a European team
led by the demographer Wolfgang Lutz
– Incorporating education into worldwide projections
8

Basic ideas: simple case
• The basic ideas are illustrated by simple
projections
• Focus on a single sex
• All races and ethnicities together
• We subdivide the population only by age
9

Leslie matrices
• The main tools for projecting the size and age
distribution of a population forward through time
are tables called “Leslie matrices”
– By P.H. Leslie (1945)
– Same approach done few years earlier by H.
Bernardelli and E.G. Lewis
• Related to Markov chains in probability theory
– But what is being projected with Leslie matrices are
expected numbers of individuals rather than
probabilities
10

Leslie matrices for age structure
• Leslie matrices are a special case of transition
matrices
• Demographers use general transition matrices
– To project a distribution of marital status, parity,
education, or other variables into the future
• They use the special transition matrices that
Leslie defined
– To project age structure
11

Defining a transition matrix
• A transition matrix is a table with rows and
columns showing the expected number of
individuals
– who end up in the state with the label on the row
– per individual at the start in the state with the label on
the column
12

One-step transition
• A Leslie matrix is a special case of a transition
matrix in which the states correspond to age
groups
– Processes of transition are surviving and giving birth
• The Leslie matrix describes a one-step transition
– We project the population forward one step at a time
– The time between start and end (projection step)
should be equal to the width (n) of all age groups
13

Age group width
• The fact that the step size has to equal the age
group width is crucial
– Generally pick one sex, usually females
– Divide the female population into age groups of width n
– Width may be 1, 5, 15 years, or some other number
14

Examples
• If we are using 1-year age groups
– We have to project forward 1 year at a time
– To project 10 years into the future requires 10
projection steps
• If we are using 5-year age groups
– We have to project forward 5 years at a time
– To project 10 years into the future requires only 2
projection steps
15

Closed population
• We assume a closed population
• No migrants are included in projections
• People enter the population only by being born to
members already in the population
• People leave it only by dying
16

Childbirth as a transition
• Projections treat childbirth as a possible transition
along with survival
– People who end up in some state may not be the same
people who start in any one of the states
– They may be the babies of people who start in the
various states
• We are concerned with the expected numbers
– In the state for the row (end)
– Per person in the state for the column (start)
– Without regard to how the people are channeled there
17


Structural zeros
• The logic of the transition process is built into a
transition matrix through the pattern of zeros
• Some age groups owe no part of their numbers at
the end of the step to certain other age groups
• Suppose we have n=5
– We have 5-year-wide age groups
– We are projecting forward 5 years in one step
19

Example of teenagers
• No teenagers owe their numbers to 40-year-olds
five years before
• The value of the Leslie matrix element has to be
zero in
– The row for 15 to 20-year-olds (end)
– The column for 40-year-olds (start)
• This is a “structural zero”
– We know because of the logic of the processes of
aging and childbirth
20

Example of a Leslie matrix
• Most of the elements of a Leslie matrix are
structural zeros
– We can fill them in immediately
– At the end of 5 years, people age up to 5 years
– No one can get younger over time
21
End
Start

Following the same logic
• Below the first row, all elements are structural
zeros except the subdiagonal
• No one can
– Jump an age group
– Stay in the same age group
– Get younger
• They can only move into the next age group
– If they survive
– It is important to have the same age-group width
22

First row
• What about the first row, for people who end up
aged 0 to 5 at the end of 5 years?
– No one can survive into this row
– These elements are not structural zeros
– There can be babies born during the projection step
who are found in this age group at the end of the step
– The number of babies depends on the number of
potential parents in the various age groups at the start
23

First row of a Leslie matrix
24
Babies
at the end
Potential parents at the start

Upper-left element
• The upper-left element equals zero depending on
the age-group width
– If n=5, we do not expect there to be any babies in 5
years to people 0 to 5 at the start
– If n=15, we do expect babies in the next 15 years to
people aged 0 to 15 at the start
• This element also depends on empirical
knowledge about youngest ages of childbearing
– It is often equal to zero
– But it is not regarded as a structural zero
25

Representing structural zeros
• Another way of representing information about
structural zeros is a diagram of permitted
transitions
• We mark states within circles and draw an arrow
from one state to another if there is a nonzero
element for that column-row pair
– Show links from individuals in the sender state at the
beginning of the arrow
– To individuals who can show up in the receiver state at
the end of the arrow
26

Arrow diagrams
• Arrow diagrams are helpful when transitions are
not between age groups
• Useful for transitions between states with a logic
of their own
• Same idea as programmer flow charts
27
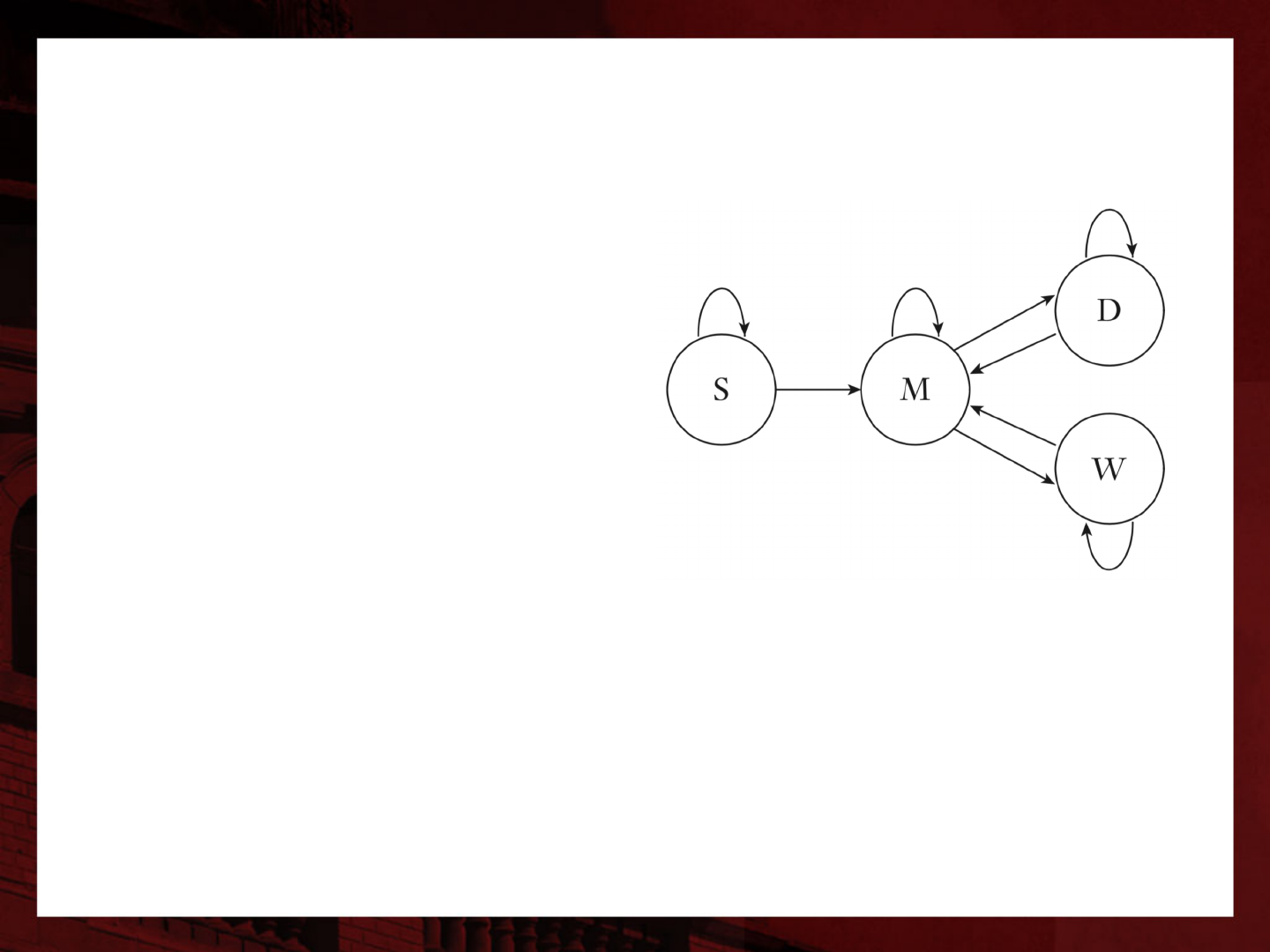
Example for marital status
• Four states
– Single (S), never married
– Married (M)
– Widowed (W)
– Divorced (D)
• Suppose the projection step is too short
– Nobody can get both married and divorced, or both
divorced and remarried within a single step
– Multiple transitions within one step are not numerically
significant
28

Marital status transition matrix
• The structural zeros in the transition matrix
corresponding to the previous diagram appear in
slots marked “0”
29


The Leslie matrix subdiagonal
• We generally denote a matrix by a single capital
letter like A
– The first subscript is for the row and the second
subscript is for the column
– A
3 2
element in third row and second column, survivors
from the second age group to the third age group
• This notation for matrix elements is universal
– A
to, from
or A
row, column
– Subscript for the destination age group comes first
– Subscript for the origin age group comes second
31

Developing a formula
• Develop a formula for the elements along the
subdiagonal of the Leslie matrix
– They represent transitions of survival
– Continue to use 5-year-wide age groups
32
End
Start

Example
• Consider A
3 2
, the expected number of people
– Aged 10 to 15 at the end (row)
– Per person aged 5 to 10 at the start (column)
• Age group of 5-to-10-year-olds at the start, at
time t (“today”)
– Composed of cohorts born between times t−10 and t−5
• We follow the experience of five 1-year birth
cohorts on the Lexis diagram...
33
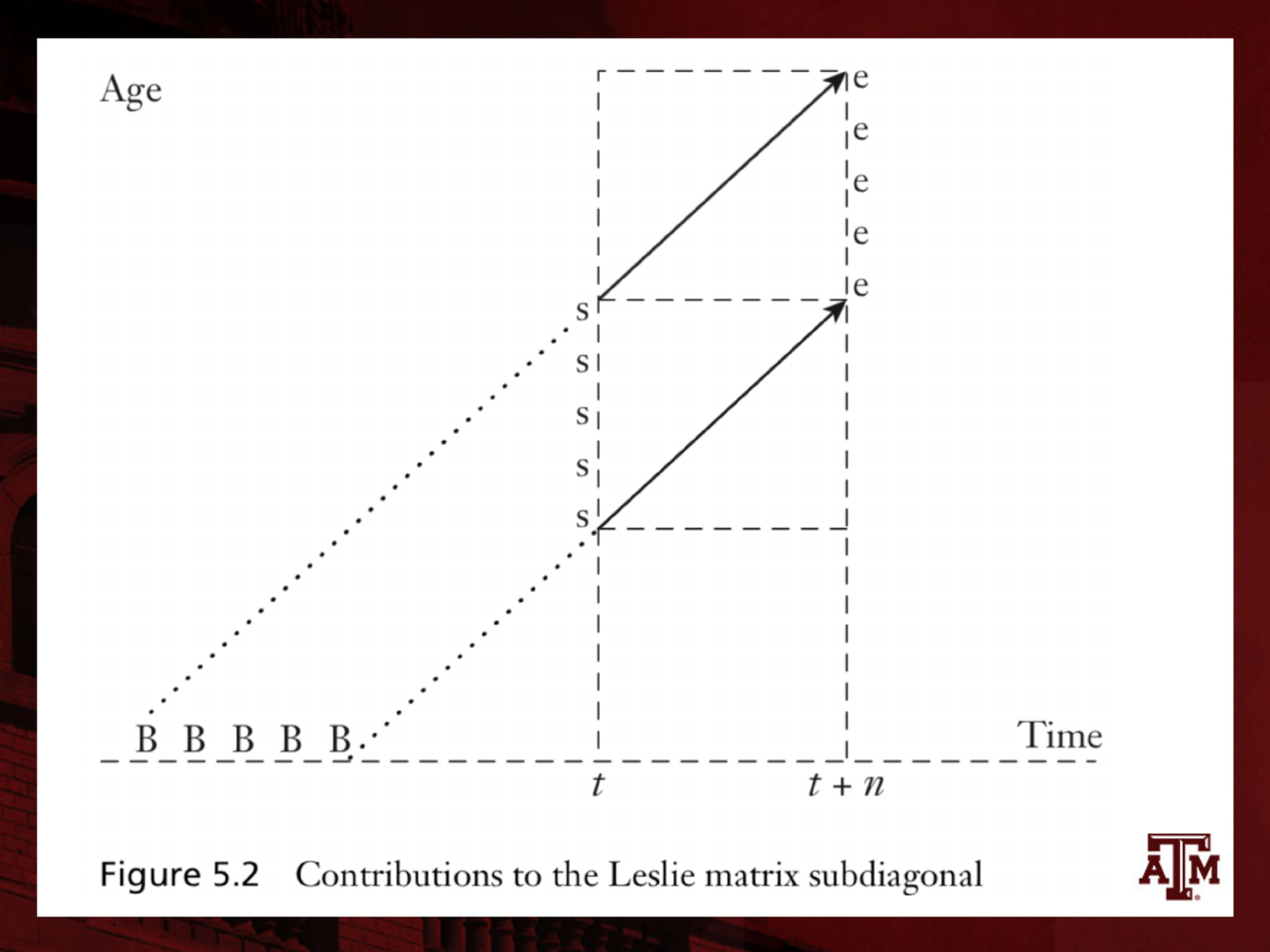
34

Symbols
• “B” symbols represent single-year cohorts at birth
• “s” symbols represent cohorts at the start of the
projection step
– 5–10 age group
• “e” symbols represent cohorts at the end of the
projection step
– 10–15 age group
35

Assumptions
• We ignore changes in sizes of cohorts at birth
inside each 5-year period
– We pretend that all changes in initial cohort sizes occur
in jumps between periods
• We also assume that the same lifetable
(mortality)
– Applies to all the 1-year cohorts in this 5-year group of
cohorts
• From 5–10 age group to 10–15 age group
36

Cohorts in the diagram
• Examples of some of the cohorts on the diagram
• The earliest/oldest cohort (now 10-year-olds)
– They had some size l
0
at birth
– At the start of the projection step (s), l
10
members left
– At the end of the projection step (e), l
15
members left
• The latest/youngest cohort (now 5-year-olds)
– They had the same size l
0
at birth
– Now (s), l
5
members left
– Five years from now (e), l
10
members left
37

Size of 5-year age group
• The whole 5-year age group is about five times
as large as the average size of its youngest and
oldest cohorts
• At the start of the projection step (s): t
(5/2) (l
5
+ l
10
)
• At the end of the projection step (e): t + n
(5/2) (l
10
+ l
15
)
38

Person-years lived
• The sizes of the 5-year age group at the start and
end are approximations for person-years lived
5
L
5
= (5/2) (l
5
+ l
10
)
5
L
10
= (5/2) (l
10
+ l
15
)
• If the age group was split into many small cohorts
– We could add them all up
– We would have obtained the
n
L
x
values exactly
39

Subdiagonal as ratios
• The subdiagonal element A
3 2
of the Leslie matrix
– Ratio of the 10–15-year-olds at the end
– To the 5–10-year-olds at the start
40

Ratio of L values
• Each subdiagonal element of a Leslie matrix is a
ratio of big-L values
– The age label on the numerator comes from the row
– The age label on the denominator comes from the
column
41

General notation
• The bottom age (denominator) of the age group x
is expressed as x = jn − n
– In terms of the column number j
• A
3 2
: from 5–10 (denominator) to 10–15 (numerator)
– x = jn – n = 2(5) – 5 = 10 – 5 = 5
42

Different cohorts
• The cohort born between t–x–n and t–x supplies
the numerator and denominator in this element
n
L
x+n
/
n
L
x
• There is a different cohort for each age group x
– L values for different columns of the Leslie matrix are L
values from different cohort lifetables
– They are L values from a period lifetable (chapter 7)
43

Period lifetable
• Period lifetable puts together survival experience
for different cohorts as they move through the
same time period
• The Leslie matrix does the same
• At this stage, the key concept is the way that
ratios of big-L values supply elements for the
subdiagonal matrix
44


The Leslie matrix first row
• Outside the subdiagonal, the only elements in a
Leslie matrix which are not structural zeros are in
the first row
• These are the elements that take account of
population renewal
– Babies are born to parents
– They survive and counted at the end of projection step
• Formulas for the first row are more complicated
than those for the subdiagonal
– Let’s develop them one step at a time
46

Projecting female population
• Formulas are shown to project female population
– Daughters are in first row, instead of sons and
daughters
– In projections, we must have the same kinds of people
coming out as going in
• Joint projections for males and females are
possible in principle
– Simple and appealing two-sex model is a problem that
remains largely unsolved
47

Projecting male population
• One-sex projections could be done for males
– Inserting fertility rates for sons and fathers
– But motherhood ages are more regular than
fatherhood ages
• Usually the female population is projected
– Counts of males are estimated from projected counts
for females
48

Fraction female at birth
• When projecting females, we must remember
that we need fertility rates for daughters only
• Published fertility rates are usually for babies of
both sexes
• Need to multiply by the fraction female at birth
(f
fab
)
– By our default, it is the fraction 0.4886
49

Full formula for first row
• Formula for the expected number of daughters
aged 0 to n at the end of the projection step
– Per woman aged x to x+n at the start
• We write j(x) for the corresponding column with
x=j(x)(n)−n
50

Formula step by step
• A
1, j(x)
pertains to
– Daughters entering the population over n years
– By being born to mothers aged x to x+n at the
start
51
Daughters
at the end
(0 to n)
Potential mothers at the start (x to x+n)

Crude version of formula
• How many daughters per potential mother should
there be?
• A first guess would be to multiply
– The daughters-only age-specific fertility rate (
n
F
x
)(f
fab
)
for women x to x+n
– By the years at risk in the interval (n)
•
n
F
x
indicates period age-specific fertility rate
– Instead of small
n
f
x
for cohort age-specific fertility rate
• It provides a first crude version of the formula
(n)(
n
F
x
)(f
fab
)
52

Consider mortality of daughters
• Need to recognize that not all baby daughters
survive to the end of the projection interval
– The first age group counts kids aged 0 to n at the end
of the step, not newborns
– Need to estimate proportion of babies born during the
n years who survive to be counted
– Babies born early in the period have to survive to be
nearly n years old
– Babies born late in the period have to survive only a
little while
53
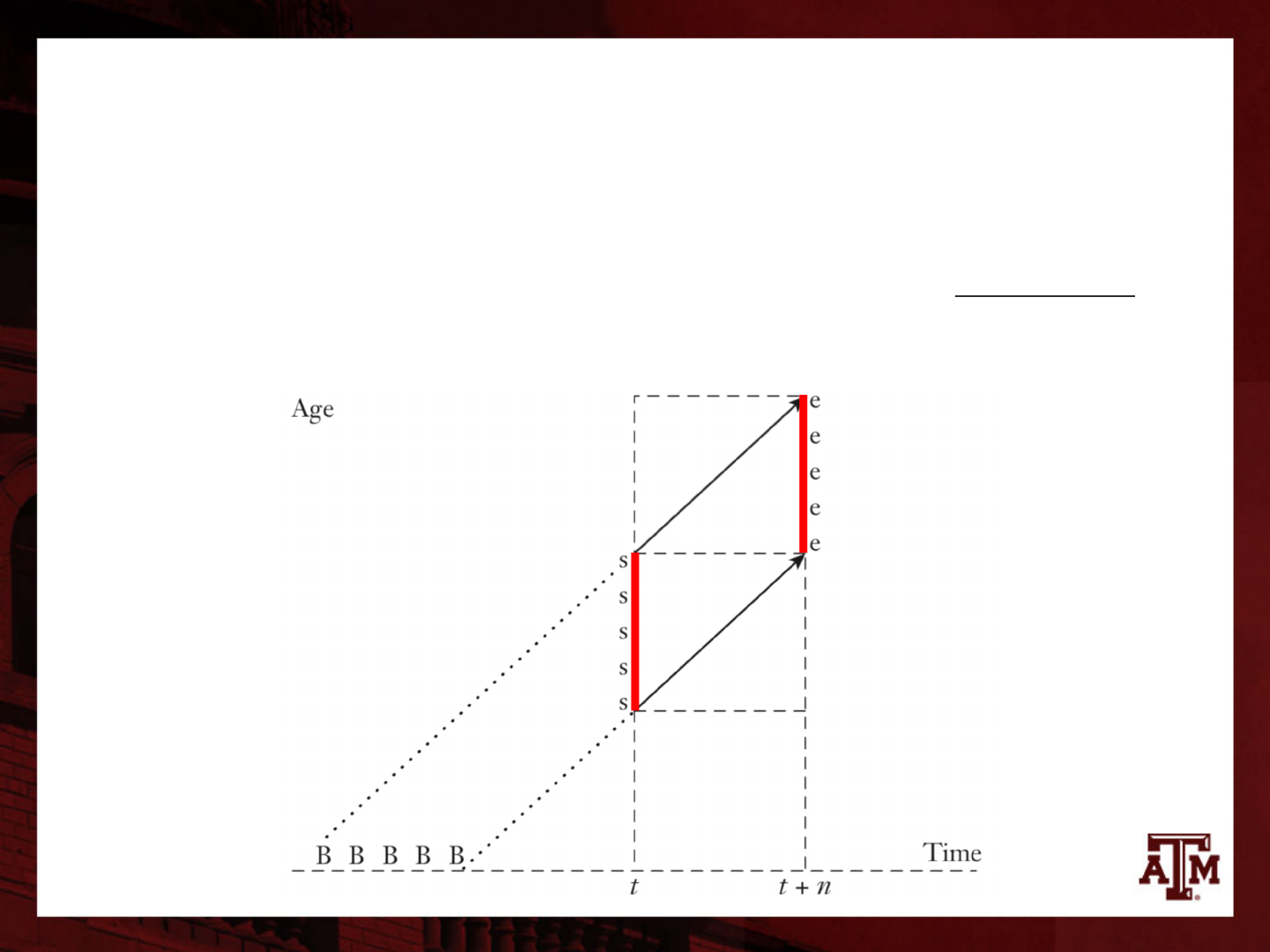
Survivorship for subdiagonal
• We averaged survivorships when we were finding
a formula for subdiagonal elements of mothers
– Compare lifelines crossing two sides of parallelogram
54
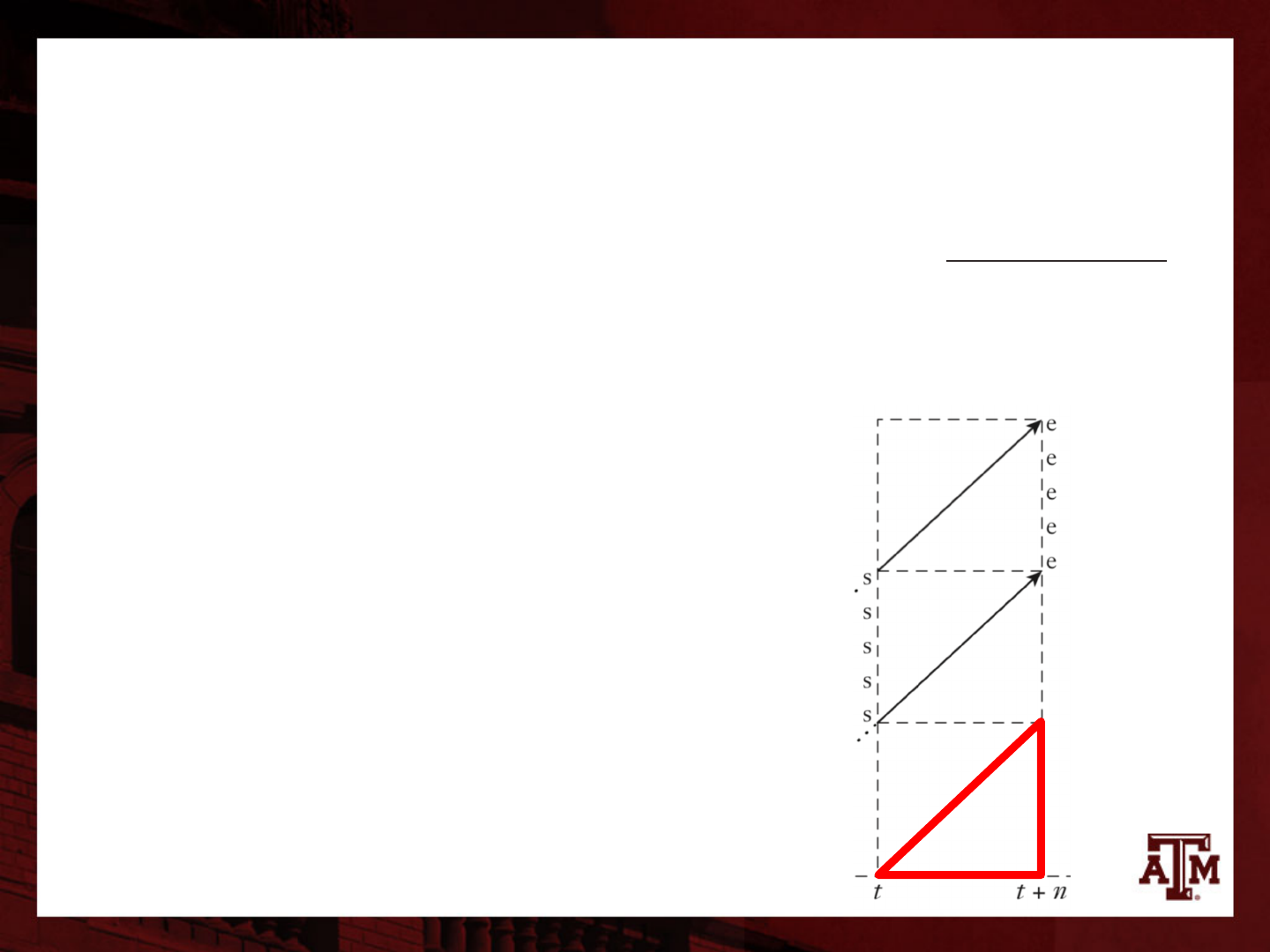
Survivorship for newborns
• We need average of survivorships for daughters
– They start at birth, bottom axis of the Lexis diagram
– Compare lifelines crossing two adjacent sides of a
right triangle
55
– Triangle base covers the interval
from t to t+n
– Perpendicular side reaches up
from age 0 to age n above time
t+n

Average of survivor daughters
• We ignore changes in initial cohort size within the
interval
– Out of any l
0
girls born near the start of the interval,
about l
n
survive to the end
– Out of any l
0
born close to the end, nearly all l
0
survive
to the end
• From (n)(l
0
) births, we expect this average of
daughters who survive
– (n)(l
n
+ l
0
) / 2
– This is a standard approximation for
n
L
0
56

Better version of formula
• Average of daughters who survive:
n
L
0
= (n)(l
n
+l
0
)/2
• Total births: (n)(l
0
)
• Ratio of survivors to births:
n
L
0
/ (n)(l
0
)
• Multiply this ratio by the first crude formula
57
Crude formula
Mortality
of daughters
n terms will cancel out

Consider aging of mothers
• Consider the aging of potential mothers during
the projection interval
– Women aged x to x+n at the start only spend on
average about half of the next n years in their starting
age group
– They grow older and spend about half the interval in
the next age group
• In place of n years at
n
F
x
: (n)(
n
F
x
)
– We have about n/2 years at
n
F
x
: (n/2)(
n
F
x
)
– We have about n/2 years at
n
F
x+n
: (n/2)(
n
F
x+n
)
58

Consider mortality of mothers
• n/2 and n/2 are not quite the right breakdown
– Not all women survive into the next age group
• We pretend that all deaths between start (s) and
end (e) happen at the age-group boundary at
age x+n
59
– Then fraction of women surviving into the
next age group is
n
L
x+n
divided by
n
L
x
– It reduces time spent in the older age group
(
n
F
x+n
) by this survival fraction (
n
L
x+n
/
n
L
x
)

Aging and mortality of mothers
• Consider aging of mothers
– Years spent in starting and ending age groups (n/2)
• Consider mortality of mothers
– Reduce time spent in the older age group (
n
F
x+n
) by
this survival fraction (
n
L
x+n
/
n
L
x
)
60

All elements of formula
61
Aging
of mothers
Mortality
of daughters
Mortality
of mothers
Only
daughters
!
2
Women live half of the time
in starting and next age groups

All elements of formula
62
Aging
of mothers
Mortality
of daughters
Mortality
of mothers
Only
daughters
!
2
Women live half of the time
in starting and next age groups

All elements of formula
63
Aging
of mothers
Mortality
of daughters
Mortality
of mothers
Only
daughters
!
2
Women live half of the time
in starting and next age groups

Fertility of youngest age group
• Usually the interval width (n) is 1 or 5 years
– Age-specific fertility for the youngest age group from 0
to n will be zero
• The youngest age group is part of the
“preprocreative span”
– Period prior to procreation (production of infants)
• With wider intervals (10, 15, 20...), fertility for the
youngest age group will not equal zero
64

Correction for youngest group
• With wider intervals (10, 15, 20...)
– Children born during the projection step could grow up
and bear their own children during one projection step
• Formulas made no allowance for grandchildren
– A rough correction is to insert (2)(
n
F
0
), instead of
n
F
0
for the upper-left element of the Leslie matrix
– When fertility before age n is zero, this change has no
effect
– When it is not zero, the correction improves accuracy
65


Projecting fillies, mares, seniors
• Example of a Leslie matrix and a population
projection employing this matrix
– No more than three rows and columns
– Retain familiar 5-year age group
• Population of horses in a stable, with rates of
survival and fertility that are stylized but credible
– Fillies: young female horses (0–5)
– Mares: mature females (5–10)
– Seniors (10–15)
67

Age of reproduction
• Horses mature fairly quickly and may live to ages
like 30
• In our stable they only give birth to offspring
(foals) between ages 5–15
• We only project the population up to age 15
– Leslie matrices often stop at the last age of
reproduction
– Sizes of older age groups can be computed directly
from the relevant lifetable
68

Data for this example
• Age-specific fertility rates are
5
F
0
f
fab
= 0.000
5
F
5
f
fab
= 0.400
5
F
10
f
fab
= 0.300
• Number of survivors to specific age
l
0
= 1.000
l
5
= 0.900
l
10
= 0.600
l
15
= 0.000
69

Three parts to complete
• We have three parts of the Leslie matrix to fill in
– Structural zeros
– Subdiagonal elements
– First row
70
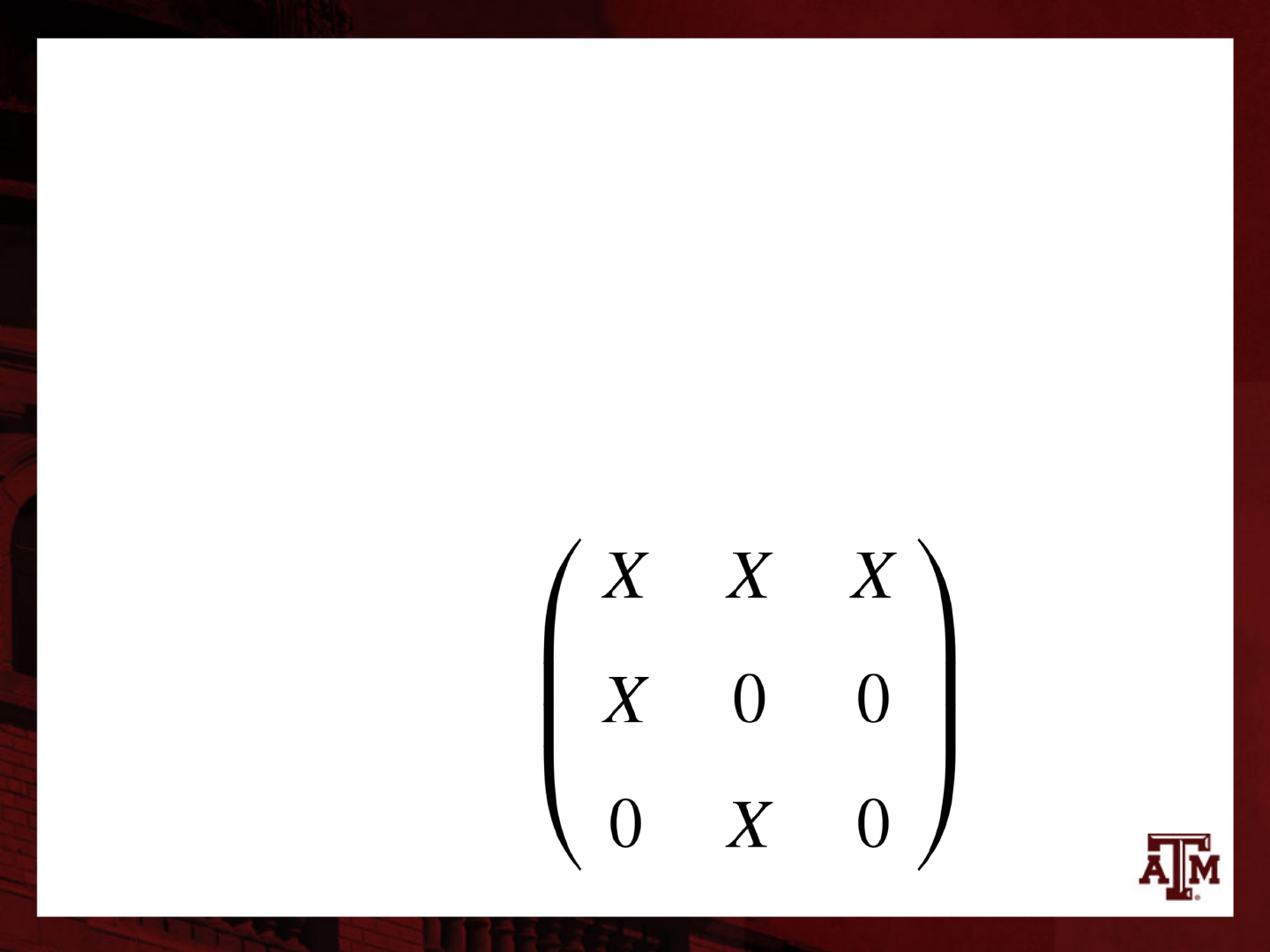
Structural zeros
• The first step in writing down the Leslie matrix is
to fill in the structural zeros
– Number 0 go on the structural zeros
• Crosses for nonzero elements go on
– Subdiagonal
– First row
71
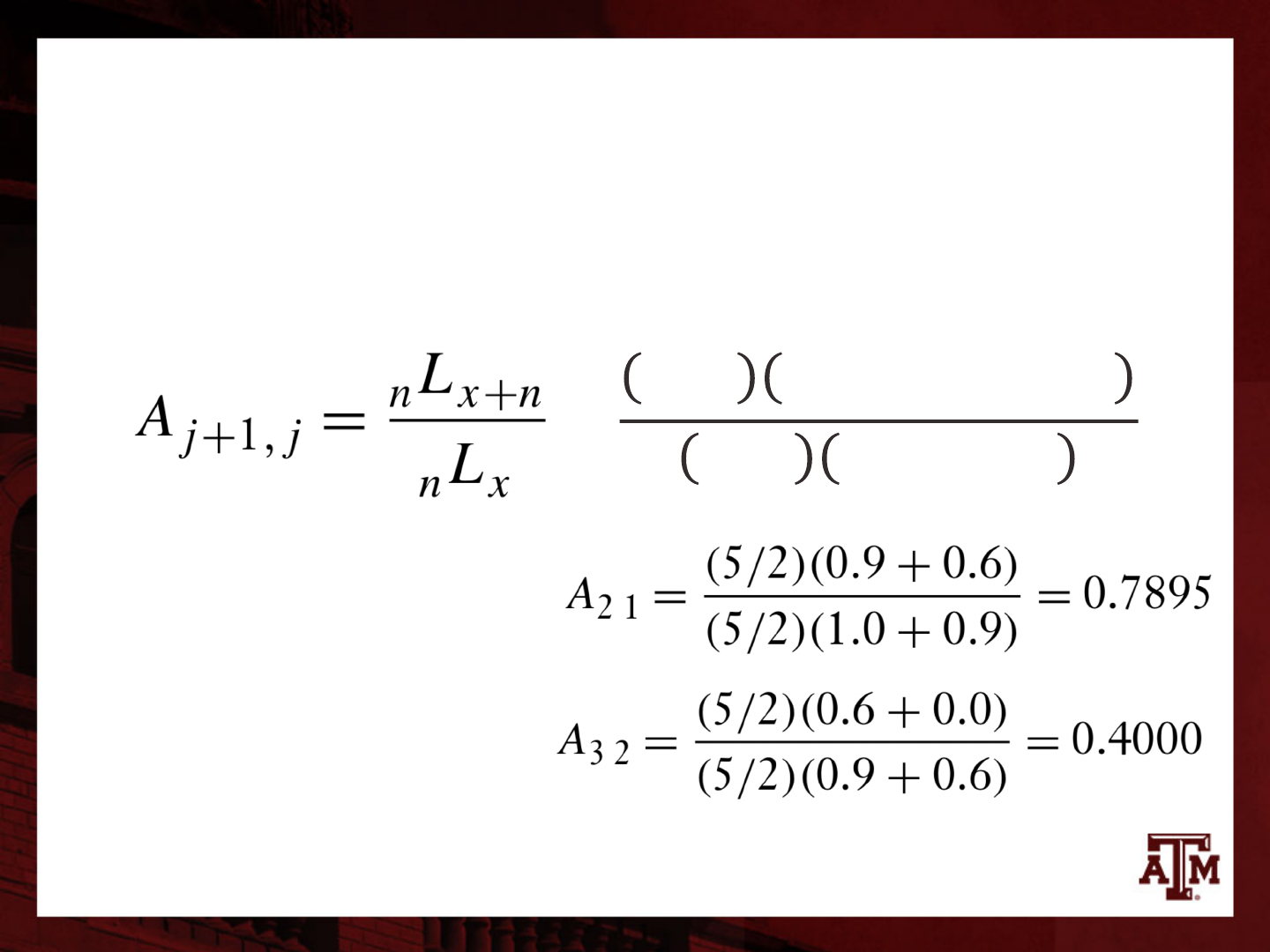
Subdiagonal
• Our second step is to compute survivorship ratios
for the subdiagonal
72
=
⁄
5 2 %
&'(
+ %
&'('(
⁄
5 2 %
&
+ %
&'(
l
0
= 1.000
l
5
= 0.900
l
10
= 0.600
l
15
= 0.000
Age group 0–5:
Age group 5–10:

First row
73
5
F
0
f
fab
= 0.000
5
F
5
f
fab
= 0.400
5
F
10
f
fab
= 0.300
5
L
0
= (5/2) (l
0
+l
5
) = (5/2) (1+0.9) = 4.75
5
L
5
= (5/2) (l
5
+l
10
) = (5/2) (0.9+0.6) = 3.75
5
L
10
= (5/2) (l
10
+l
15
) = (5/2) (0.6+0.0) = 1.50
Age group 0–5:
Age group 5–10:
Age group 10–15:

Leslie matrix for this example
74

Use matrix for projection
• Suppose at time t=0, we have
– Zero fillies (0–5)
– Four mares (5–10)
– Two seniors (10–15)
• How many fillies, mares, and seniors should we
expect after 5 years?
75
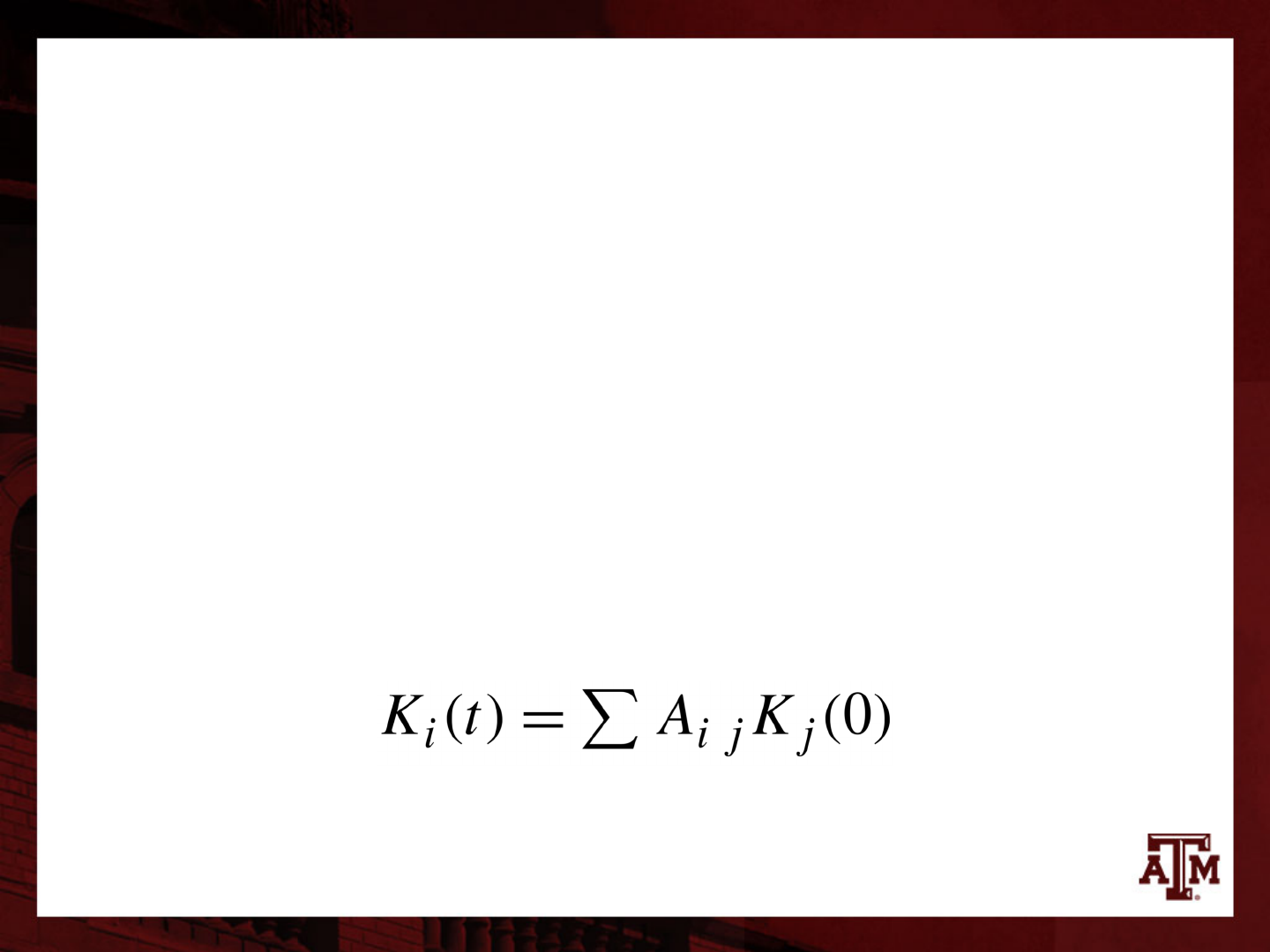
Rule for matrix multiplication
• If we write our population counts at time t as a
vector K(t), then we apply the standard rule for
matrix multiplication
– Expected population at time t (vector K(t)) equals the
product of matrix A times vector K(0)
• The general rule for matrix products says that
K(t) = A K(0) , which means...
– Summing over columns j of the matrix and elements j
of the vector
76

How many fillies (0–5)?
• First row informs number of fillies to expect at the end of
the 5-year step per horse at the start
0 + 4.94 + 1.425 = 6.365 fillies
• We should expect six or seven fillies
– Around 1/3 chance of having 7 horses
– Around 2/3 chance of having 6 horses
77

How many mares (5–10)?
• Use the second row of our matrix
• We go across the columns as we go down the starting
vector K(0)
– Zero starting fillies, four starting mares, two starting seniors
• We multiply and add up
0 mares
78

How many seniors (10–15)?
• Use the third row of our matrix
• We go across the columns as we go down the starting
vector K(0)
– Zero starting fillies, four starting mares, two starting seniors
• We multiply and add up
1.6 seniors
79

Summary
80
Leslie matrix = matrix A K(0)K(t)
• Equation for population projection
K(t) = A K(0)
• Matrices

Matrix notation
• Matrix notation makes it easy to see what
happens next
K(10) = AK(5) = AAK(0)
• AA = A
2
is not ordinary multiplication but matrix
multiplication
• In general
K(nk) = A
k
K(0)
81

Comparing to previous equation
• Equation from crude model of exponential growth
K(T) = A
T
K(0)
– It has ordinary numbers rather than vector
– It does not account for age
• New equation for population projection
K(nk) = A
k
K(0)
– It utilizes matrices and vectors, which consider age
– Same form as before, but new and richer interpretation
– This is the generalization to age-structured populations
of the Crude Rate Model, but it is still a closed
population (no migration)
82

References
Wachter KW. 2014. Essential Demographic Methods.
Cambridge: Harvard University Press. Chapter 5 (pp. 98–
124).
83

